E = 0 at all points on the spherical surface.

A charge Q is enclosed by a Gaussian spherical surface of radius R, If the radius is doubled, then the outward electric flux will
Abe reduced to half
Bremains the same
Cbe doubled
Dincreases four times
A charge $Q$ is enclosed by a Gaussian spherical surface of radius $R$ . If the radius is doubled, then the outward electric flux will
Abe reduced to half
Bremain the same
Cbe doubled
Dincrease four times
Assertion: Four point charges $q_{1}, q_{2}, q_{3}$ and $q_{4}$ are as shown in Fig,The flux over the shown Gaussians surface depends only on charges $q_{1}$ and $q_{2}$
Reason:Electric field at all points on Gaussians surface depends on any charges $q_{1}$ and $q_{2}$

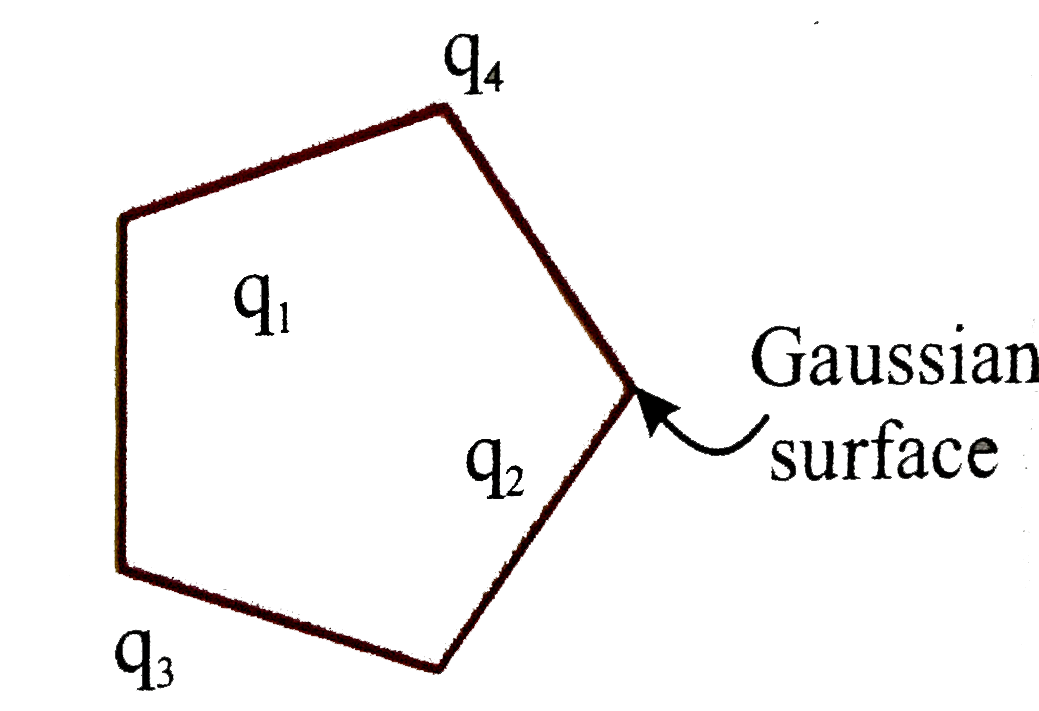ABoth $(A)$ and $(R)$ are true and $' R'$ is the correct explanation of $A$ .
BBoth $A$ and $R$ are true and $R$ is not the correct explanation of $A$
C $(A)$ is true but $(R)$ is false
D $(A)$ is false but $(R)$ is true

Consider a Gaussian spherical surface covering a dipole of charge q and -q, then