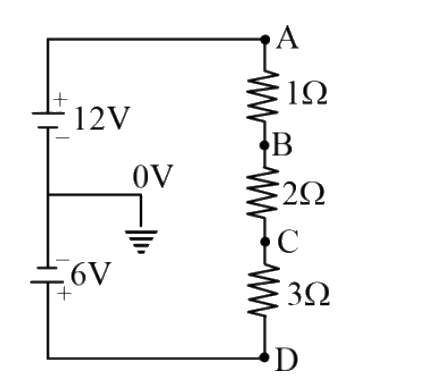
A right circular imaginary cone is shown in figure A, B, and C are the points in the plane containing the base of the cone, while D is the point at the vertex of the cone. If ϕA,ϕB,ϕCandϕD represent the fulx through the curved surface of the cone when a point charge Q is at points A, B, C, and D. respectively. then.
A
ϕA=ϕC≠0
B
ϕD≠0
C
ϕB=Q2ε0
D
ϕA=ϕC=ϕD=0
Video Solution
Text Solution
The correct Answer is:C, D
Flux through curved surface will be zero when charge is placed at A,C,orD. When charge is placed at B, flux through curved surface will be Q/2ε0.
|
Topper's Solved these Questions
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICSChapter:ELECTRIC FLUX AND GAUSS LAWExercise:Comprehension
Explore 36 Videos
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICSChapter:ELECTRIC FLUX AND GAUSS LAWExercise:Subjective type
Explore 7 Videos
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICSChapter:ELECTRIC FLUX AND GAUSS LAWExercise:Single Correct
Explore 40 Videos
- ELECTRIC CURRENT AND CIRCUITBook:CENGAGE PHYSICSChapter:ELECTRIC CURRENT AND CIRCUITExercise:Interger
Explore 8 Videos
- ELECTRIC POTENTIALBook:CENGAGE PHYSICSChapter:ELECTRIC POTENTIALExercise:DPP 3.5
Explore 14 Videos
Similar Questions
Knowledge Check
In the circuit diagram shown in figure, the potentials of the points B, C and D are respectively.
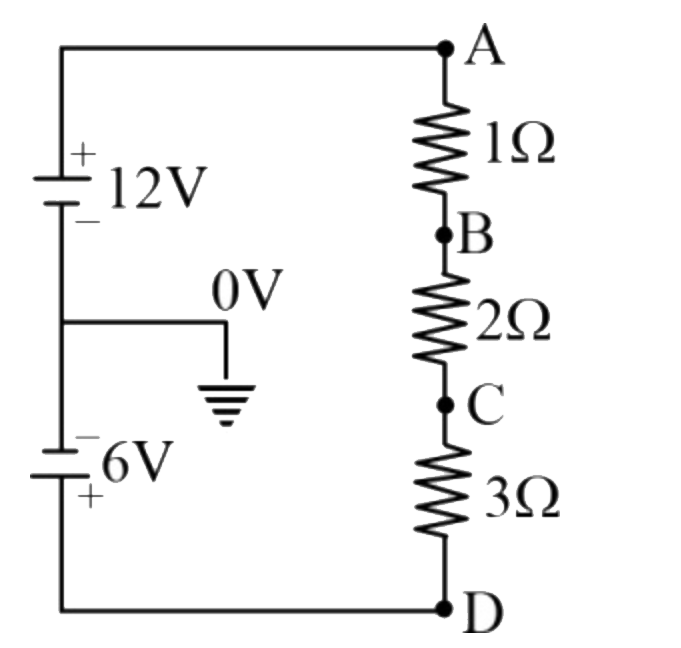 A12V,10V,6VB11V,9V,6VC11V,9V,0VD12V,10V,0V
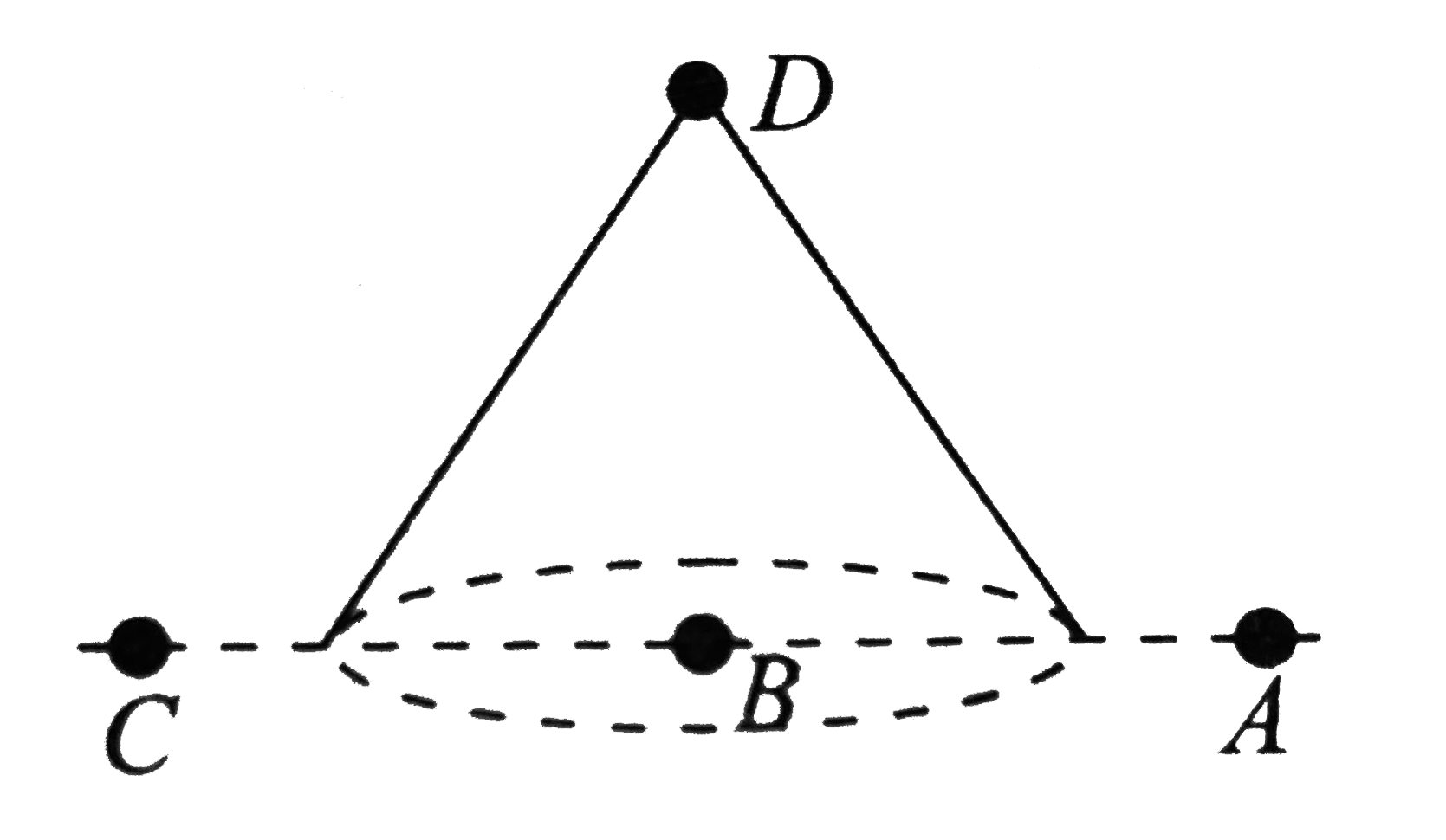
A12V,10V,6VB11V,9V,6VC11V,9V,0VD12V,10V,0VA sheet of semi circular paper (radius R) is turned around the centre in to a cone as shown. If a point charge +q is kept at the vertex of thecone, the electric flux that comes out of the base of the cone is
 Aq4ε0Bq(2−√3)4ε0CzeroDq2ε0
Aq4ε0Bq(2−√3)4ε0CzeroDq2ε0The position vector of four points A, B, C and D are a,b,c and d respectively . If a- b = 2(d-c) the
AAB and CD bisectsBBD and AC bisectsCAB and CD trisectsDBD and AC trisects
point charge q is placed on the top of a cone of semi vertex angle theta .The electric flux through the base of the cone is
View SolutionA uniform solid cone of height 40 cm is shown in figure. The distance of centre of mass of the cone from point B (centre of the base) is :
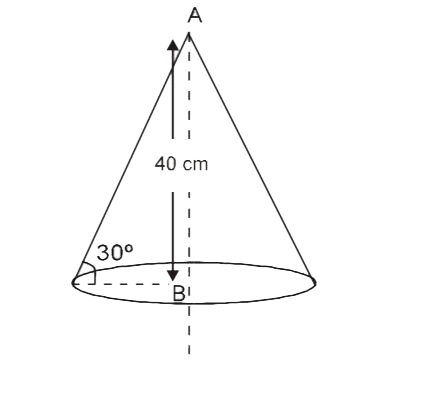
View SolutionA uniform solid cone of height 40 cm is shown in figure. The distance of centre of mass of the cone from point B (centre of the base) is :
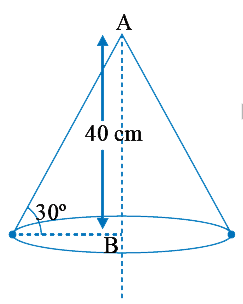
View SolutionThe number of surfaces of a cone has, is (a) 1 (b) 2 (c) 3 (d) 4
View SolutionThe position vector of four points A, B, C and D are a,b,c and d respectively . If a- b = 2(d-c) the
View Solution