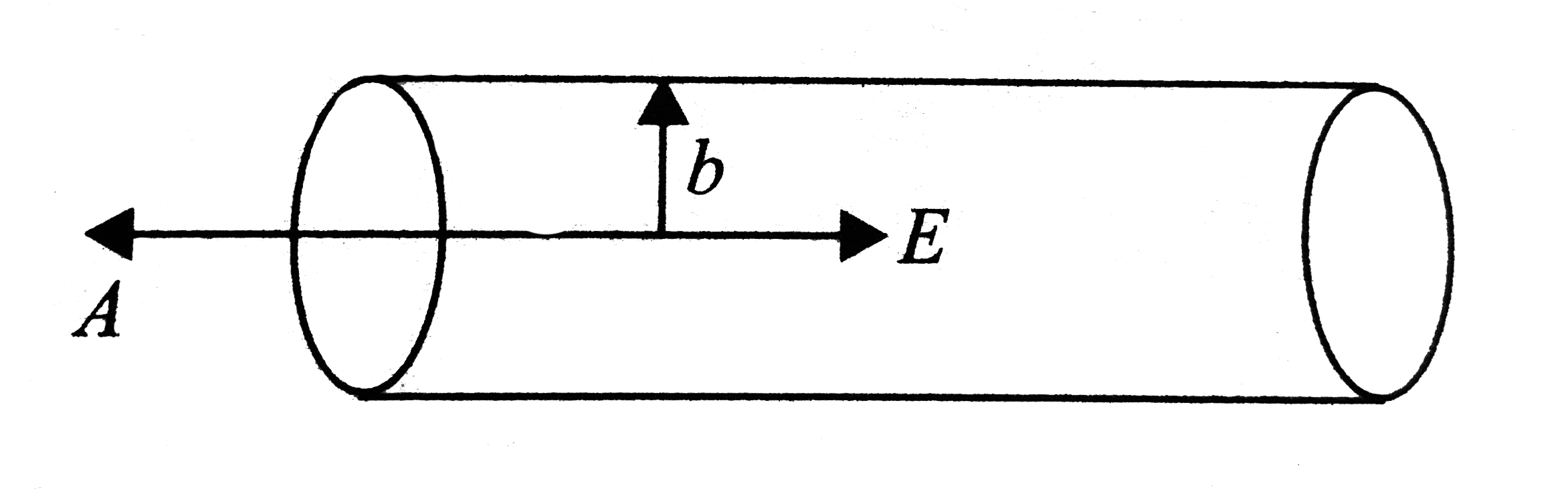
A cylinder of length L and radius b has its axis coincident with x-axis. The electric field in this region is →E=200ˆi. Find the flux through the left end of the cylinder.
0
200πb2
100πb2
−200πb2
The correct Answer is:D
d. ϕ=EAcosθ=Eπb2cos180∘=−200πb2
Topper's Solved these Questions
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICSChapter:ELECTRIC FLUX AND GAUSS LAWExercise:Multiple Correct
Explore 8 Videos
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICSChapter:ELECTRIC FLUX AND GAUSS LAWExercise:Comprehension
Explore 36 Videos
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICSChapter:ELECTRIC FLUX AND GAUSS LAWExercise:Subjective
Explore 12 Videos
- ELECTRIC CURRENT AND CIRCUITBook:CENGAGE PHYSICSChapter:ELECTRIC CURRENT AND CIRCUITExercise:Interger
Explore 8 Videos
- ELECTRIC POTENTIALBook:CENGAGE PHYSICSChapter:ELECTRIC POTENTIALExercise:DPP 3.5
Explore 14 Videos
Similar Questions
A cylinder of length L and radius b has its axis coincident with x-axis. The electric field in this region is →E=200ˆi. Find the flux through the left end of the cylinder.
View SolutionA thin straight infinitely long conducting wire having charge density λ is enclosed by a cylinder surface of radius r and length l, its axis coinciding with the length of the wire. Find the expression for the electric flux through the surface of the cylinder.
View Solution
Knowledge Check
A cylinder of length L and radius b has its axis coincident with the x-axis. The electric field in the region →E=200ˆi. Find the flux through (i) the left end of cylinder (ii) the right end of cylinder (iii) the cylinder curved surface, (iv) the closed surface area of the cylinder .
A(i) −100πb2(ii)100πb2(iii)50πb2(iv)50πb2B(i)−200πb2(ii)200πb2(iii)0(iv)0C(i)−100πb2(ii)100πb2(iii)100πb2(iv)100πb2D(i)−200πb2(ii)200πb2(iii)200πb2(iv)200πb2A hollow cylinder of length L and radius R having surface area A is placed horizontally with its axis parallel to an external field E. The electric flux through the surface of the cylinder is
AZeroB2πRLEC2πR2EDE . AA hollow cylinder of length L and radius R having surface area A is placed horizontally with its axis parallel to an external field E. The electric flux through the surface of the cylinder is
AZeroB2πRLEC2πR2EDE . A
A thin straight infinitely long conducting wire having charge density λ enclosed bya cylindrical surface of radius r and length lr, its axis coinciding with the length of the wire. Find the expression for the electric flux through the surface of the cylinder.
View SolutionA uniform electric field →E=−ExˆiN/C for x<0 exists. A right circular cylinder of length lcm and radius rcm has its centre at the origin and its axis along X-axis. Find out the net outward flux. What is the net charge within the cyclinder ?
View SolutionA hollow half cylinder surface of radius R and length l is placed in a uniform electric field →E. Electric field is acting perpendicular on the plane ABCD. Find the flux through the curved surface of the hollow cylindrical surface

View SolutionA cylinder of 500 g and radius 10 cm has moment of inertia (about its natural axis)
View SolutionA cylinder of length L has a charge of magnitude q. The electric intensity at a point at a distance r from the axis of the cylinder is
View Solution

