A cylinder of length L has a charge of magnitude q. The electric intensity at a point at a distance r from the axis of the cylinder is
E=14π∈0K⋅qr2
E=12π∈0k⋅qrL
E=σ/∈0k
none of these
The correct Answer is:B
Step by step video, text & image solution for A cylinder of length L has a charge of magnitude q. The electric intensity at a point at a distance r from the axis of the cylinder is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
An infinitely long solid cylinder of radius R with uniform volume charge density ρ has a spherical cavity of radius R2 with its centre on the axis of the cylinder as shown in the figure. The magnitude of the electric field at a point P which is at a distance 2R from the axis of the cylinder is given by 23ρR6Kε0. What is the value of K ?
View SolutionA dielectric cylinder of radius a is infinitely long. It is non-uniformly charged such that volume charge density ρ varies directly as the distance from the cylinder. Calculate the electric field intensity due to it at a point located at a distance r from the axis of the cylinder. Given that ρ is zero at the axis and it is equal to ρ on the surface of cylinder. Also calculate the potential difference between the axis and the surface. [ρr23∈0a,ρa29∈0]
View Solution
Knowledge Check
A sphere of radius R has a charge density σ. The electric intensity at a point at a distance r from its centre is
AE=σR2∈0kr2BE=σ∈0kCE=R2DE=∈0kr2σ2Consider a sphere of radius R and cylinder of length L. If both have same charge density σ and Es and Ee are electric intensity at a point at a distance r from axis of sphere and cylinder respectively, then Es=
AEcRrBEcrRCEcr2RDEcR2rConsider a sphere of radius R and cylinder of length L. If both have same charge density σ and EsandEc are electric intensity at a point at a distance r from axis of sphere and cylinder respectively, then Es equal to
AEcRrBEcrRC2EcrRDEcr2R
An infinitely long solid cylinder of radius R has a uniform volume charge density ρ. It has a spherical cavity of radius R2 with its center on the axis of the cylinder, as shown in the figure. The magnitude of the electric field at the point P, which at a distance 2 R (from the axis of the cylinder, is given by the expression 23ρR16nɛ0, The value of n is
'(##CEN_KSR_PHY_JEE_C18_E01_040_Q24##)'
View SolutionAn infinitely long solid cylinder of radius R has a uniform volume charge density ρ. It has a spherical cavity of radius R/2 with its centre on the axis of cylinder, as shown in the figure. The magnitude of the electric field at the point P, which is at a distance 2R form the axis of the cylinder, is given by the expression 23rR16ke0 . The value of k is .
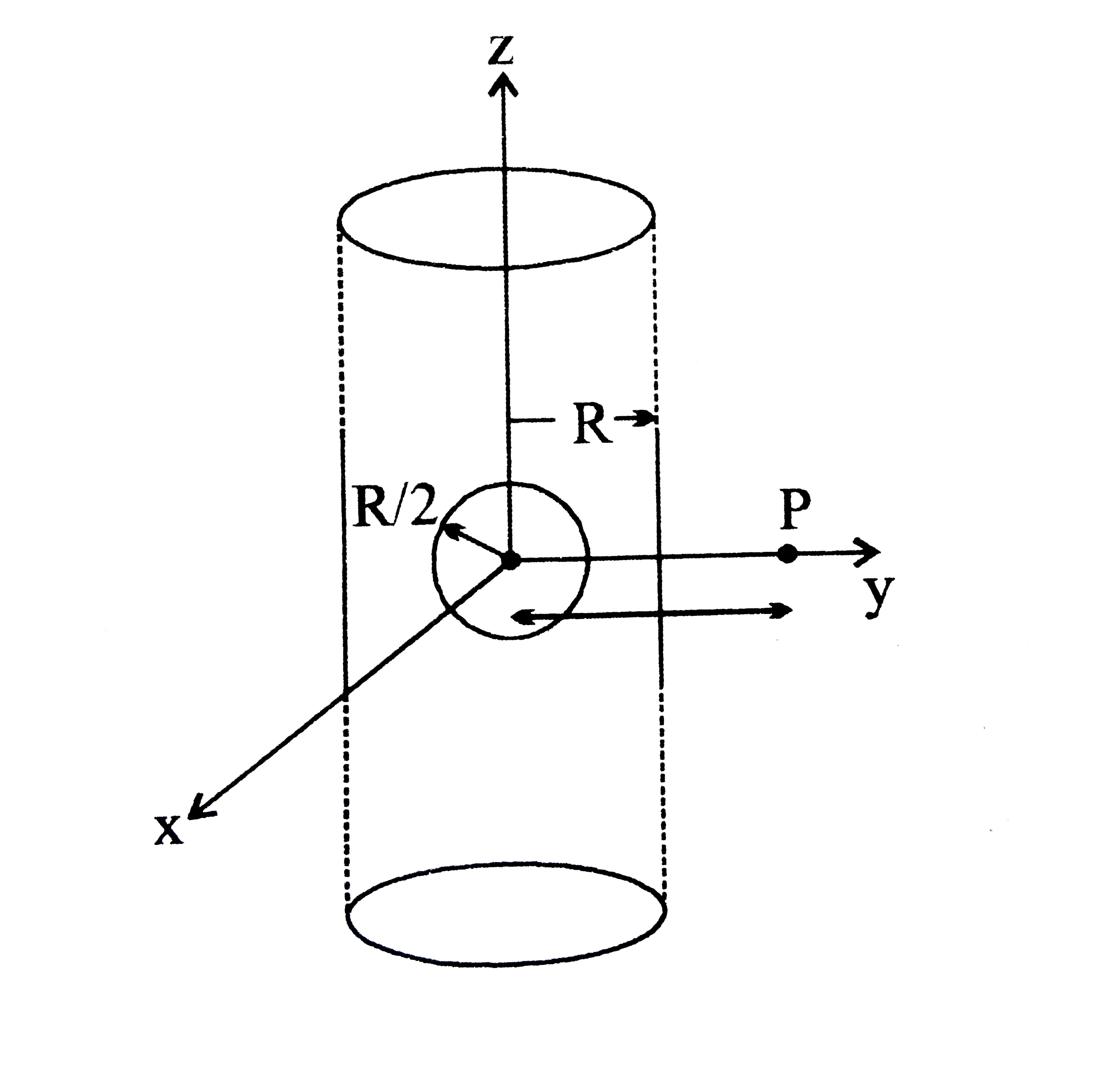 .
.
View SolutionAn infinitely long solid cylinder of radius R has a uniform volume charge density ρ. It has a spherical cavity of radius R/2 with its centre on the axis of cylinder, as shown in the figure. The magnitude of the electic field at the point P, which is at a distance 2R form the axis of the cylinder, is given by the expression 23rR16ke0 . The value of k is .
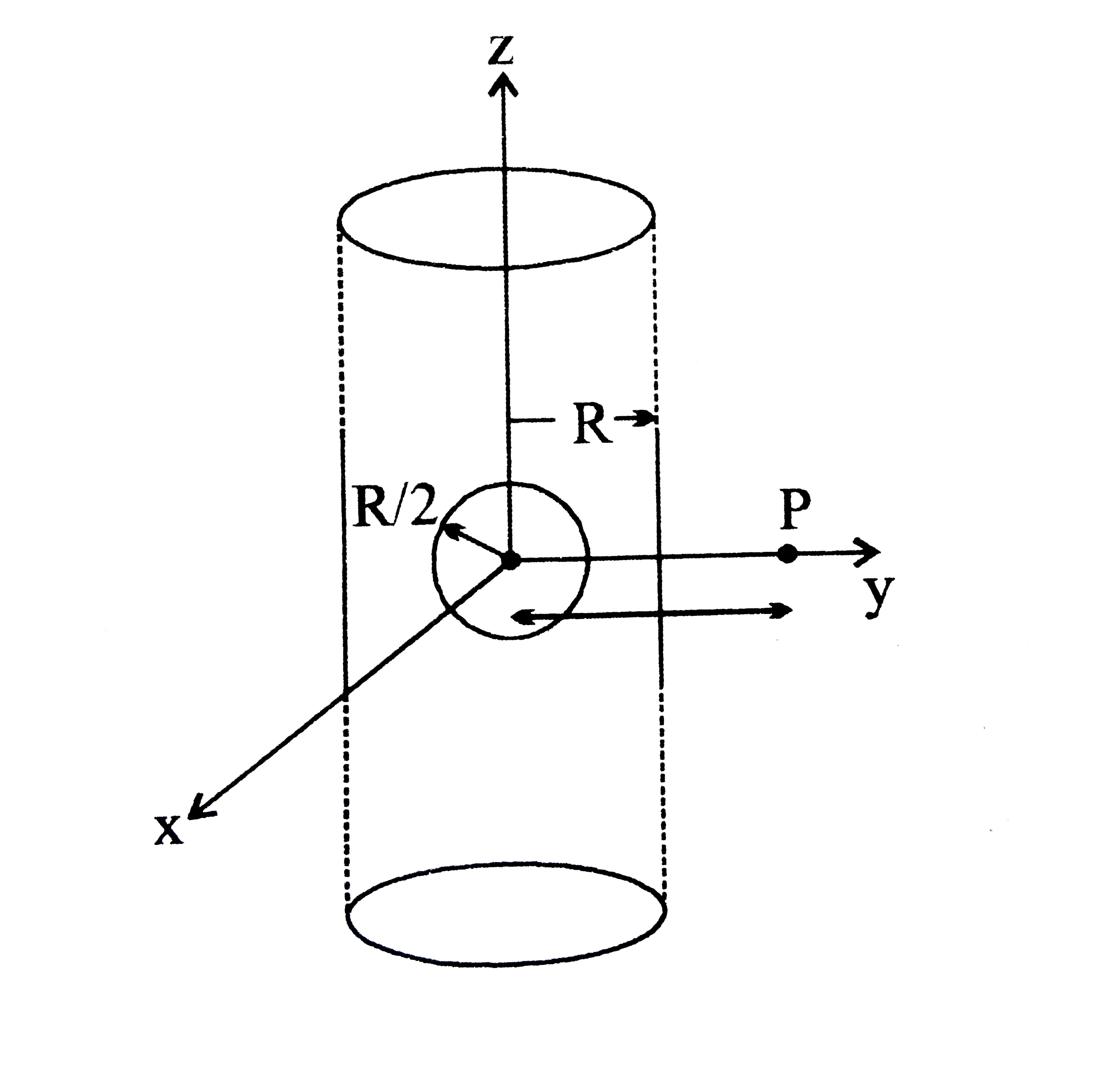 .
.
View Solution(a) There is a long uniformly charged cylinder having a volume charge density of ρC/m3. Radius of the cylinder is R. Find the electric field at a point at a distance x from the axis of the cylinder for following cases (i) x lt R (ii) x gt R What is the maximum field produced by the charge distribution at any point? (b) The cylinder described in (a) has a long cylindrical cavity. The axis of cylindrical cavity is at a distance a from the axis of the charged cylinder (see figure). Find electric field inside the cavity.
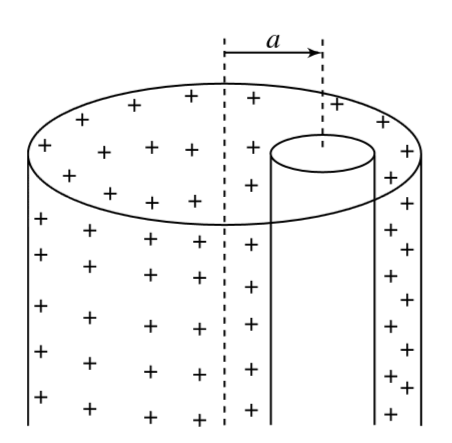
View SolutionIf σ is surface density of charge on the charged cylinder of radius R, then electric intensity E at outer point at a distance r from its axis is
View Solution

