If σ is surface density of charge on the charged cylinder of radius R, then electric intensity E at outer point at a distance r from its axis is
σR∈0kr
σr∈0kR
σ∈0k
σ2R∈0kr
The correct Answer is:A
Step by step video, text & image solution for If sigma is surface density of charge on the charged cylinder of radius R, then electric intensity E at outer point at a distance r from its axis is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
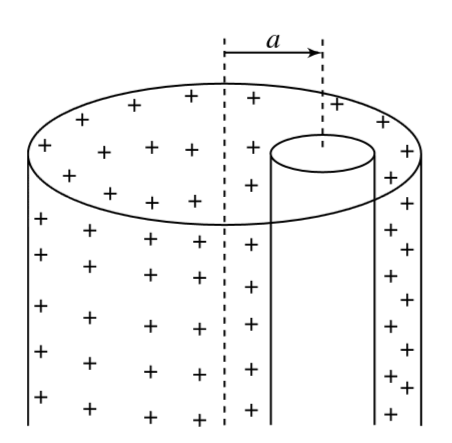
(a) There is a long uniformly charged cylinder having a volume charge density of ρC/m3. Radius of the cylinder is R. Find the electric field at a point at a distance x from the axis of the cylinder for following cases (i) x lt R (ii) x gt R What is the maximum field produced by the charge distribution at any point? (b) The cylinder described in (a) has a long cylindrical cavity. The axis of cylindrical cavity is at a distance a from the axis of the charged cylinder (see figure). Find electric field inside the cavity.
View Solution" Electric field intensity due to a point charge " "q" ' at a distance 'r' from it is "
View Solution
Knowledge Check
If charge q is induced on outer surface of sphere of radius R, then intensity at a point P at a distance S from its centre is
Ainversely proportional to (S+R)2Binversely proportional to R2Cinversely proportional to S2Ddirectly proportional to S2A sphere of radius R has a charge density σ. The electric intensity at a point at a distance r from its centre is
AE=σR2∈0kr2BE=σ∈0kCE=R2DE=∈0kr2σ2A cylinder of length L has a charge of magnitude q. The electric intensity at a point at a distance r from the axis of the cylinder is
AE=14π∈0K⋅qr2BE=12π∈0k⋅qrLCE=σ/∈0kDnone of these
A dielectric cylinder of radius a is infinitely long. It is non-uniformly charged such that volume charge density ρ varies directly as the distance from the cylinder. Calculate the electric field intensity due to it at a point located at a distance r from the axis of the cylinder. Given that ρ is zero at the axis and it is equal to ρ on the surface of cylinder. Also calculate the potential difference between the axis and the surface. [ρr23∈0a,ρa29∈0]
View SolutionIf charge q induced on outer surface of sphere of radius R, then intensity at point P at distance S from centre is
View SolutionIf σ is the surface charge density off a charge for a charged sphere of radius R. kept in a medium of dielectric constant K, then the electric intensity at a distance r from its centre where rgtR, is (ε0=permittivity of free space)
View SolutionA charged cylinder of radius 3 mm has surface density of charge 4μC/m2. It is placed in a medium of dielectric constant 6.28. The electric intensity at a point at a distance of 1.5 M from its axis is
View SolutionThe electric field at a distance r from a long wire having charge per unit length λ is
View Solution

