A dielectric cylinder of radius a is infinitely long. It is non-uniformly charged such that volume charge density ρ varies directly as the distance from the cylinder. Calculate the electric field intensity due to it at a point located at a distance r from the axis of the cylinder. Given that ρ is zero at the axis and it is equal to ρ on the surface of cylinder. Also calculate the potential difference between the axis and the surface. [ρr23∈0a,ρa29∈0]
Step by step video & image solution for A dielectric cylinder of radius a is infinitely long. It is non-uniformly charged such that volume charge density rho varies directly as the distance from the cylinder. Calculate the electric field intensity due to it at a point located at a distance r from the axis of the cylinder. Given that rho is zero at the axis and it is equal to rho on the surface of cylinder. Also calculate the potential difference between the axis and the surface. [(rhor^(2))/(3in_(0)a),(rhoa^(2))/(9in_(0))] by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTROSTATICSBook:PHYSICS GALAXY - ASHISH ARORAChapter:ELECTROSTATICSExercise:Partice Exercise 1.2
Explore 1 Video
- ELECTROSTATICSBook:PHYSICS GALAXY - ASHISH ARORAChapter:ELECTROSTATICSExercise:Partice Exercise 1.3
Explore 1 Video
- ELECTROSTATICSBook:PHYSICS GALAXY - ASHISH ARORAChapter:ELECTROSTATICSExercise:Partice Exercise 1.1
Explore 1 Video
- ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTBook:PHYSICS GALAXY - ASHISH ARORAChapter:ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTExercise:Advance MCQs
Explore 33 Videos
- GEOMETRICAL OPTICSBook:PHYSICS GALAXY - ASHISH ARORAChapter:GEOMETRICAL OPTICSExercise:Unsolved Numerical Problems
Explore 107 Videos
Similar Questions
A solid cylinder carries current of 1 A uniformly distributed over its cross sectional area. Calculate the magnetic field induction at point P, at a distance of 3 cm from the axis of cylinder, if its radius is 7 cm .
View SolutionA ball of radius R is uniformly charged with the volume density ρ. Find the flux if the electric field strength vector across the balls section formed by the plane located at a distance r0<R from the centre of the ball.
View Solution
Knowledge Check
A cylinder of length L has a charge of magnitude q. The electric intensity at a point at a distance r from the axis of the cylinder is
AE=14π∈0K⋅qr2BE=12π∈0k⋅qrLCE=σ/∈0kDnone of theseIf σ is surface density of charge on the charged cylinder of radius R, then electric intensity E at outer point at a distance r from its axis is
AσR∈0krBσr∈0kRCσ∈0kDσ2R∈0krHow does the electric field (E) between the plates of a charged cylindrical capacitor vary with the distance r from the axis of the cylinder ?
AE∝1r2BE∝1rCE∝r2DE∝r
A solid non-conduction cylinder of radius R is charge such that volume charge density is proporation to r where r is distance from axis. The electric field E at a distance r(r<R) well depend on r as.
View SolutionAn infinitely long solid cylinder of radius R with uniform volume charge density ρ has a spherical cavity of radius R2 with its centre on the axis of the cylinder as shown in the figure. The magnitude of the electric field at a point P which is at a distance 2R from the axis of the cylinder is given by 23ρR6Kε0. What is the value of K ?
View SolutionThere is one long non-conducting solid cylinder of radius R. The volume charge density is given by ρ=kx2 where k is a constant and x is the distance of the point from centre of cylinder. Electric field intensity inside the cylinder at a distance x from the centre is
View SolutionInside a uniformly charged infinitely long cylinder of radius 'R' and volume charge density 'rho' there is a spherical cavity of radius 'R//2'. A point 'P' is located at a dsintance 2R from the axis of the cylinder as shown. Then the electric field strength at the point 'P' is
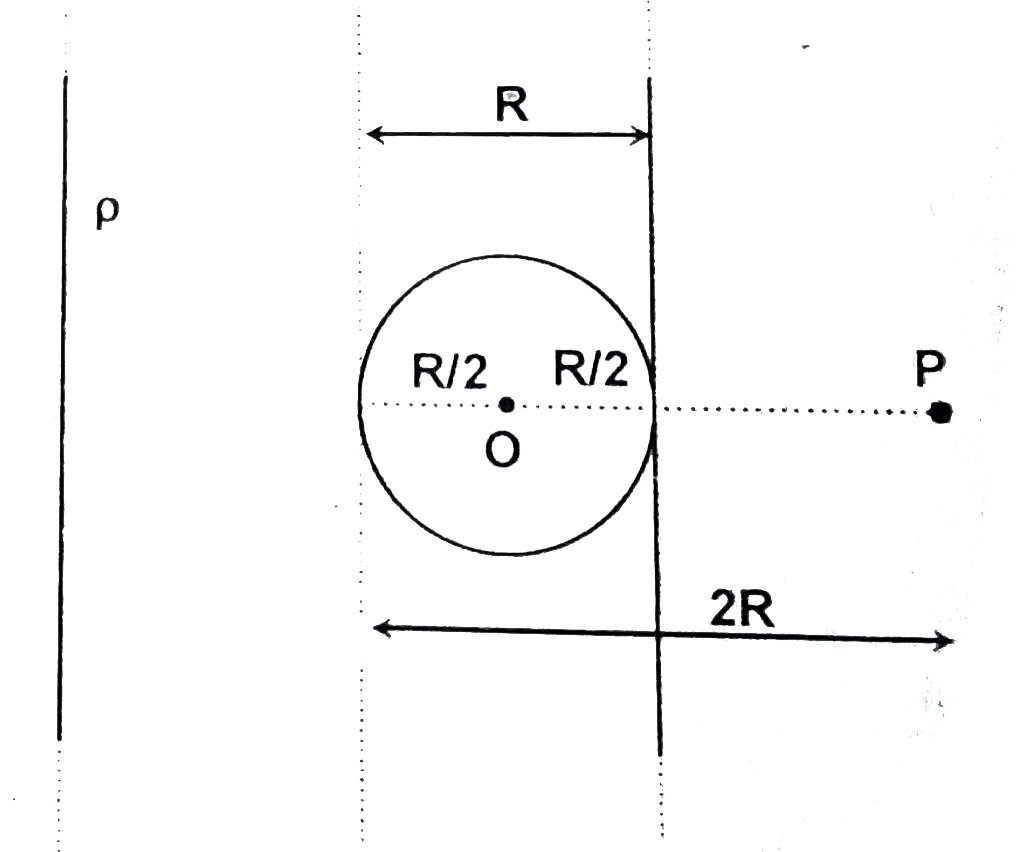
View SolutionThe electric intensity due to a charged conducting cylinder of radius 0.1 m at a distance of 1 m from the axis of the cylinder of charge density 1.77μC/m in a dielectric medium of dielectric constant 2 is
View Solution

