Electric field at a point of distance r from a uniformly charged wire of infinite length having linear charge density λ is directly proportional to
r−1
r
r2
r−2
The correct Answer is:A
To solve the question regarding the electric field at a distance r from a uniformly charged wire of infinite length with linear charge density λ, we will derive the formula step by step.
1. Understand the Configuration:
We have an infinite straight wire with a uniform linear charge density λ. The goal is to find the electric field E at a distance r from the wire.
Hint: Visualize the wire and the point where you want to calculate the electric field.
2. Use Gauss's Law:
We will apply Gauss's Law, which states that the electric flux through a closed surface is equal to the charge enclosed divided by the permittivity of free space ϵ0.
ΦE=Qencϵ0
Hint: Remember that the total charge enclosed is related to the linear charge density and the length of the wire.
3. Choose a Gaussian Surface:
For an infinite wire, the most suitable Gaussian surface is a cylindrical surface coaxial with the wire. Let the length of the cylinder be L and its radius be r.
Hint: The symmetry of the problem allows us to assume that the electric field E is constant over the curved surface of the cylinder.
4. Calculate the Charge Enclosed:
The charge enclosed by the Gaussian surface is given by:
Qenc=λL
Hint: Linear charge density λ is charge per unit length.
5. Calculate the Electric Flux:
The electric flux through the curved surface of the cylinder is:
ΦE=E⋅A=E⋅(2πrL)
where A is the surface area of the cylindrical surface.
Hint: The electric field is perpendicular to the surface area vector on the curved surface.
6. Apply Gauss's Law:
Set the electric flux equal to the charge enclosed divided by ϵ0:
E⋅(2πrL)=λLϵ0
Hint: Notice that L cancels out from both sides.
7. Solve for Electric Field E:
Rearranging the equation gives:
E=λ2πϵ0r
Hint: This shows how E depends on r.
8. Relate to Proportionality:
The formula can be rewritten as:
E∝λr
This indicates that the electric field E is inversely proportional to the distance r from the wire.
Hint: In terms of proportionality, you can express this as E∝r−1.
Conclusion
Thus, the electric field at a point at a distance r from a uniformly charged wire of infinite length having linear charge density λ is directly proportional to λr or inversely proportional to r.
Final Answer
The electric field E is inversely proportional to the distance r from the wire.
We have an infinite straight wire with a uniform linear charge density λ. The goal is to find the electric field E at a distance r from the wire.
We will apply Gauss's Law, which states that the electric flux through a closed surface is equal to the charge enclosed divided by the permittivity of free space ϵ0.
For an infinite wire, the most suitable Gaussian surface is a cylindrical surface coaxial with the wire. Let the length of the cylinder be L and its radius be r.
The charge enclosed by the Gaussian surface is given by:
Qenc=λL
The electric flux through the curved surface of the cylinder is:
ΦE=E⋅A=E⋅(2πrL)
where A is the surface area of the cylindrical surface.
Set the electric flux equal to the charge enclosed divided by ϵ0:
E⋅(2πrL)=λLϵ0
Rearranging the equation gives:
E=λ2πϵ0r
The formula can be rewritten as:
E∝λr
This indicates that the electric field E is inversely proportional to the distance r from the wire.
Thus, the electric field at a point at a distance r from a uniformly charged wire of infinite length having linear charge density λ is directly proportional to λr or inversely proportional to r.
The electric field E is inversely proportional to the distance r from the wire.
Topper's Solved these Questions
- ELECTROSTATICSBook:DC PANDEYChapter:ELECTROSTATICSExercise:Match the columns
Explore 5 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBook:DC PANDEYChapter:ELECTROSTATIC POTENTIAL AND CAPACITORSExercise:(C) Chapter exercises
Explore 50 Videos
- GRAVITATIONBook:DC PANDEYChapter:GRAVITATIONExercise:All Questions
Explore 120 Videos
Similar Questions
Find the electric field at the centre of a uniformly charged semicircular ring of radius R. Linear charge density is λ
View SolutionWhat is the electric field intensity at any point on the axis of a charged rod of length 'L' and linear charge density λ? The point is separated from the nearer end by a.
View Solution
Knowledge Check
The electric field at a distance r from a long wire having charge per unit length λ is
Ak(λr2)Bk(λr)Ck(λ2r)Dk(2λr)Let E1(r), E2(r) and E3(r) be the respectively electric field at a distance r from a point charge Q, an infinitely long wire with constant linear charge density λ, and an infinite plane with uniform surface charge density σ. If E1(r0)=E2(r0)=E3(r0) at a given distance r0, then
A(a) Q=4σπr20B(b) r0=λ2πσC(c) E1(r0/2)=2E2(r0/2)D(d) E2(r0/2)=4E3(r0/2)A charge particle q is released at a distance R∘ from the infinite long wire of linear charge density λ. Then velocity will be proportional to (At distance R from the wire)
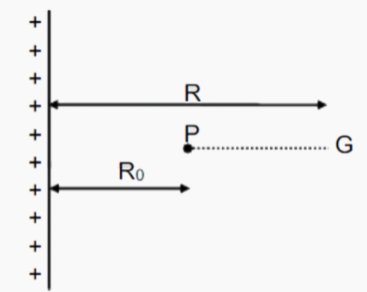 AR3BeR/R0CR2D[n(RR0)]−1/2
AR3BeR/R0CR2D[n(RR0)]−1/2
Calculate electric field at a point on axis, which at a distance x from centre of uniformly charged disc having surface charge density σ and R which also contains a concentric hole of radius r.
View SolutionElectric field at a point near a uniformaly charged infinite plane sheet having surface density of charge σ is given as E= ________________
View SolutionAn electric dipole of moment p is kept at a distance r form an infinte long charged wire of linear charge density λ as shown.Find the force acting on the dipole?

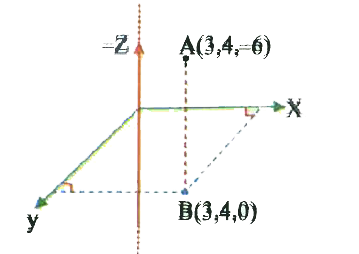
View SolutionFind electric field at point A, B, C, D due to infinitely long uniformly charged wire with linear charge density λ and kept along z-axis (as shown in figure). Assume that all the parameters are in S.l. units.

View SolutionFind ratio of electric at point A and B. Infinitely long uniformly charged wire with linear charge density λ is kept along z-axis:
View Solution

