In the arrangement shown in figure, pulley and string are light. Friction coefficient between the two blocks is μ whereas the incline is smooth. Block A has mass m and difference in mass of the two blocks isδm. Find minimum value of m for which the system will not accelerate when released from rest.
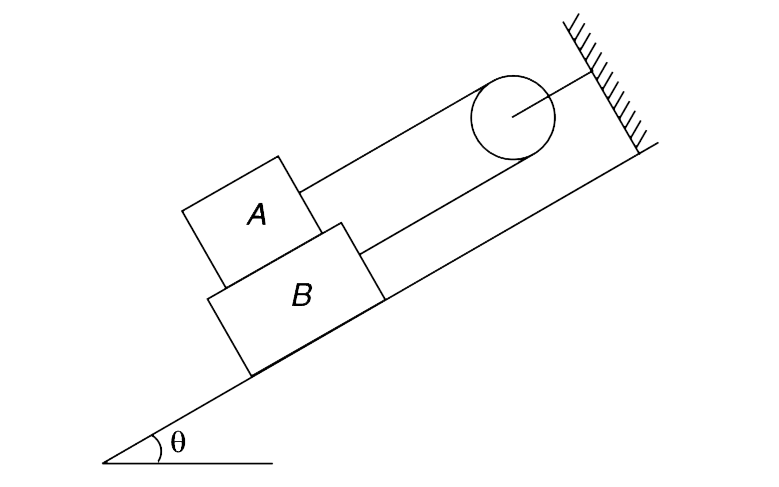
The correct Answer is:μmin=δm2mtanθ
Step by step video, text & image solution for In the arrangement shown in figure, pulley and string are light. Friction coefficient between the two blocks is mu whereas the incline is smooth. Block A has mass m and difference in mass of the two blocks isdeltam. Find minimum value of m for which the system will not accelerate when released from rest. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In the arrangement shown in figure pulley P can move whereas other two pulleys are fixed. All of them are light. String is light and inextensible. The coefficient of friction between 2 kg and 3 kg block is μ=0.75 and that between 3 kg block and the table is μ=0.5. The system is released from rest
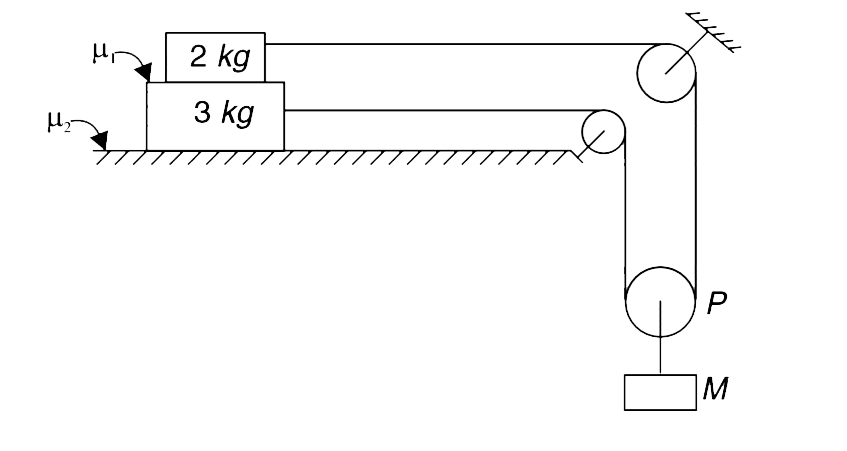
(i) Find maximum value of mass M, so that the system does not move. Find friction force between 2 kg and 3 kg blocks in this case.
(ii) If M = 4 kg, find the tension in the string attached to 2 kg block.
(iii) If M = 4 kg and μ1=0.9, find friction force between the two blocks, and acceleration of M.
(iv) Find acceleration of M if m1=0.75,m2=−0.9 and M = 4 kg.
View SolutionFind the acceleration of the block of mass M in the situation of figure. The coefficient of friction between the two blocks is μ1 and that between the bigger block and the ground is μ2.
View Solution
Knowledge Check
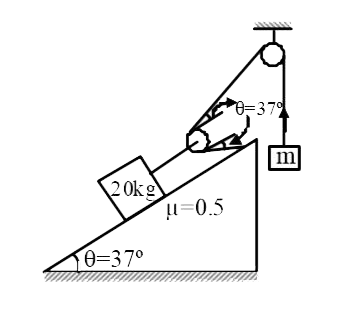
In the arrangement shown in figure, there is a friction force between the blocks of masses m and 2m. The mass of the suspended block is m. The block of mass m is stationary with respect to block of mass 2m. The minimum value of coefficient of friction between m and 2m is
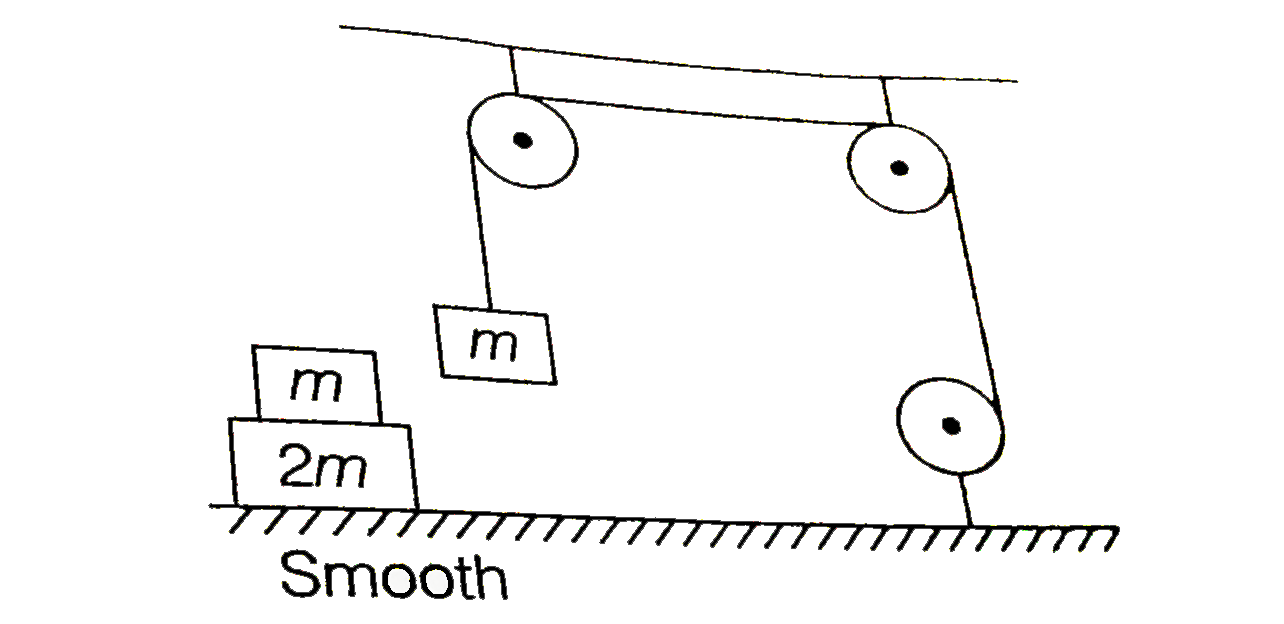 A12B1√2C14D13
A12B1√2C14D13For the arrangement shown in the figure the coefficient of friction between the two blocks is μ. If both the blocks are identical and moving ,then the acceleration of each block is
 AF2m−2μgBF2mCF2m−μgDzero
AF2m−2μgBF2mCF2m−μgDzeroAn arrangement of the masses and pulleys is shown in the figure. Strings connecting masses A and B with pulley are horizontal and all pulleys and strings are light. Friction coefficient between the surface and the block B is 0.2 and between block A and B is 0.7. The system is released from rest. (use g=10m/s2)
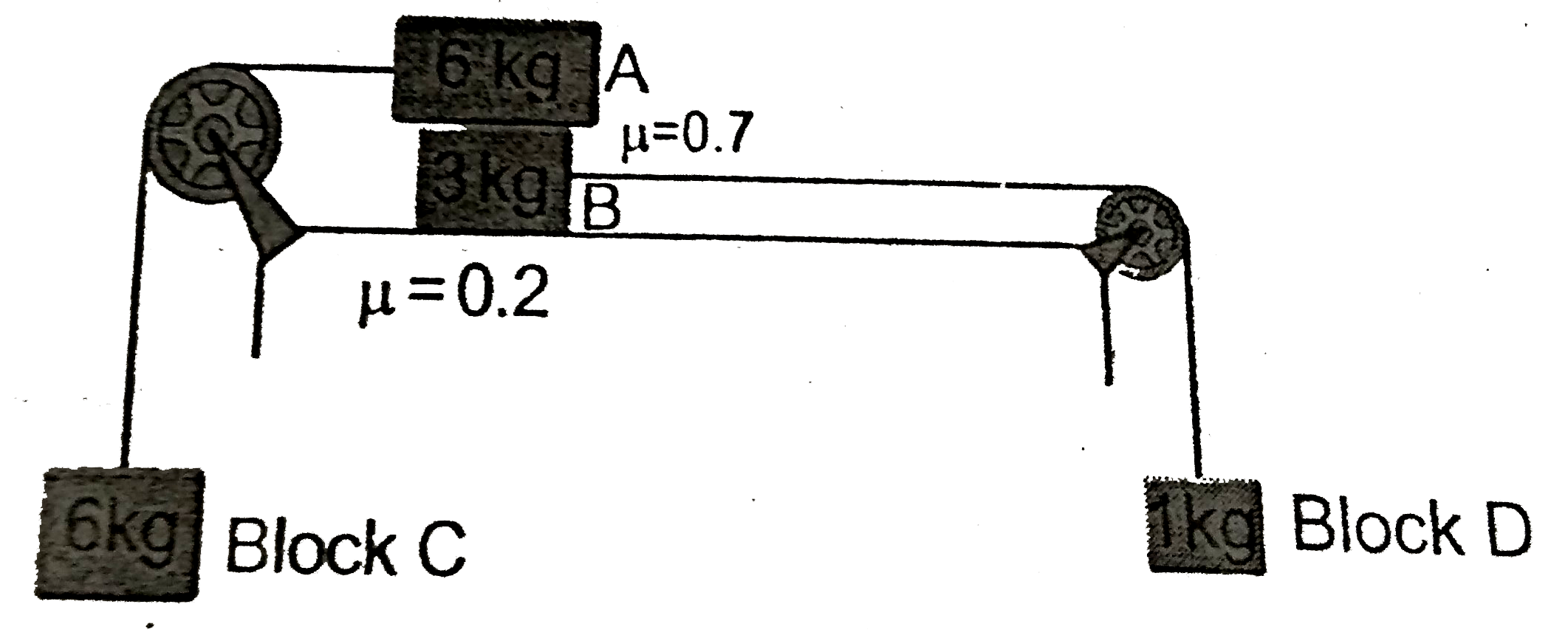 AThe magnitude of acceleration of the system is 2m/s2 and there is no slipping between block A and block B.BThe magnitude of friction force between block A and blockB is 42NCAcceleration of block C is 1m/s2 downwards.DTension in the string connecting block B and block D is 12N.
AThe magnitude of acceleration of the system is 2m/s2 and there is no slipping between block A and block B.BThe magnitude of friction force between block A and blockB is 42NCAcceleration of block C is 1m/s2 downwards.DTension in the string connecting block B and block D is 12N.
As shown in figure pulley is ideal and strings are massless.If mass m of hanging block is the minimum mass to set the equilibrium of system, then -
View SolutionThe coefficient of static friction between the two blocks shown in figure is μ and the table is smooth. What maximum horizontal forced F can be applied to he block of mass M so that the block move together?

View SolutionIn the arrangement shown in the figure, mass of the block B and A is 2m and m respectively. Surface between B and floor is smooth. The block B is connected to the block C by means of a string-pulley system. If the whole system is released, then find the minimum value of mass of block C so that A remains stationary w.e.t. B. Coefficient of friction between A and B is μ.

View Solution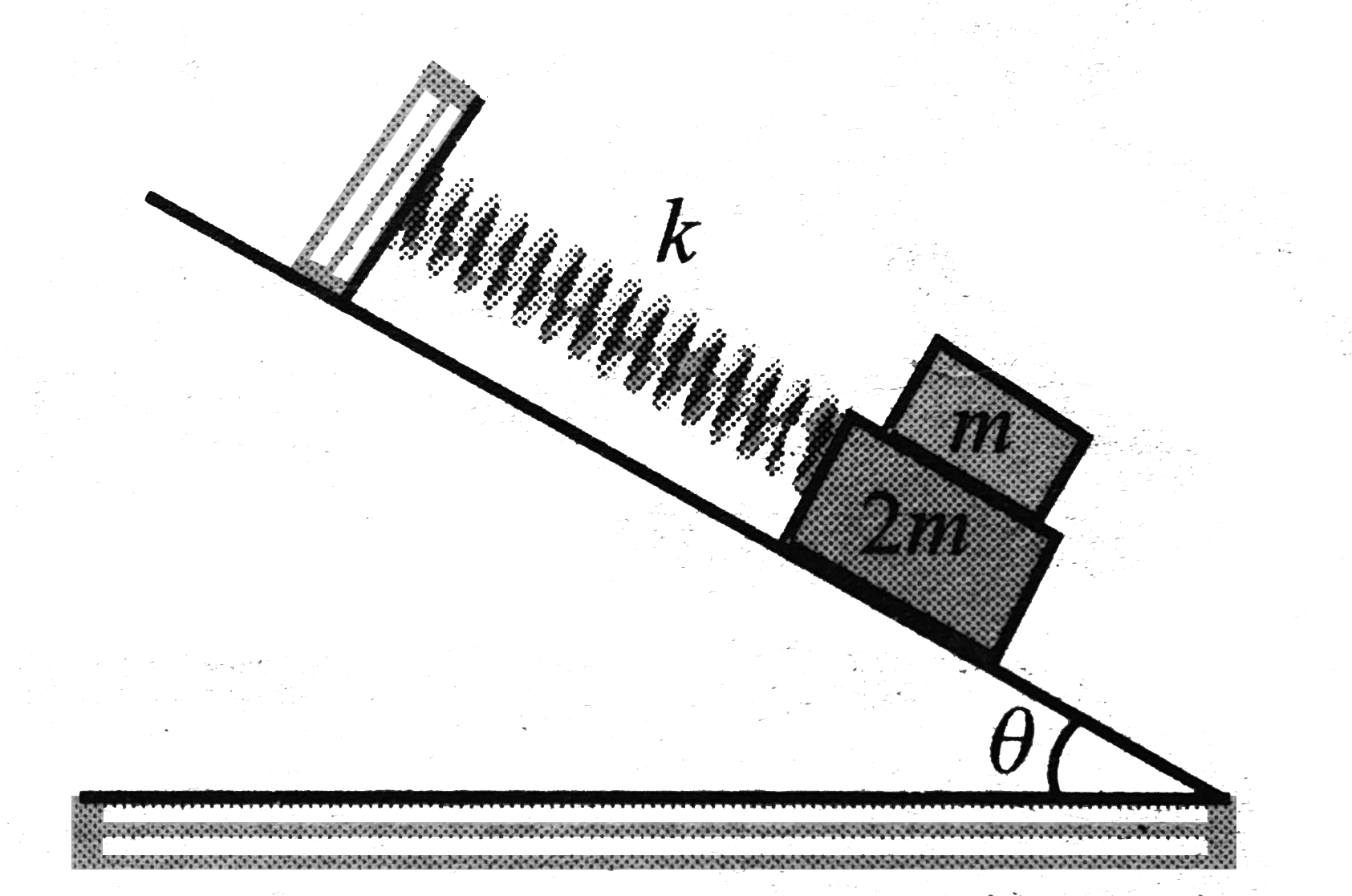
The coefficient of friction between block of mass m and 2m is μ=2tanθ. There is no friction between block of mass 2 m and inclined plane. The maximum amplitude of the two block system for which there is no relative motion between both the blocks is
View SolutionIn the arrangement shown in the figure mass of the block B and A are 2m , 8m respectively. Surface between B floor is smooth. The block B is connected to block C by means of a pulley. If the whole system is released then the minimum value of mass of the block C so that the block A remains stationary with respect to B is: (Coefficient of friction between A and B is μ and pulley is ideal).

View Solution
