A light rod AB is fitted with a small sleeve of mass m which can slide smoothly over it. The sleeve is connected to the two ends of the rod using two springs of force constant 2k and k (see fig). The ends of the springs at A and B are fixed and the other ends (connected to sleeve) can move along with the sleeve. The natural length of spring connected to A is l0. Now the rod is rotated with angular velocity w about an axis passing through end A that is perpendicular to the rod. Take kmω2=η and express the change in length of each spring (in equilibrium position of the sleeve relative to the rod) in terms of l0 and η.

The correct Answer is:x=l03η−1
Step by step video, text & image solution for A light rod AB is fitted with a small sleeve of mass m which can slide smoothly over it. The sleeve is connected to the two ends of the rod using two springs of force constant 2k and k (see fig). The ends of the springs at A and B are fixed and the other ends (connected to sleeve) can move along with the sleeve. The natural length of spring connected to A is l_(0). Now the rod is rotated with angular velocity w about an axis passing through end A that is perpendicular to the rod. Take (k)/(momega^(2)) = eta and express the change in length of each spring (in equilibrium position of the sleeve relative to the rod) in terms of l_(0) and eta. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A small sleeve of mass m=1/10kg can move along the diameter of a horizontal disc, which slides without friction along a guide rode. The sleeve is tied to the end of the rod with the aid of a massless spring whose force constant k=10N/m. When the spring is not under tension, the sleeve is at the oscillations of the sleeve when the disc rotates about its axis at the angular speed ω equal to a) 6 rad/s, b) 15 rad/s.

View SolutionTwo spring of force constants K and 2K are connected a mass m below The frequency of oscillation the mass is

View Solution
Knowledge Check
A particle of mass m is fixed to one end of a light spring of force constant k and unstretched length l. The other end of the spring is fixed on a vertical axis which is rotaing with an angular velocity ω. The increase in length of th espring will be
 Amω2lkBmω2lk−mω2Cmω2lk+mω2DNone of these
Amω2lkBmω2lk−mω2Cmω2lk+mω2DNone of theseA particles of mass m is fixed to one end of a light spring of force constant k and unstreatched length l. the system is rotated about the other end of the spring with an angular velocity ω in gravity free space. The increase in length of the spring is
 Amω2lkBmω2lk−mω2Cmω2lk+mω2Dnone of these
Amω2lkBmω2lk−mω2Cmω2lk+mω2Dnone of theseTwo blocks are connected to the two free ends of a spring of spring constant K . Both the blocks are moved apart to extend the psring beyond its natural length and then released . In subsequent motion
AAccelerations of both the objects are equal and opposite of each other .BVelocities of both the bjects are equal and opposite of each other .CForces acting on both the objects are equal and opposite of each otherDLinear momenta of both the objects are equal and opposite of each other .
A ring of mass m can slide over a smooth vertical rod. The ring is connected to a spring of force constant K=4mgR where 2R is the natural length of the spring. The other end spring is fixed to the ground at a horizontal distance 2R from the base of the rod. the mass is released at a height of 1.5 R from ground.
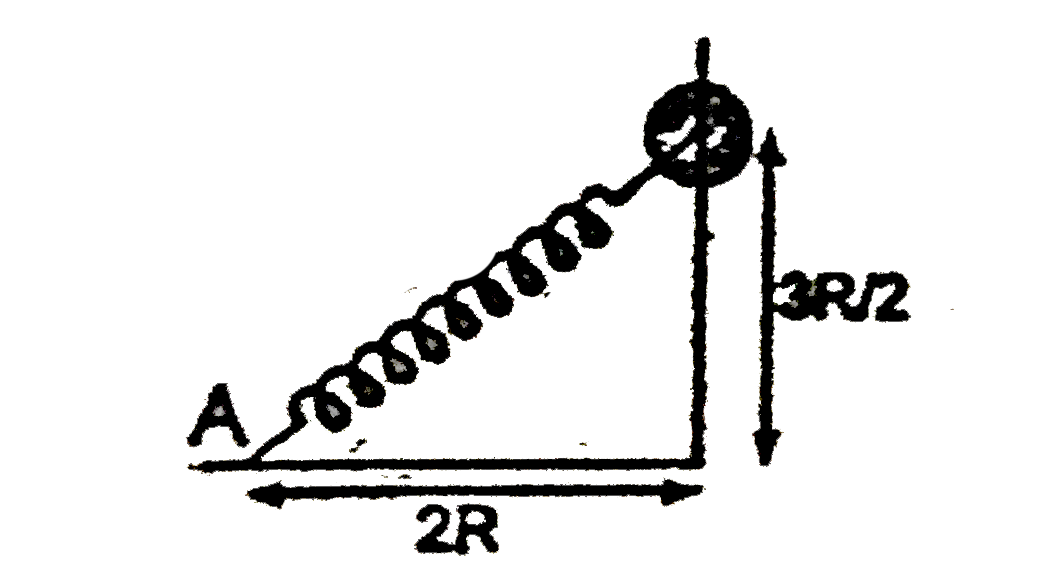
View SolutionTwo springs have force constants kA and kB such that kB=2kA. The four ends of the springs are stretched by the same force. If energy stored in spring A is E, then energy stored in spring B is.
View SolutionA block of mass m is connected at one end of spring fixed at other end having natural length l0 and spring constant K. The block is rotated with constant angular speed (ω) in gravity free space. Find the elongation in spring.
View SolutionA particle of mass m is fixed to one end of a massless spring of spring constant k and natural length l0. The system is rotated about the other end of the spring with an angular velocity ω ub gravity-free space. The final length of spring is
View SolutionTwo springs have force constants kA and kB such that kB=2kA. The four ends of the springs are stretched by the same force. If energy stored in spring A is E, then energy stored in spring B is.
View Solution