When force F applied on m2 and there is no friction between m1 and surface and the coefficient of friction between m1andm2 is μ… What should be the minimum value of F so that there is no relative motion between m1andm2
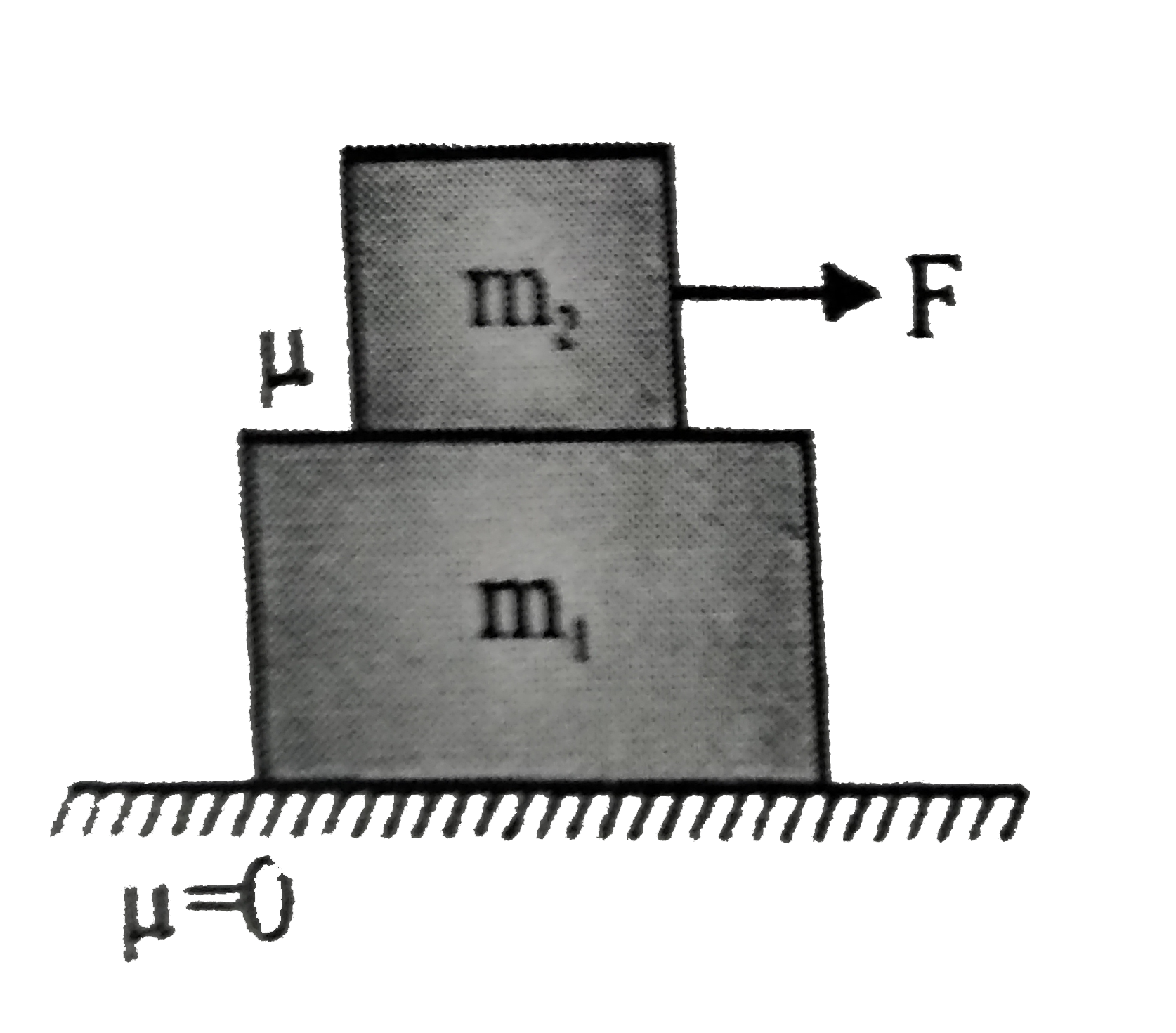
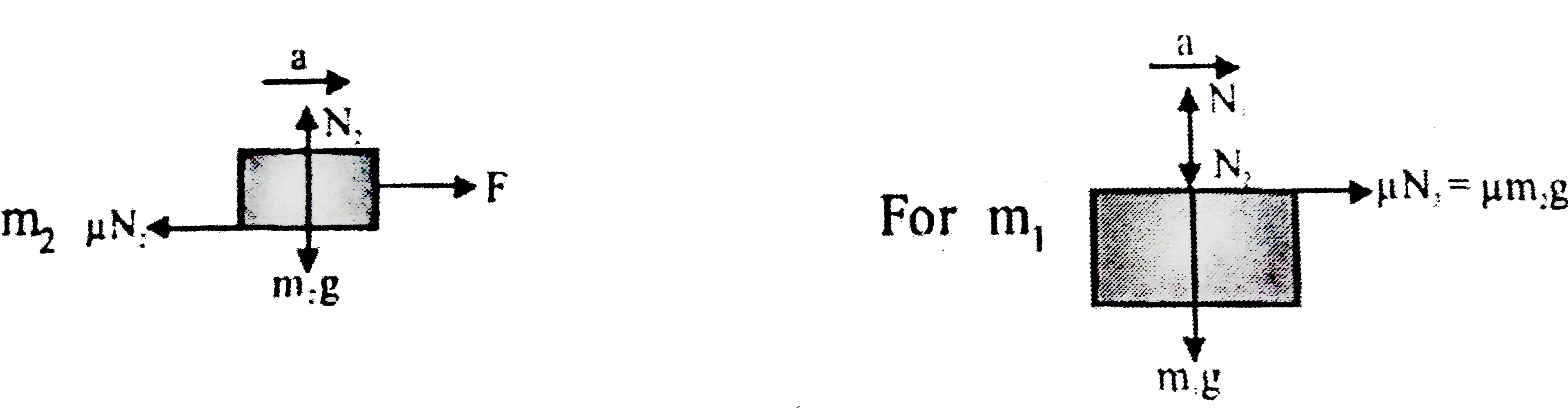
for system : acceleration =Fm1+m2
for m1:μm2g=m1a=m1(Fm1m2),Fmin=(m1+m2)(μ2gm1)
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (S-1)
26 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (S-2)
9 Videos
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - SOLVED EXAMPLE
28 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
Similar Questions
When force F applied on m1 and there is no friction between m1 and surface and the coefficient of friction between m1andm2 is μ. What should be the minimum value of F so that there is on relative motion between m1andm2

View SolutionWhen force F applied on m1 and surface. Is μ1 and the coefficient of friction between m1andm2 is μ2. What should be the minimum value of F so that there is no relative motion between m1andm2.

View Solution
Knowledge Check
In Fig. 7.150 , coefficient of friction between m2 and the horizontal surface is μ , minimum value of m so that the system has zero acceleration , is :
 Aμ(m1+m2)Bμ(m1+m2)Cm2−m1μDm1μ−m2
Aμ(m1+m2)Bμ(m1+m2)Cm2−m1μDm1μ−m2In the pulley arrangement shown in Fig the pulley p2 is movable .Assuming the coefficient of friction between m and surface to be μ the minimum value of M for which m is at rest is
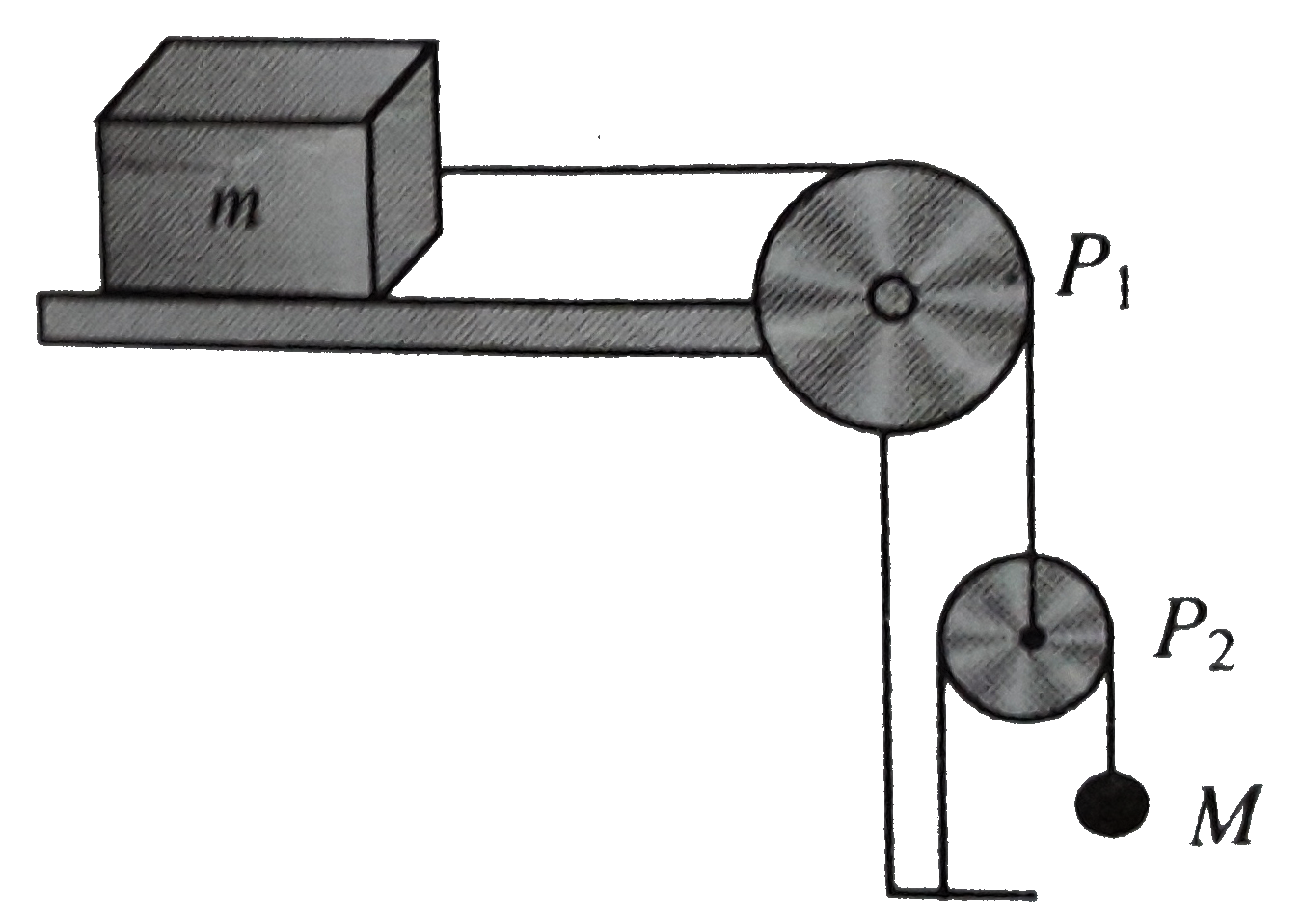 AM=μm2Bm=μM2CM=m2μDm=M2μ
AM=μm2Bm=μM2CM=m2μDm=M2μThe block each of mass 1kg are placed as shown .They are connected by a string which passes over a smooth (massless) pulley.

There is no friction between m1 and the ground.The coefficient of friction between m1 andm2 is 0.2A force F is applied to m2. Which of the fpllowing statement is/are correct?AThe system will be in equilibrium if F≤4NBF≥4N tension in the string will be 4NCF≥4N the frictional force between the blocks will be 2NDF=6N tension in the string will be 3N
The coefficient of friction between m2 and inclined plane is μ (shown in the figure). If m1m2=sinθ then
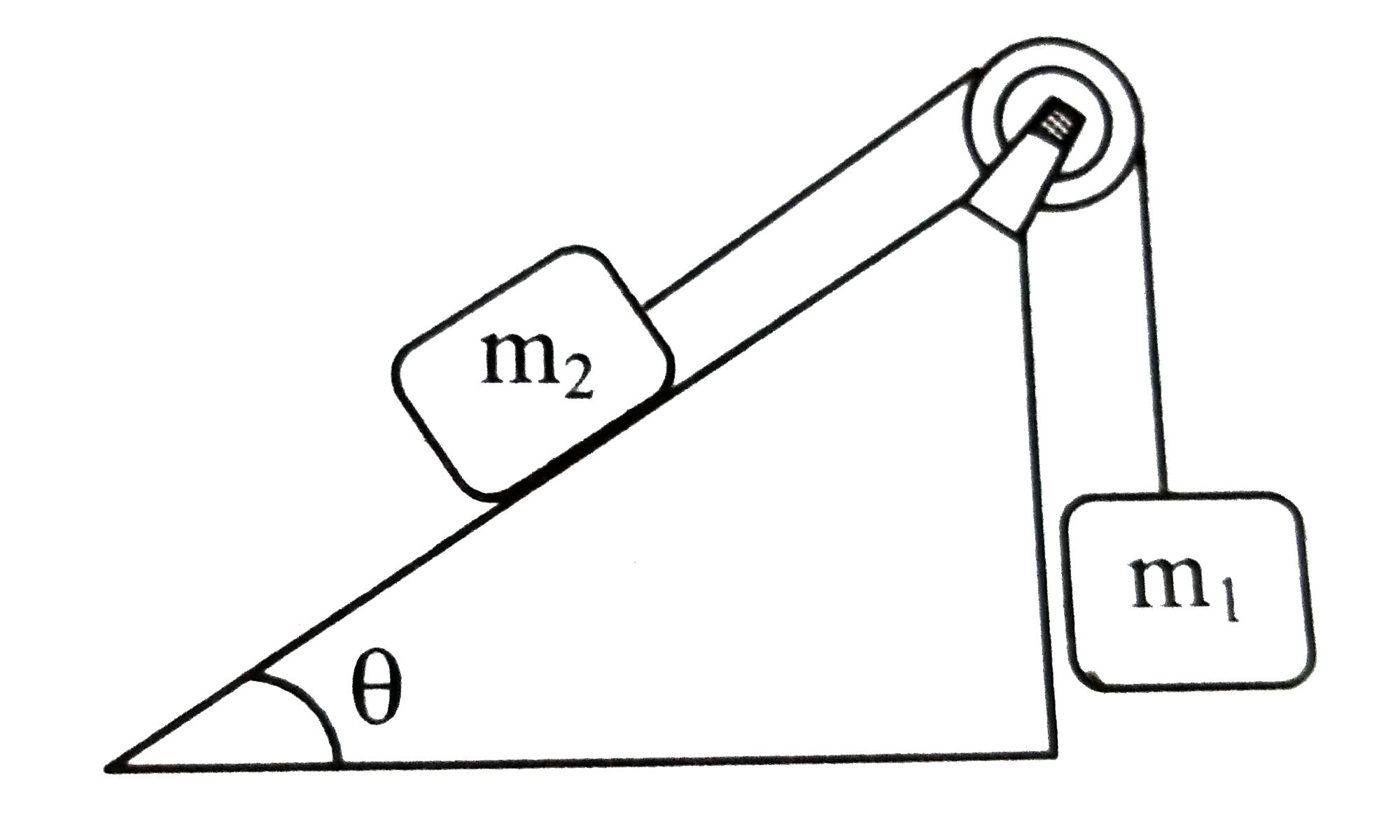
View SolutionThe arrangement shown in the figure, the systme of masses m1,m2 and m3 is being pushed by a force F applied on m1 horizontally. In order to prevent the downwards slipping of m2 between m1 and m3 if coefficient of friction between m2 and m3 is μ and all the other surface are smooth, the minimum value of F :
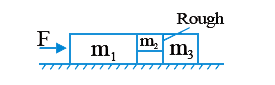
View SolutionIn the figure , masses m1,m2 and M are 20 kg , 5 kg and 50 kg respectively . The coefficient of friction between M and ground is zero . The coefficient of friction between m1 and M and that between m2 and ground is0.4 . The pulleys and the string are massless . The string is perfectly horizontal between P1 and m1 and also between P2 and m2 . The string is perfectly vertical between P1 and P2 . An external horizonal force F is applied to the mass M . (Take g = 10m/s2)
(a) Draw a free body diagram for mass M , clearly showing all the forces .
(b) Let the magnitude of the force of friction between m1 and M be f1 and that between m2 and ground be f2 . For a particular F it is found that f1=2f2 . Find f1 and f2 . Write down equation of motion of all the masses . Find F , tension in the string and acceleration of the masses .

View SolutionIn the figure masses m1,m2andM are 20 kg, 5 kg and 50 kg, respectively. The co-efficient of friction between M and ground is zero. The co-efficient of friction between m1andM and that between m2 and ground is 0.3. The pulleys and the string are massless.
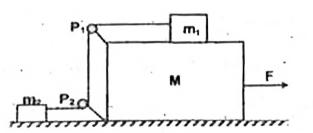
The string is perfectly horizontal between P1 and m1 and also between P2andm2. The string is perfectly vertical between P1andP2. An external horizontal force F is applied to the mass M. Take g=10m/s2.
(a) Draw a free body diagram for mass M, clearly showing all the forces.
(b) Let the magnitude of the force of friction between m1andM be f1 and that between m2 and ground be f2. For a particular F, it is found that f1=2f2. Find f1andf2. Write down equations of motion of all the masses. Find F, tension in the string and accelerations of the masses.
View SolutionIf, in Q.19, coefficient of friction between m1 and the wall is μ,and f1 and f2 are respectively, the force of friction on m1 and m2, then :
View Solution
