AS chain of length l and mass m lies o the surface of a smooth sphere of radius R>l with one end tied to the top of the sphere. a.Find the gravitational potential energy of the chain with reference level at the centre of the sphere. B. suppose the chin is released and slides down the sphere. Find the kinetic eneergy of the chain, when it has slid through an angle θ c. find the tangential acceleration dvdt of the chain when the chain starts sliding down.Solution in Tamil
The correct Answer is:A, B
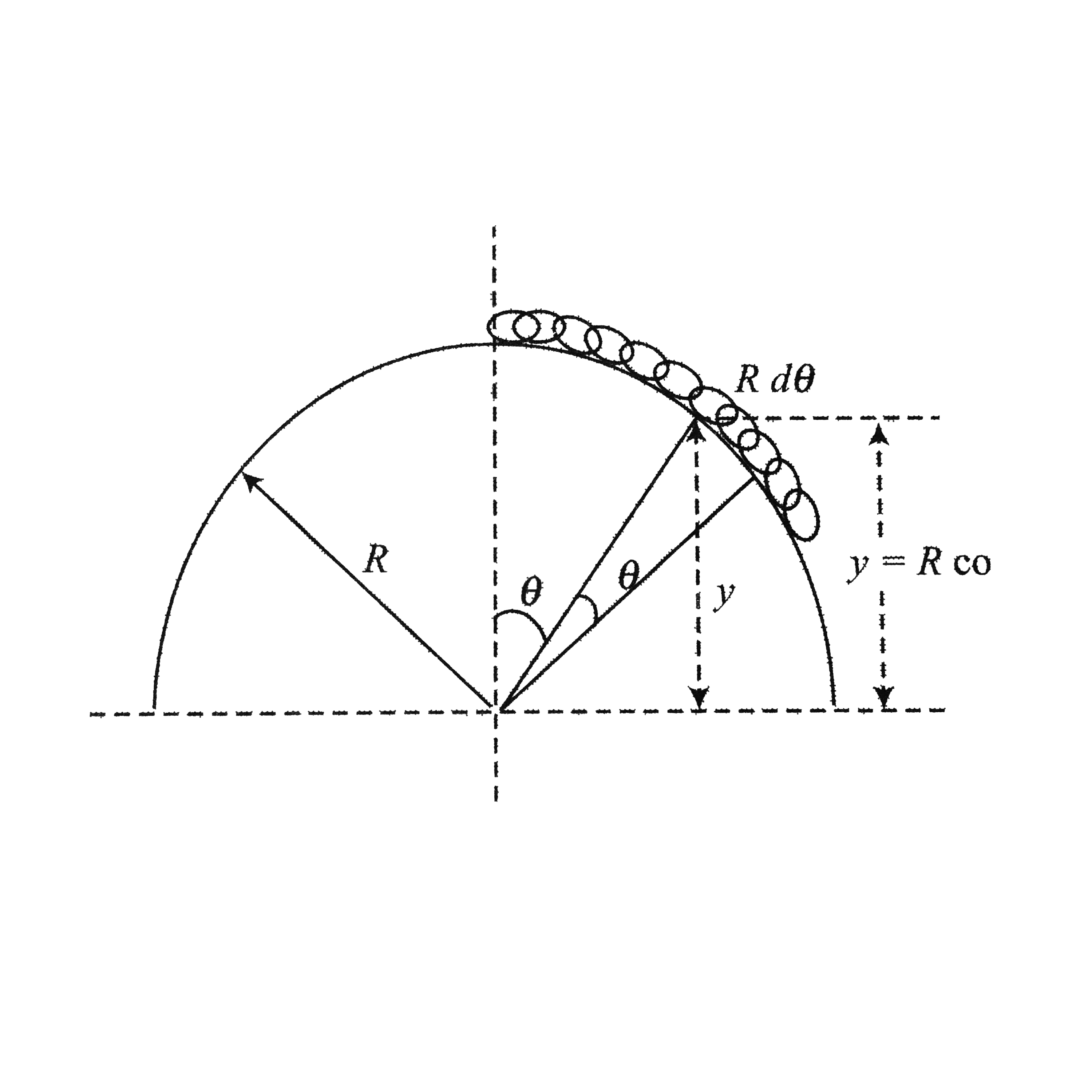
Let us consider a small element which makes angle dthη at the centre.
∴dm=ρ(mL)Rdthη
a. Gravitational potential energy of dm with respect to centre of the sphere
(dm)gRcosθ
=(mgL)R2cosθdthη<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/HCV_VOL1_C08_E01_100_S01.pngwh=80%mx-autosty≤=background:white;><br>:. total G.P.E. =int_0^(L/R) mg R^2/L costheta dtheta<br>=(L/R)<br>=(mR^2g)/L[sintheta][theta=L/R]<br>=(mR^2g)/Lsin(L/R)<br>b.whenthecha∈isre≤asedomrestandslsdownthrughan∠θ,theK.E.ofthecha∈isgivenbyK.E.=chan≥ispotentiale≠rgy.<br>(mR^2g)/L sin (L/R)-int(gR^2)/L costheta dtheta<br>=(mR^2g)/L[sin(L/R)+sintehta-sin{theta+(L/R)}]<br>c.SinceK.E. =1/2 mv^2<br>=(mR^2g)/L[sin(L/R)]<br>tak∈gderivativeof⊥hsswithrespect→t,<br>(1/2)xx2xxx(dv)/(dt)<br>=(R^2g)/L[costheta-(dtheta)/dt)-cos(theta+L/R)(dtheta)/(dt)]<br>:. [R-(dtheta)/(dt) (dv)/dt<br>=(R^2g)/Lxx(dtheta)/(dt)[costhet-cos(theta+L/R)]<br>(becausev=Rω=Rdthηdt)
∴dvdt=RgL[cosθ−cos(θ+LR)]
When the chain strrts sliding down,
θ=0
∴dvdt=RgL[1−cos(LR)]
Topper's Solved these Questions
Similar Questions
A heavy stone is thrown from a cliff of height h with a speed v. The stone will hit the ground with maximum speed if it is thrown
View SolutionA wave pulse passing on a string with speed of 40cms−1 in the negative x direction has its maximum at x=0 at t=0. Where will this maximum be located at t=5s?
View SolutionA chain of length l and mass m lies of the surface of a smooth hemisphere of radius R>l with one end tied to the top of the hemisphere. Taking base of the hemisphere as reference line, find the gravitational potential energy of the chain.
View SolutionA chain of length l is placed on a smooth spherical surface of radius R with one of its ends fixed at the top of the sphere. What will be the acceleration w of each element of the chain when its upper end is released? It is assumed that the length of the chain llt1/2piR .
View SolutionA uniform chain of mass m and length llt(piR)/(2) is placed on a smooth hemisphere of radius R with on of its ends fixed at the top of the sphere. (a) Find the gravitational potential energy of chain assuming base of hemisphere as reference. (b) what will be the tangential acceleraion of the chain when it starts sliding down. (c ) If the chain slides down the sphere, find the kinetic energy of the chain when it has slipped through an angle beta .
View SolutionChain of mass M length L kept on rough sphere. mu is coefficient if friction between sphere and chain F is minimum force required to slide chain
View SolutionA chain of length l = pi R//4 is placed. On a smooth hemispherical surface of radius R with one of its ends fixed at the top of the sphere. Mass of chain is sqrt(pi kg) and R = 1m.(g = 10 m//s^(2)) . The gravitational potential energy of the chain considering reference level at the base of hemisphere is
View SolutionA chain of length l=πR/4 is placed. On a smooth hemispherical surface of radius R with one of its ends fixed at the top of the sphere. Mass of chain is √πkg and R=1m.(g=10m/s2).
If the chain sliped down the sphere, kinetic energy of the chain when it has sliped through an angle θ=π4.
View SolutionA chain of length l=πR/4 is placed. On a smooth hemispherical surface of radius R with one of its ends fixed at the top of the sphere. Mass of chain is √πkg and R=1m.(g=10m/s2).
The tangential acceleration of the chain when its starts sliding down.
View Solutionm द्रव्यमान तथा l लंबाई की एक चेन R त्रिज्या के चिकने गोले की सतह पर रखी हुई हैं , चेन का एक सिरा गोले के उच्चतम बिंदु पर पकड़कर रखा हुआ हैं । R का मान l से अधिक हैं । गोले के केंद्र पर स्थितिज ऊर्जा को शून्य मानते हुए दी गई स्थिति में चेन की गुरुत्वीय स्थितिज ऊर्जा ज्ञात करें ।
View Solutionm द्रव्यमान तथा l लंबाई की एक चेन R त्रिज्या के चिकने गोले की सतह पर रखी हुई हैं , चेन का एक सिरा गोले के उच्चतम बिंदु पर पकड़कर रखा हुआ हैं । R का मान l से अधिक हैं । मान लीजिए कि चेन छोड़ दी जाती हैं तथा यह गोले पर नीचे की ओर फिसलने लगती हैं । जब यह कोण θ कोण फिसल जाती हैं , तो चेन की गतिज ऊर्जा ज्ञात करें ।
View Solutionm द्रव्यमान तथा l लंबाई की एक चेन R त्रिज्या के चिकने गोले की सतह पर रखी हुई हैं , चेन का एक सिरा गोले के उच्चतम बिंदु पर पकड़कर रखा हुआ हैं । R का मान l से अधिक हैं । जब चेन फिसलना प्रारंभ करती हैं , उस समय चेन का स्पर्शरेखीय त्वरण dvdt ज्ञात कीजिए ।
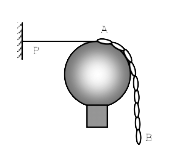
View SolutionA chain of mass per unit length λ and length 1.5 m rests on a fixed smooth sphere of radius R=2πm such that A end of chain is at the top of sphere while the other end is hanging freely. Chain is held stationary by a horizontal thread PA. The tension in the thread is:
View SolutionA uniform chain of length l and mass m lies on the surface of a smooth hemisphere of radius R(Rgtl) with one end tied to the top of the hemisphere as shown in the figure. Gravitational potential energy of the chain with respect to the base of the hemisphere is
View SolutionA chain of length 1 and mass m lies on the surface of a smooth sphere of radius R>1 with one end tied to the top of the space.
Find the gravitational energy of the chain with reference level at the centre of the sphere
View SolutionA chain of length 1 and mass m lies on the surface of a smooth sphere of radius R>1 with one end tied to the top of the space.
Suppose the chain is released and slides down the sphere. Find the kinetic energy of the chain, when it has slid through an angle θ.
View Solution