Chain of mass $M$ length $L$ kept on rough sphere. $μ$ is coefficient if friction between sphere and chain $F$ is minimum force required to slide chain

A

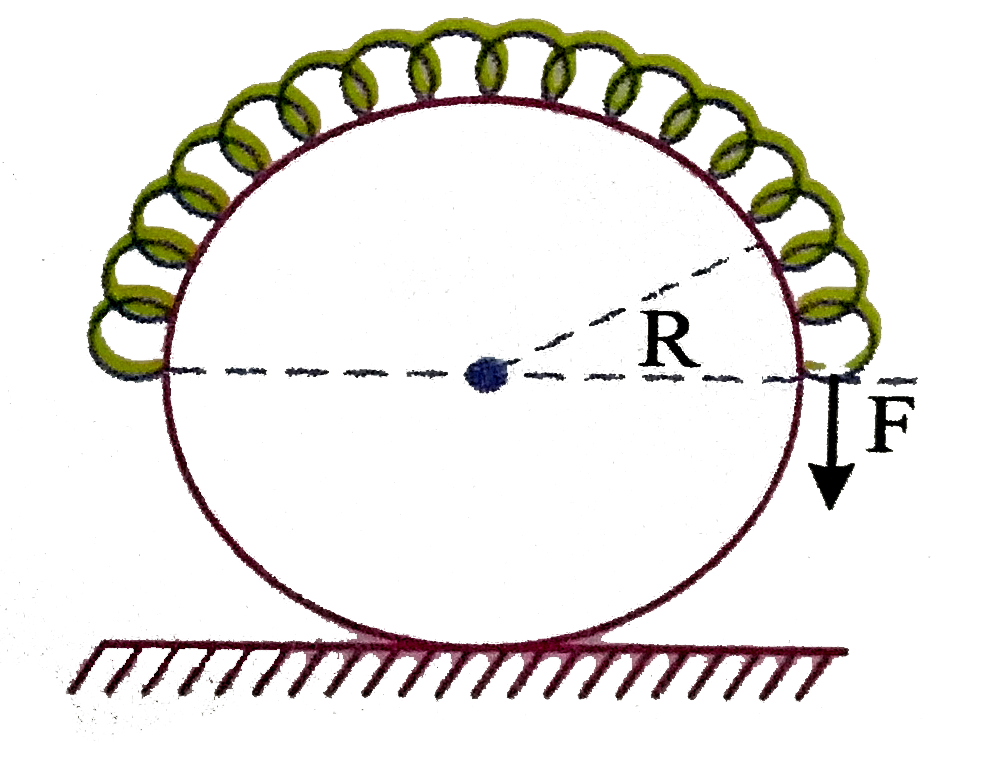
$\frac{2 μ M g}{π}$

B

$μ M g$

C

$< \frac{2 μ M g}{π}$

D

$2 μ M g$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

If we consider

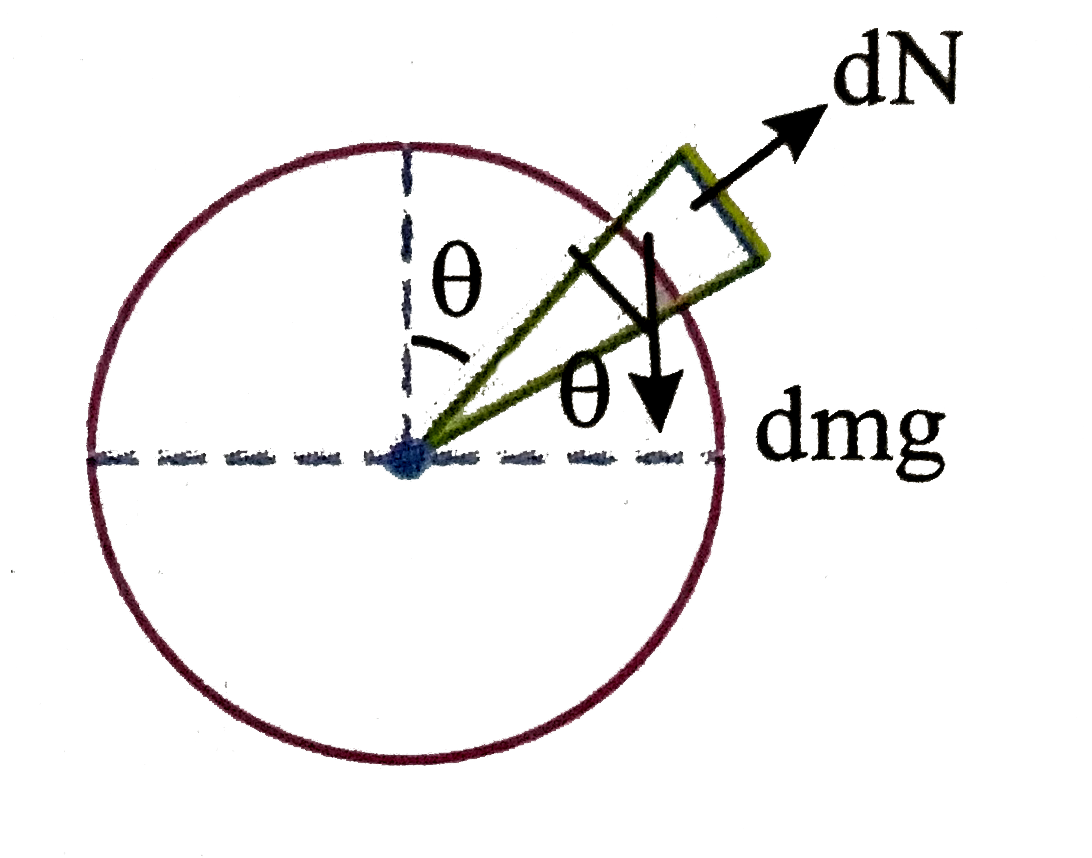
$F = μ d N = μ \frac{M}{π} g π / 2 \int \frac{π}{2} cos θ d θ$
$d N = Δ m g cos θ$
$F = \frac{2 μ M g}{π}$ but $d N = Δ m g cos θ + T d θ$
So the frictional force $F > \frac{2 μ m g}{π}$ hence $F > \frac{2 μ m g}{π}$

Updated on:21/07/2023

|

Class 11 PHYSICS FRICTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

A solid sphere of mass $m$ is lying at rest on a rough horizontal surface. The coefficient of friction between the ground and sphere is $μ$ . The maximum value of $F$ , so that the sphere will not slip, is equal to

A $\frac{7}{5} μ m g$
B $\frac{4}{7} μ m g$
C $\frac{5}{7} μ m g$
D $\frac{7}{2} μ m g$
A solid sphere of mass $m$ is lying at rest on a rough horizontal surface. The coefficient of friction between the ground and sphere is $μ$ . The maximum value of $F$ , so that the sphere will not slip, is equal to

A $\frac{7}{5} μ m g$
B $\frac{4}{7} μ m g$
C $\frac{5}{7} μ m g$
D $\frac{7}{2} μ m g$
A uniform chain of mass m and length I is kept on the table with a part of it overhanging (see figure). If the coefficient of friction between the table and the chain is $1 / 3$ then find the maximum length of the chain that can overhang such that the chain remain in equilibrium.

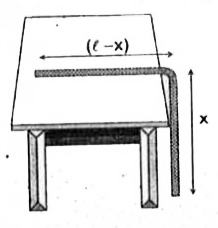A $L / 3$
B $L / 2$
C $L / 4$
D $2 L / 3$

NARAYNA-FRICTION-Passage type of questions I

Home
Ask Doubt
Profile