A block of mass m=1/3 kg is kept on a rough horizontal plane. Friction coefficient is μ=0.75. The work done by minimum force required to drag to the block along the plane by a distance 5m is :-
8 J
4 J
2 J
6 J
The correct Answer is:A
To solve the problem, we need to find the work done by the minimum force required to drag a block of mass m=13 kg on a rough horizontal plane with a coefficient of friction μ=0.75 over a distance of 5 m.
1. Identify the Forces Acting on the Block:
- The weight of the block W=mg acts downwards.
- The normal force R acts upwards.
- The frictional force Ff acts opposite to the direction of motion, given by Ff=μR.
- The applied force P is what we need to determine.
2. Calculate the Weight of the Block:
W=mg=13 kg×10 m/s2=103 N
3. Set Up the Equation for Normal Force:
Since the block is on a horizontal plane, the normal force R can be expressed as:
R=W=103 N
4. Calculate the Frictional Force:
The frictional force is given by:
Ff=μR=0.75×103=7.53=2.5 N
5. Determine the Minimum Force Required to Overcome Friction:
The minimum force P required to drag the block is equal to the frictional force when the block is just about to move:
P=Ff=2.5 N
6. Calculate the Work Done by the Force:
Work done W by the force P when moving the block a distance d=5 m is given by:
W=P×d=2.5 N×5 m=12.5 J
Final Answer:
The work done by the minimum force required to drag the block along the plane by a distance of 5 m is 12.5 Joules.
---
- The weight of the block W=mg acts downwards.
- The normal force R acts upwards.
- The frictional force Ff acts opposite to the direction of motion, given by Ff=μR.
- The applied force P is what we need to determine.
W=mg=13 kg×10 m/s2=103 N
Since the block is on a horizontal plane, the normal force R can be expressed as:
R=W=103 N
The frictional force is given by:
Ff=μR=0.75×103=7.53=2.5 N
The minimum force P required to drag the block is equal to the frictional force when the block is just about to move:
P=Ff=2.5 N
Work done W by the force P when moving the block a distance d=5 m is given by:
W=P×d=2.5 N×5 m=12.5 J
The work done by the minimum force required to drag the block along the plane by a distance of 5 m is 12.5 Joules.
Topper's Solved these Questions
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
- TEST PAPER 1BOOK - ALLENCHAPTER - TEST PAPER 1EXERCISE - PHYSICS
11 Videos
Similar Questions
A block of mass m is kept on a horizontal table. If the static friction coefficient is μ., find the frictional force acting on the block.
View SolutionA block of mass 10 kg rests on a rough inclined plane of inclination 45∘ with the horizontal. What minimum force is required to just move the block up the inclined plane. Given μs=0.5andg=10ms−2.
View Solution
Knowledge Check
A block of mass 2 kg is kept on a rough horizontal floor an pulled with a force F. If the coefficient of friction is 0.5. then the minimum force required to move the block is :-
 A10 NB10011NC1008ND20 N
A10 NB10011NC1008ND20 NA block of mass m is at rest on a rough inclined plane, whose friction coefficient is μ. Net force exerted by surface on block is :-
AmgBmg sin θCμmgcosθDμmgsinθA block of mass m lying on a rough horizontal surface of friction coefficient μ is pulled by a force F as shown , the limiting friction between the block and surface will be
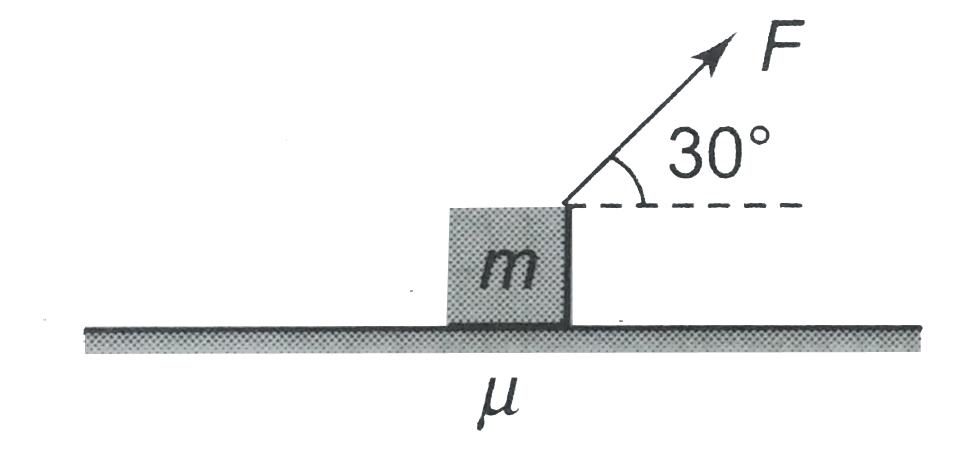 AμmgBμ(mg+F2)Cμ(mg−F2)Dμ(mg−√3F2)
AμmgBμ(mg+F2)Cμ(mg−F2)Dμ(mg−√3F2)
A block of mass m=3kg slides on a rough inclined plane of cofficient of friction 0.2 Find the resultant force offered by the plane on the block

View SolutionA block of mass 5kg is placed on a rough horizontal plane.A time dependent horizontal force F=(t2+2t) N acts on the block. The friction force between the block and the plane at t=3s is (μ=0.4)
View SolutionA block of mass 10kg is placed on a rough horizontal surface having coefficient of friction μ=0.5 . If a horizontal force of 100N is acting on it, then acceleration of the will be.
View SolutionA block of mass m is pulled by a constant powert P placed on a rough horizontal plane. The friction coefficient the block and surface is μ. The maximum velocity of the block is.
View SolutionA block of mass 4 kg is kept on a rough horizontal surface. The coefficient of static friction is 0.8. If a force of 19 N is applied on the block parallel to the floor, then the force of friction between the block and floor is
View Solution
