The potential energy (in joules ) function of a particle in a region of space is given as:
U=(2x2+3y2+2x)
Here x,y and z are in metres. Find the maginitude of x compenent of force ( in newton) acting on the particle at point P ( 1m, 2m, 3m).
2
3
0
4
The correct Answer is:A
Step by step video, text & image solution for The potential energy (in joules ) function of a particle in a region of space is given as: U=(2x^(2)+3y^(2)+2x) Here x,y and z are in metres. Find the maginitude of x compenent of force ( in newton) acting on the particle at point P ( 1m, 2m, 3m). by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
- TEST PAPER 1BOOK - ALLENCHAPTER - TEST PAPER 1EXERCISE - PHYSICS
11 Videos
Similar Questions
The potential energy function of a particle in a region of space is given as U=(2xy+yz) J Here x,y and z are in metre. Find the force acting on the particle at a general point P(x,y,z).
View SolutionIf the potential energy function of a particle is given by U=−(x2+y2+z2)J, whre x,y and z are in meters. Find the force acting on the particle at point A(1m,3m,5m).
View Solution
Knowledge Check
The potential energy of a particle of mass 1 kg in a conservative field is given as U=(3x2y2+6x) J, where x and y are measured in meter. Initially particle is at (1,1) & at rest then:
AInitial acceleration of particle is 6√5ms2BWork done to slowly bring the particle to origin is 9 JCWork done to slowly bring the particle to origin is −9 JDIf particle is left free it moves in straight lineThe electric potential in a region is given by V=(2x2−3y) volt where x and y are in meters. The electric field intensity at a point (0,3m,5m) is
A−6ˆiN/CB3ˆjN/CC−3ˆjN/CDZeroA particle of mass 1 kg is moving along the line y = x + 2 (here x and y are in metres) with speed 2 m/s. The magnitude of angular momentum of particle about its origin is
A4kgm2s−1B2√2kgm2s−1C4√2kgm2s−1D2kgm2s−1
The potential energy of a partical of mass 2kg moving in y−z plane is given by U=(−3y+4z)J where y and z are in metre. The magnitude of force ( in newton ) on the particle is :
View SolutionTrajectory of a particle in a projectile motion is given as y=x−x280. Here x and y are in metre. For this projectile motion the following with g=10m/s2.
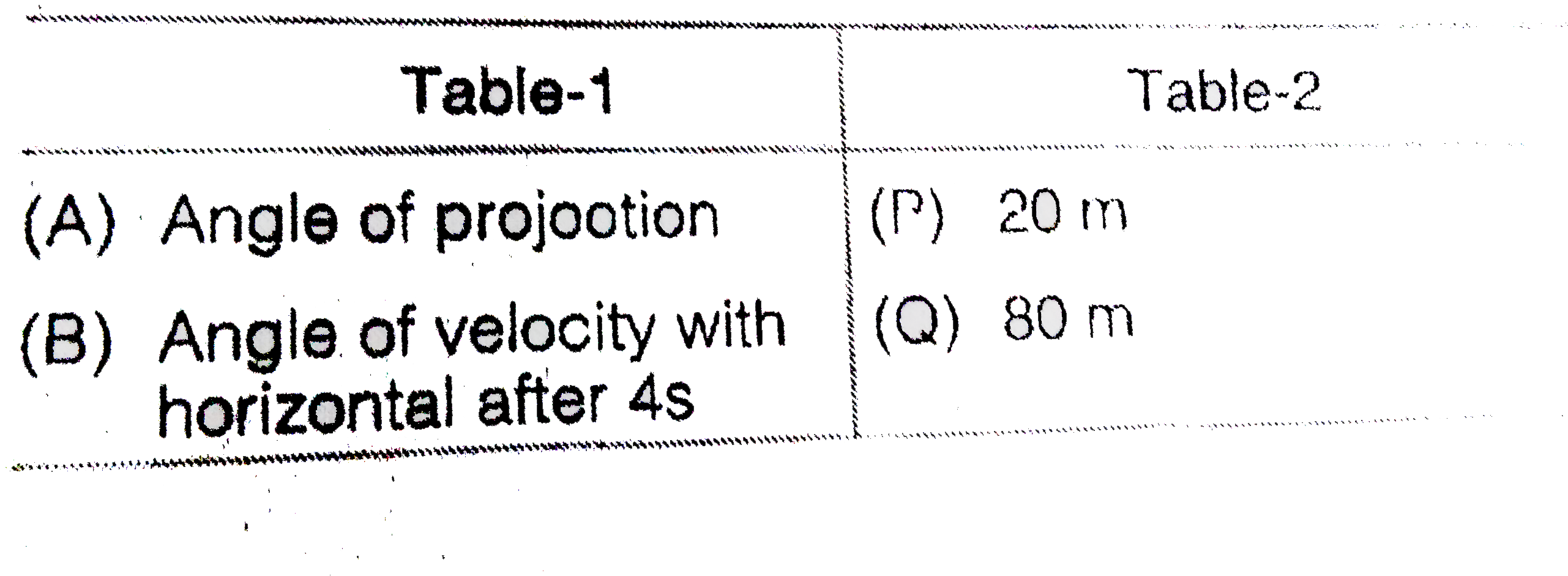
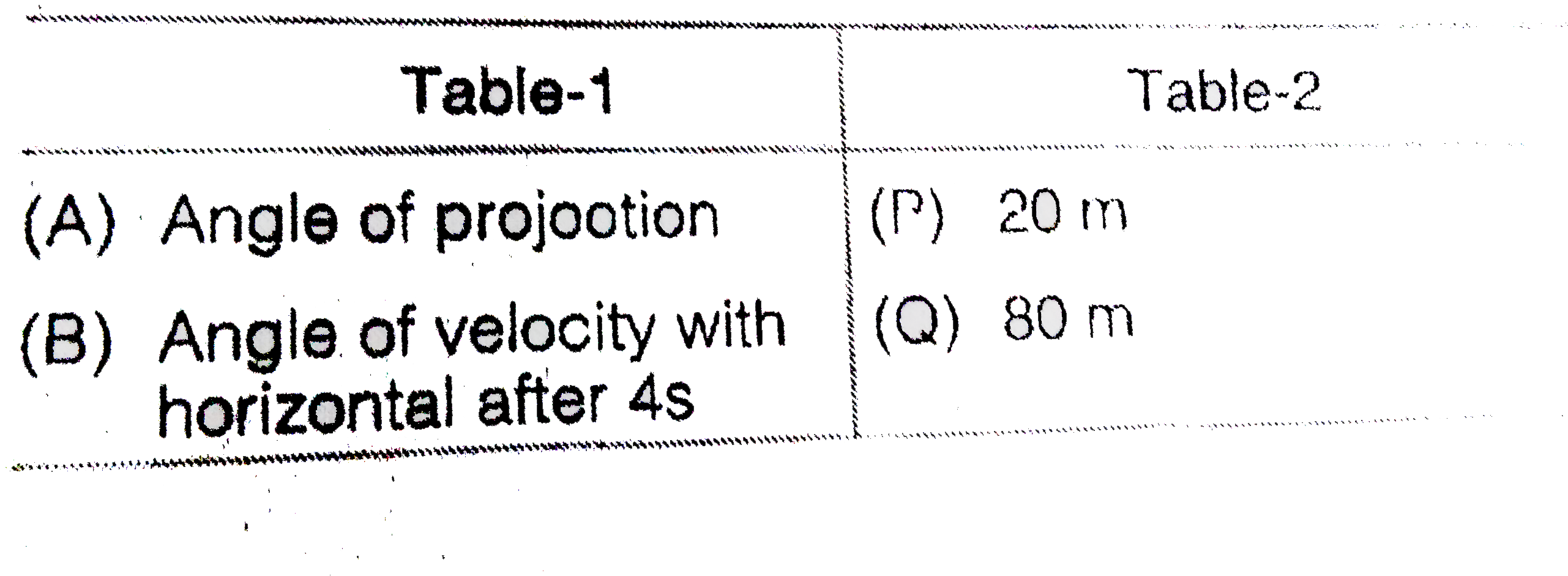
View SolutionThe potential energy of a particle under a conservative force is given by U(x)=(x2−3x) J. The equilibrium position of the particle is at
View SolutionElectric potential in a region of space is given by V=(x2+y2+z2)V. What will be electric field intensity at a point P(-1m, 2m, -3m)?
View SolutionThe potential energy of a particle of mass 2kg moving along the x-axis is given by U(x)=4x2−2x3( where U is in joules and x is in meters). The kinetic energy of the particle is maximum at
View Solution
