A heavy particle is usspended by a 1.5 m long string . It is given a horizontal velocityof √57ms. a. Find the angle made by the string with the upward vertical, when it becomes slack. B. Find the speed of the particle at this instant. c.Find the maximum height reached by the particle over the point of suspension. Take g=10ms2Solution in Tamil
The correct Answer is:A, B, C
L=1.5m,u=√57msec
a. mgcosθ=mv2L
v2=Lgcosθ
change in K.E.= work done
12mv2−12μ2=mgh
→v2−57=−2×1.5g(1+cosθ) ……….ii
→v2=57−3g(1+cosθ)
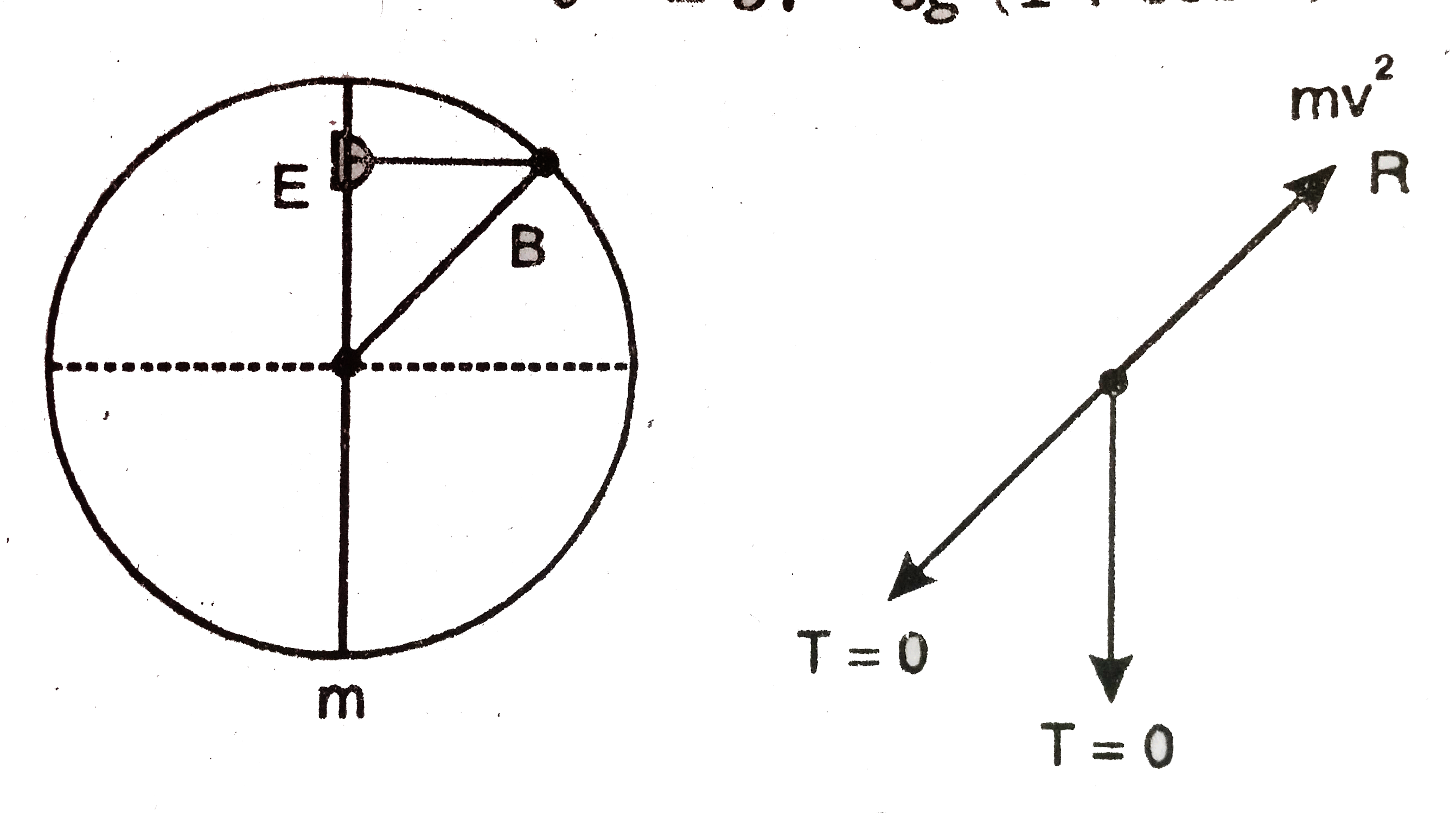
Putting the value of v from equaltion i.
15cosθ−57−3g(1+cosθ)
→15cosθ=57−30−30cosθ
→45cosθ=27
→cosθ=35
→θ=cos−135=530
b. v=√57−3g(1+cosθ) from equation i
√9=esec.<br>c.asthestr∈gbecomeslackatp∮B,thepartic≤will⋆tmakignprojectionti≤motion<br>H=OF+DC<br>=1.5costheta+(u^2sin^2theta)/(2g)<br>(1.5)xx3/5xx(9xx(0.8)^2)/(2xx10)<br>1.2m
Topper's Solved these Questions
Similar Questions
A heavy stone is thrown from a cliff of height h with a speed v. The stone will hit the ground with maximum speed if it is thrown
View SolutionA wave pulse passing on a string with speed of 40cms−1 in the negative x direction has its maximum at x=0 at t=0. Where will this maximum be located at t=5s?
View SolutionA ball is projected vertically upward with speed of 50 m/s. Find a. the maximum height, b. the time to reach themaximum height, c. the speed at half the maximum height. Take g= 10 m/s^2 .
View SolutionFind the maximum height reached by a particle which is thrown vertically upwards with the velocity of 20 m//s (take g= 10 m//s^(2) ).
View SolutionA heavy particle hanging from a fixed point by a light inextensible string of length l is projected horizontally with speed (gl) . Then the speed of the particle and the inclination of the string to the vertical at the instant of the motion when the tension in the string equal the weight of the particle-
View SolutionA particle is projected vertically upward in vacum with a speed 40m//s then velocity of particle when it reaches at maximum height 2s before, is (Take g=10m//s )
View SolutionA particle is thrown vertically upward. Its velocity at half of the height is 10 m/s. Then the maximum height attained by it : -
(g=10m/s2)
View Solution1.5 लंबी डोरी से एक भारी कण लटाकाया गया हैं । इसको √24m/s का क्षैतिज वेग प्रदान किया गया हैं । डोरी के व्दारा ऊपर की ओर ऊर्ध्वाधर से बनाया गया कोण ज्ञात कीजिए जब डोरी ढीली पड़ जाती हैं ।
View Solution1.5 लंबी डोरी से एक भारी कण लटाकाया गया हैं । इसको √57m/s का क्षैतिज वेग प्रदान किया गया हैं ।ऊर्ध्वाधर से 300 इस क्षण पर कण की चाल ज्ञात कीजिए ।
View Solution1.5 लंबी डोरी से एक भारी कण लटाकाया गया हैं । इसको √24m/s का क्षैतिज वेग प्रदान किया गया हैं । निलंबन - बिंदु से कण की अधिकतम ऊँचाई ज्ञात कीजिए । (g=10m/s2)
View SolutionA heavy particle hangs from a point O, by a string of length a. It is projected horizontally with a velocity u = sqrt((2 + sqrt(3))ag) . The angle with the downward vertical, string makes where string becomes slack is :
View SolutionA particle is thrown vertically upwards its velocity at half of the height is 10 m/s then the maximum height attained by it is (g=10m/s2)
View SolutionBob of the pendulum is at its bottom most point when it is given horizontal velocity sqrt(57) m/s . Length of the string is 1.5 m . (i) Find maximum height attained by the bob above its lowest point . (b) What will be the answer to part (a) if intial velocity given s sqrt(95) m/s ?
View SolutionA ball is projected vertically upward with speed of 50 m/s. Find a. the maximum height, b. the time to reach the maximum height, c. the speed at half the maximum height. Take g= 10 m/s^2 .
View SolutionA heavy particle hanging from a fixed point by a light inextensible string of length l is projected horizontally with speed (gl) . Then the speed of the particle and the inclination of the string to the vertical at the instant of the motion when the tension in the string equal the weight of the particle-
View SolutionA particle is thrown vertically upward. Its velocity at half of the height is 10 m/s. Then the maximum height attained by it : -
(g=10m/s2)
View Solution