A wave pulse passing on a string with speed of 40cms−1 in the negative x direction has its maximum at x=0 at t=0. Where will this maximum be located at t=5s?Solution in Tamil
The correct Answer is:A, B
v=40cmsec
As velocity of a wave is constant location of maximum after 5 sec.
=40×5
=200cmalong¬ativex−aξs.<br>rarr at x=-2m
Topper's Solved these Questions
Similar Questions
A mechanical wave propagastes in a medium along the X-axis. The particles of the medium moves in what direction?
View SolutionThe gravitational force acting on a particle of 1 g due to a similar particle is equal to 6.67×10−17N. Calculate the separation between the particles.
View SolutionThe mass of a cyclist together with the bicycle is 90 kg. Calculate the work done by cyclist if the speed increases from 6km/h to 12 km/h.
View SolutionA wave is propgting of a long stretched string along its length taken as the positive x-axis. The wave equation is given as
y=y0e−(tT−xλ)^2
where y0=4mm,T=1.0sandλ=4cm. d. Find the velocity of the particle t x=0. c. Find the function g(x) giving the shape of the string t t=0. d. Plot the shape g(x) of the string at t=0. e. Plot of the shape of the string at t=5s.
View SolutionThe equation of a wve travelling on a string stretched along the X-axis is given by
y=Ad−(xatT)2
a. Write the dimensions of A, a and T. b. Find the wave speed. c.In which direction is the wave travelling? d.Where is the maximum of the pulse located at t=T?Att=2T?
View SolutionFigure shows a wave pulse at t=0. The pulse moves to the right with a speed of 10cms^-1. Sketch the shape of the string at t=s, 2s and 3s.

View SolutionThe equation of a wave travelling on a string stretched along the X-axis is given by
y=Ae(−xa+tT)2
(a) Write the dimensions of A, a and T.
(b) Find the wave speed.
(c) In which direction is the wave travelling?
(d) Where is the maximum of the pulse located at t=T and at t=2T?
View SolutionShows the shape of a progressive wave at time t=0. after a time t=(1)/(80), the particle at the origin has its maximum negative displacement.if the wave speed is 80 units maximum negative displacement. If the wave speed is 80 units, then find the equation of the progressive wave.
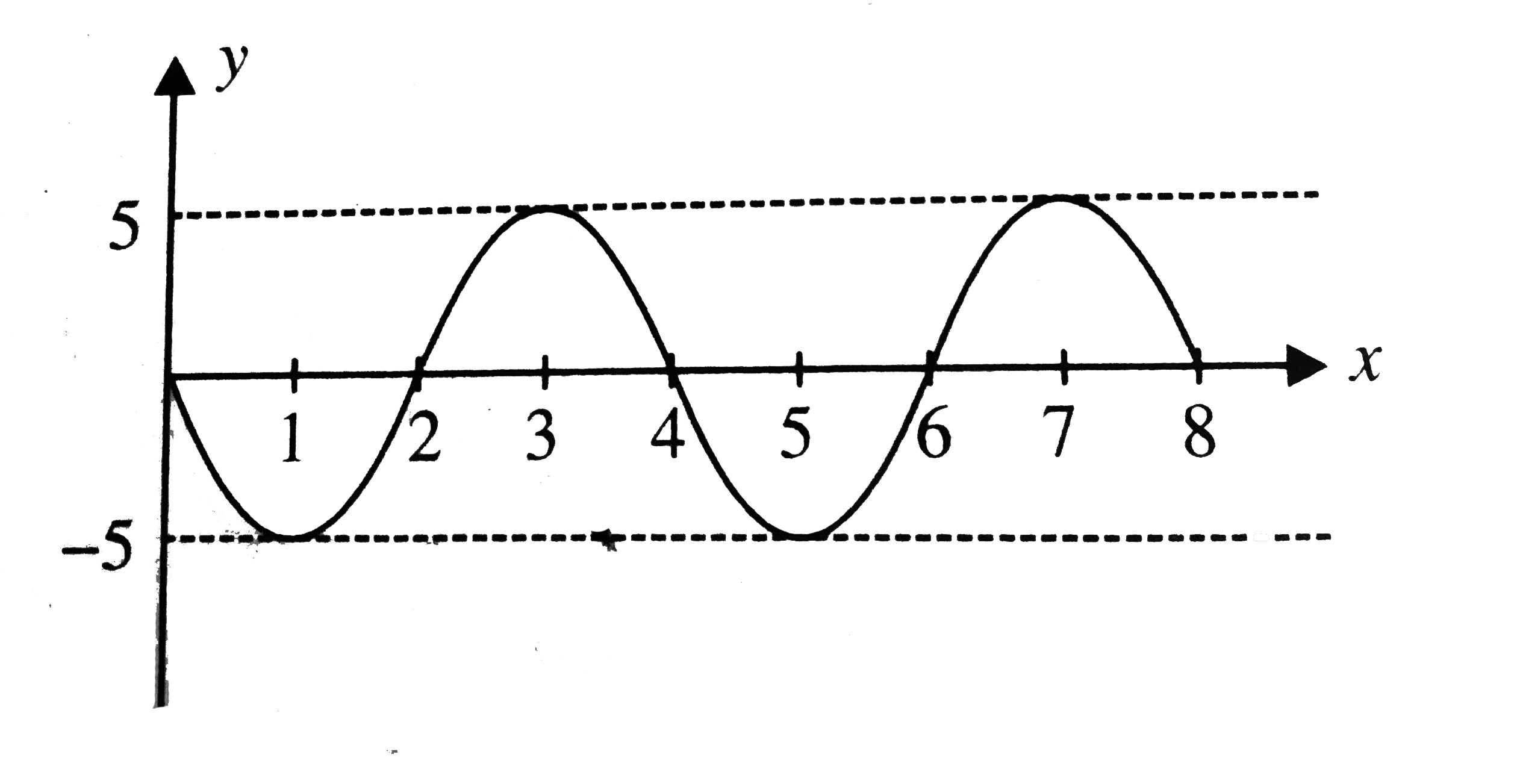 .
.
View SolutionA wave pulse moving along the x axis is represented by the wave funcation
y(x,t)=2(x−3t)2+1
where x and y are measured in cm and t is in seconds.
(i) in which direction is the wave moving ?
(ii) Find speed of the wave.
(iii) Plot the waveform at t=0,t=2s.
View Solutionx(x,t)=0.8[(4x+5t)2+5], represents a moving pulse where x and y are in metre and t is in second. Find
(i) The direction of wave propagation.
(ii) The wave speed.
(iii) The maximum displacement from the mean position (i.e., the aplitude of the wave).
(iv). Whether the wave pulse is symmetric or not.
View Solutionएक डोरी पर 40cm/s की चाल से एक तरंगिका जा रही है । t=0 पर इस तरंगिका का महत्तम बिंदु पर है । यह महत्तम बिंदु t=5s पर कहाँ पर होगा ?
View SolutionAt t=0 , a transverse were pulse in a wire is described by the function where x and y are in metre. The function y(x, t) that describes this wave equation, if it is travelling in the positive x - direction with a speed of "4.5 m s"^(-1) is
View SolutionThe wave function for the wave pulse is y(x,t)=0.1C3C2+(x−vt)2 with C=4cm at x=0 the displacement y(x,t) is observed to decrease from its maximum value to half of its maximum value in time t=2×10−3s.
View SolutionFigure shows a wave pulse at t=0. The pulse moves to the right with a speed of 10cms^-1. Sketch the shape of the string at t=1s, 2s and 3s.

View SolutionA pulse travelling on a string is represented by the function y=a2(x−vt)2+a2 where a =5 mm v = 20 cm/s where the maximum of pulse is located at t = 0, Is and 2s. Take x = 0 in the middle of the string
View SolutionThe equation of a wave travelling on a string stretched along the X-axis is given by
y=Ae(−xa+tT)2
(a) Write the dimensions of A, a and T.
(b) Find the wave speed.
(c) In which direction is the wave travelling?
(d) Where is the maximum of the pulse located at t=T and at t=2T?
View Solution

