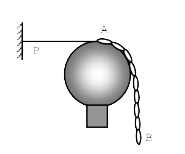
A chain of mass per unit length λ and length 1.5 m rests on a fixed smooth sphere of radius R=2πm such that A end of chain is at the top of sphere while the other end is hanging freely. Chain is held stationary by a horizontal thread PA. The tension in the thread is:
λg(12+2π)
λg(π2+2π)
λg(2π)
None of these
The correct Answer is:A
Length of the hanging part =(1.5−2πR4)=0.5m
∴T1=0.5λg
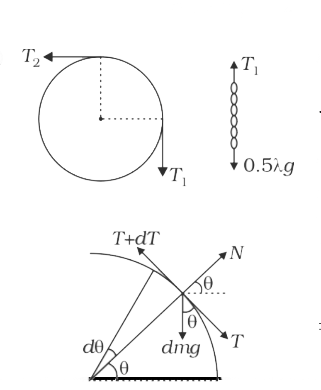
Consider the force diagram of a small mass dm=Rλdθ which subtends angle dθ at the centre and whose position vector with respect to the centre of the sphere makes an angle θ with horizontal.
⇒T+dT=T+(dm)gcosθ,N=(dm)gsinθ
⇒∫T2T1dT=Rλg∫π/20cosθ.dθ
⇒T2=T1+Rλg=0.5λg+2πλg=λg(12+2π)
Similar Questions
A chain of length l and mass m lies of the surface of a smooth hemisphere of radius R>l with one end tied to the top of the hemisphere. Taking base of the hemisphere as reference line, find the gravitational potential energy of the chain.

View SolutionA chain of length l is placed on a smooth spherical surface of radius R with one of its ends fixed at the top of the sphere. What will be the acceleration of the each element of the chain when its upper end is released? It is assumed that the length of the chain l<(πR2).
View Solution
Knowledge Check
A chain of mass m and length l is placed on a table with one-sixth of it hanging freely from the table edge. The amount of work. done to pull the chain on the table is
Amgl/4Bmgl/6Cmgl/72Dmgl/36A chain of mass m and length l is placed on a table with one-sixth of it hanging freely from the table edge. The amount of work. done to pull the chain on the table is
Amgl/4Bmgl/6Cmgl/72Dmgl/36
A uniform chain of mass m and length l<πR2 is placed on a smooth hemisphere of radius R with on of its ends fixed at the top of the sphere.
(a) Find the gravitational potential energy of chain assuming base of hemisphere as reference.
(b) what will be the tangential acceleraion of the chain when it starts sliding down.
(c ) If the chain slides down the sphere, find the kinetic energy of the chain when it has slipped through an angle β.
View SolutionA chain of length l is placed on a smooth spherical surface of radius R with one of its ends fixed at the top of the sphere. What will be the acceleration w of each element of the chain when its upper end is released? It is assumed that the length of the chain l<12πR.
View SolutionAS chain of length l and mass m lies o the surface of a smooth sphere of radius R>l with one end tied to the top of the sphere. a.Find the gravitational potential energy of the chain with reference level at the centre of the sphere. B. suppose the chin is released and slides down the sphere. Find the kinetic eneergy of the chain, when it has slid through an angle θ c. find the tangential acceleration dvdt of the chain when the chain starts sliding down.
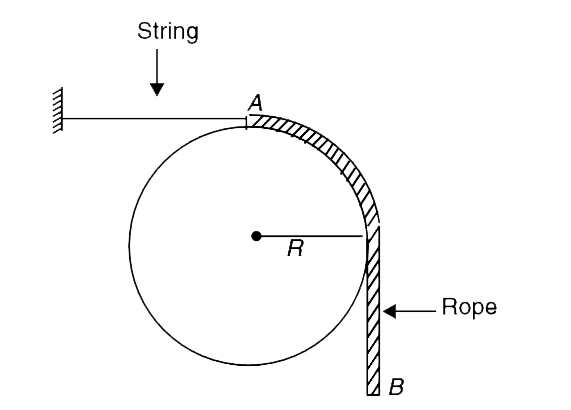
View SolutionA rope of length (π2+1) R has been placed on a smooth sphere of radius R as shown in figure. End A of the rope is at the top of the sphere and end B is overhanging. Mass per unit length of the rope is λ . The horizontal string holding this rope in place can tolerate tension equal to weight of the rope. Find the maximum mass (M0) of a block that can be tied to the end B of the rope so that the string does not break.
View SolutionA chain with uniform mass per unit length lies in a vertical plane along the slope of a smooth hill. The two end of the chain are at same height. If the chain is released from this position find its acceleration.

View SolutionA chain of mass m and length L is over hanging , from the edge of a smooth, horizontal table such that , 3/4th of its length is lying on , the table .The work done in pulling the chain completely , on to the table is
View Solution
