A body with an initial temperature θ1 is allowed to cool in a surrounding which is at a constant temperature of θ0(θ0<θi). Assume that Newton’s law of cooling is obeyed. Let k = constant. The temperature of the body after time t is best expressed by :
T=(T1−T0)e−kt where k = 12σAT30rρc
T=(T1−T0)ln(kt) where k = σAT0mc3
T=T0+(T1−T0)e−kt where k = 12σT30rρc
T=T1e−kt−T0 where k = σT30rρc
The correct Answer is:C
From newton's law of cooling .
σA(T4−T40)=ms(−dTdt)
⇒σ.4ρr2[(T0+ΔT)4−T40]=ρ43πr3c(−dTdt)
⇒(12σT30Prc)(T−T0)=−dTdt
⇒K(T−T0)dt=−dT⇒kt∫0=−T∫T.dTT−T0
⇒T=T0+(T1−T0)e−kt where k = 12σT30rρc
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -03
10 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - ASSERTION-REASON
36 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -01
65 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
A body with an initial temperature θ1 is allowed to cool in a surrounding which is at a constant temperature of θ0(θ<θ1) Assume that Newton's law of cooling is obeyed Let k= constant The temperature of the body after time t is best experssed by .
View SolutionA body cools from a temperature 3T to 2T in 10 minutes. The room temperature is T. Assume that Newton's law of cooling is applicable. The temperature of the body at the end of next 10 minutes will be
View SolutionIf a piece of metal is heated to temperature θ and the allowed to cool in a room which is at temperature θ0, the graph between the temperature T of the metal and time t will be closet to
View SolutionA body cools in a surrounding which is at constant temperature of θ0. Assume that it obeys Newton's law of colling. Its temperature θ is plotted against time t. Tangents are drawn to the curve at the points P(θ=θt) and Q(θ=θ2). These tangents meet the time axis at angles of ϕ2 and ϕ1, as shown
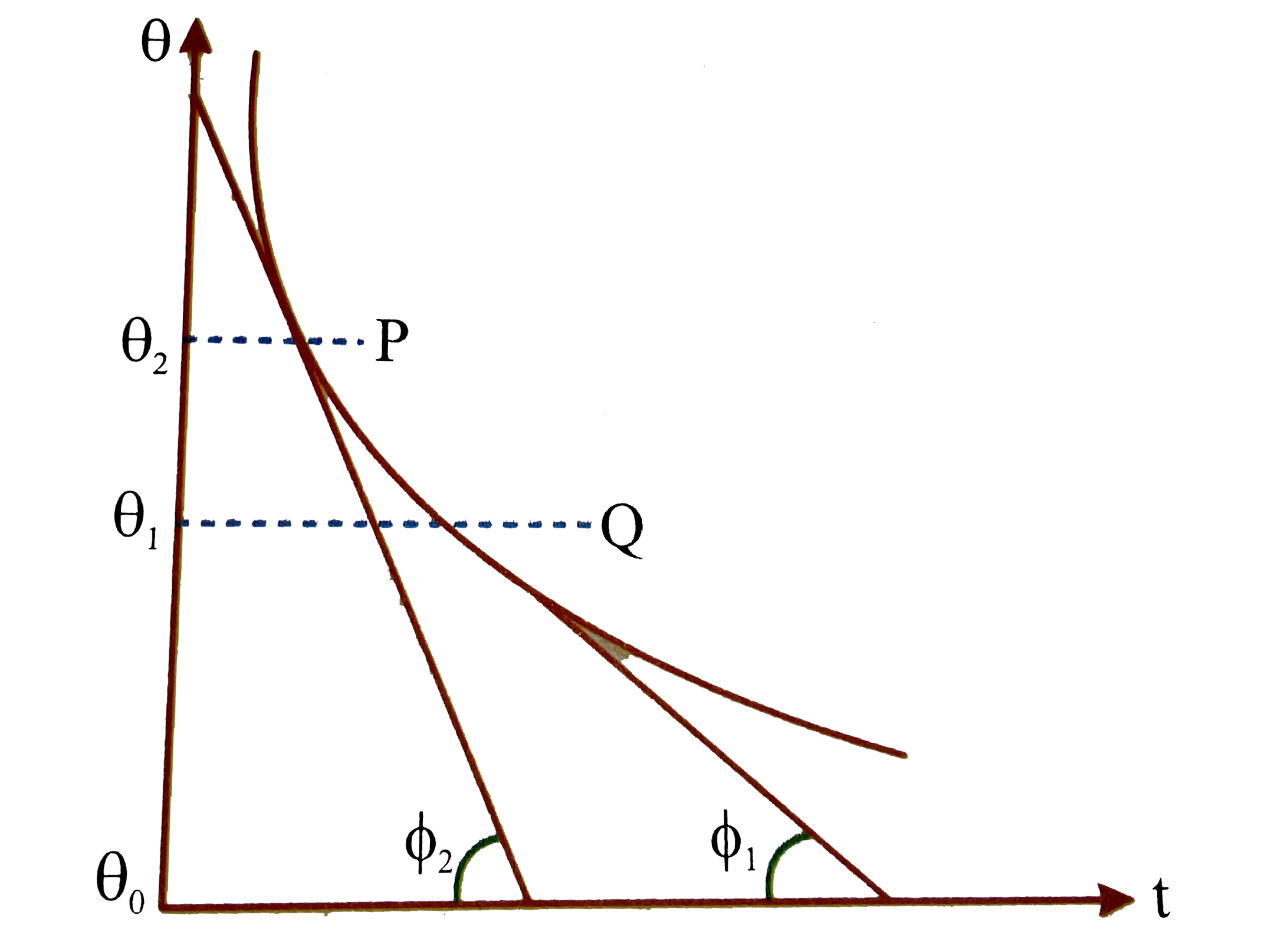
View SolutionA body having mass 2 Kg cools in a surrounding of constant temperature 30∘C. Its heat capacity is 2J/∘C. Initial temperature of the body is 40∘C. Assume Newton's law of cooling is valid. The body cools to 36∘C in 10 minutes.
When the body temperature has reached 36∘C. it is heated again so that it reaches to 40∘C in 10 minutes. Assume that the rate of loss of heat at 38∘C is the average rate of loss for the given time . The total heat required from a heater by the body is :
View SolutionA body cools in a surrounding of constant temperature 30∘C Its heat capacity is 2J/∘C. Initial temeprature of cooling is valid. The body cools to 38∘C in 10 min
The temperature of the body In .∘C denoted by θ. The veriation of θ versus time t is best denoted as
View SolutionIn Newton's law of cooling dθdt=−k(θ−θ0) the constant k is proportional to .
View SolutionThemperature of a body θ is slightly more than the temperature of the surrounding θ0 its rate of cooling (R) versus temperature of body (θ) is plotted its shape would be .
View SolutionFigure shows a large tank of water at a constant temperature θ0 and a small vessel containing a mass m of water at an initial temperature θ1(<θ0). A metal rod of length L, area of cross section A and thermal conductivity K connects the two vessels. Find the time taken for the temperature of the water in the smaller vessel to become θ2(θ1<θ2<θ0) . Specific heat capacity of water is s and all other heat capacities are negligible.

View SolutionA black body of mass 34.38 g and surface area 19.2cm2 is at an intial temperature of 400 K. It is allowed to cool inside an evacuated enclosure kept at constant temperature 300 K. The rate of cooling is 0.04∘C/s. The sepcific heat of the body Jkg−1K−1 is
(Stefan's constant, σ=5.73×10−8Wm−2K−4)
View Solution
