Figure shows a large tank of water at a constant temperature θ0 and a small vessel containing a mass m of water at an initial temperature θ1(<θ0). A metal rod of length L, area of cross section A and thermal conductivity K connects the two vessels. Find the time taken for the temperature of the water in the smaller vessel to become θ2(θ1<θ2<θ0) . Specific heat capacity of water is s and all other heat capacities are negligible.

Suppose, the temperature of the water in the smaller vessel is theta at time t. In the next time interval dt, a heat (DeltaQ) is transferred to it where
ΔQ=KAL(θ0−θ)dt . This heat increases the temperature of the water of mass m to θ+dθwhereDeltaQ=msd theta.From(i)and(ii),<br>KAL(θ0−θ)dt=msdθ . or, dt=LmsKAdθθ0−θ . or, ∫T0dt=LmsKA∫θ2θ1dθθ0−θ . where T is the time requierd for the temperature of the water to become θ2 . Thus, T=LmsKAln(theta_(0)-theta_(1))/(theta_(0)-theta_(2)) .
Topper's Solved these Questions
- HEAT TRANSFERBook:HC VERMA ENGLISHChapter:HEAT TRANSFERExercise:OBJECTIVE I
Explore 10 Videos
- HEAT TRANSFERBook:HC VERMA ENGLISHChapter:HEAT TRANSFERExercise:OBJECTIVE II
Explore 6 Videos
- HEAT TRANSFERBook:HC VERMA ENGLISHChapter:HEAT TRANSFERExercise:QUESTIONS FOR SHORT ANSWER
Explore 11 Videos
- HEAT AND TEMPERATUREBook:HC VERMA ENGLISHChapter:HEAT AND TEMPERATUREExercise:Objective 2
Explore 6 Videos
- INTRODUCTION TO PHYSICSBook:HC VERMA ENGLISHChapter:INTRODUCTION TO PHYSICSExercise:Question for short Answer
Explore 4 Videos
Similar Questions
Figure shown two adiabatic vessels, each containing a mass m of water at different temperature. The ends of a metal rod of length L, area of cross section A and thermal conductivity K, are inserted in the water as shown in the figure. Find the time taken for the difference between the temperature in the vessels to become half of the original value. The specific heat capacity of water is s. Neglect the heat capacity of the rod and the container and any loss of heat to the atmosphere.

View SolutionIntegrate the following functions
∫θ2θ1dθθ−θ0
View SolutionTwo liquids of specific heat ratio 1:2 are at temperature 2θandθ
View SolutionTwo thin metallic spherical shells of radii r1 and r2 (r1<r2) are placed with their centres coinciding. A material of thermal conductivity K is filled in the space between the shells. The inner shells is maintained at temperature θ1 .and the outer shell at temperature θ2 (θ1<θ2). Calculate the rate at which heat flows radially through the material.

View SolutionTwo thin metallic spherical shells of radii r1 and r2 (r1<r2) are placed with their centres coinciding. A material of thermal conductivity K is filled in the space between the shells. The inner shells is maintained at temperature θ1 and the outer shell at temperature θ2 (θ1<θ2). Calculate the rate at which heat flows radially through the material.

View SolutionIf 0<θ<π/2 then .find the least value of tanθ+cotθ
View SolutionTwo materials having coefficients of thermal conductivity '3k' and 'k' and thickness 'd' and '3d' respectively, are joined to form a slab as shown in the figures. The temperatures of the outer surfaces are θ2 and θ1 respectively (θ2>θ2). The temperature at the interface is :
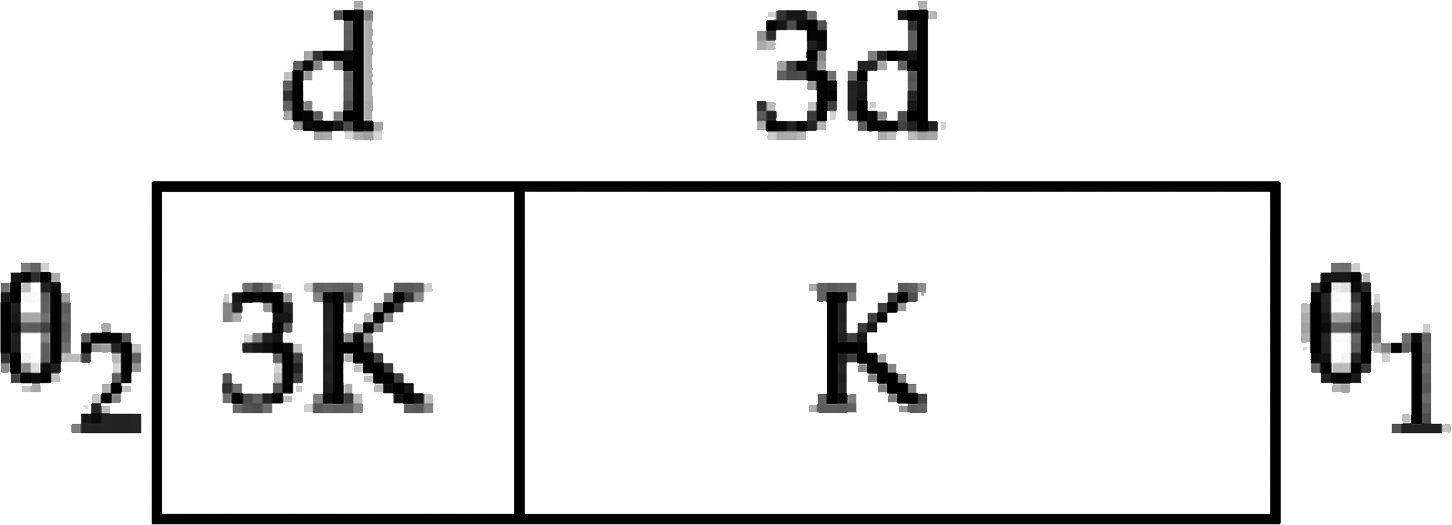
View SolutionFind the rate of heat flow through a cross section of the rod shown in figure (θ2>θ1) . Thermal conductivity of the material of the rod is K.

View SolutionSolve : 5cos2θ+2cos2(θ2)+1=0,−π<θ<π
View SolutionA body with an initial temperature θ1 is allowed to cool in a surrounding which is at a constant temperature of θ0(θ<θ1) Assume that Newton's law of cooling is obeyed Let k= constant The temperature of the body after time t is best experssed by .
View Solution