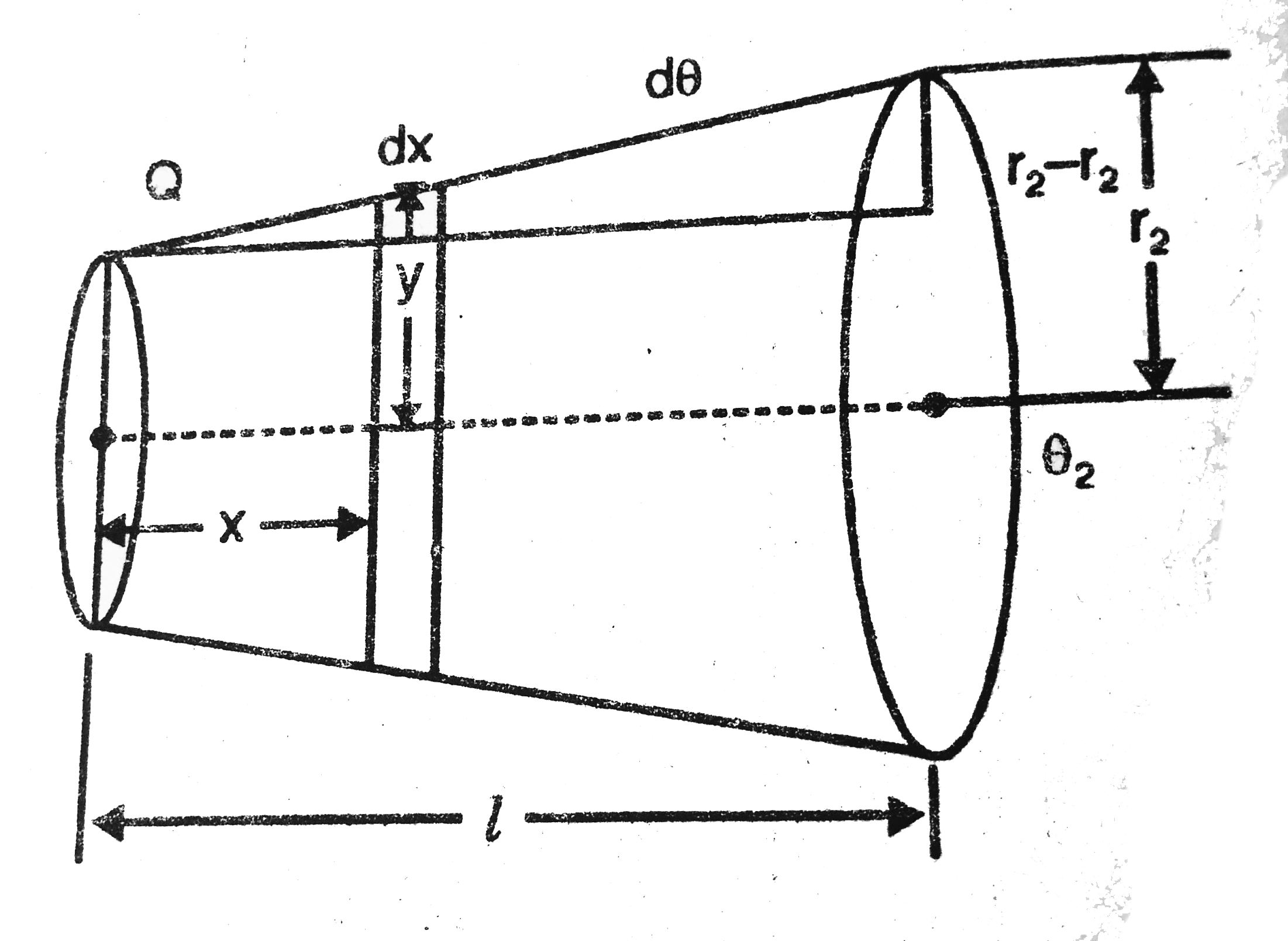
Find the rate of heat flow through a cross section of the rod shown in figure (θ2>θ1) . Thermal conductivity of the material of the rod is K.

The correct Answer is:A, B
TenΦ=r2−r1L=y−r1x
D⇔erentat∈gw,r→x<br>r_2-r_1=(Ldy)/(dx)-0<br>implies(dy)/(dx)=(r_2-r_1)/L<br>implies(r_2-r_1)/(L)dx=(dyL)/(r_2-r_1) …(i)<br>(Q/t)=(k pi y^2 d theta )/(dx)<br>Now (Qdx)/t=(k pi y^2 d theta )/(dx)<br>implies(QLdy)/(t(r-2-r_1))=(k pi y^2 Delta theta )<br>[Fromequation(i)]
⇒dθ=QLdyt(r2−r1)kπy2
Intrgrating both side
⇒∫θ2θ1dθ=QLt(r2−r1)kπ∫r1r2(dy)/(y2)
⇒(θ2−θ1)=QLt(r2−r1)kπ×[−1y]r2r1
⇒(θ2−θ1)=QLt(r2−r1)kπ×[1r1−1r2]
⇒(θ2−θ1)=QLt(r2−r1)kπ(r2−r1)r2r1
⇒(Qt)=(kπ(r2r1)θ1−θ2L.
Topper's Solved these Questions
- HEAT TRANSFERBOOK - HC VERMA ENGLISHCHAPTER - HEAT TRANSFEREXERCISE - QUESTIONS FOR SHORT ANSWER
11 Videos
- HEAT TRANSFERBOOK - HC VERMA ENGLISHCHAPTER - HEAT TRANSFEREXERCISE - OBJECTIVE II
6 Videos
- HEAT AND TEMPERATUREBOOK - HC VERMA ENGLISHCHAPTER - HEAT AND TEMPERATUREEXERCISE - Objective 2
6 Videos
- INTRODUCTION TO PHYSICSBOOK - HC VERMA ENGLISHCHAPTER - INTRODUCTION TO PHYSICSEXERCISE - Question for short Answer
4 Videos
Similar Questions
A hole of radius r1 is made centrally in a uniform circular disc of thickness d and radius r2 . The inner surface (a cylinder of length d and radius r1) is maintained at a temperature θ1 and the outer surface (a cylinder of length d and radius r2) is maintained at a temperature θ2(θ1>θ2) .The thermal conductivity of the material of the disc is K. Calculate the heat flowing per unit time through the disc.
View SolutionA composite rod made of three rods of equal length and cross-section as shown in fig. The thermal conductivites of the materials of the rods are K/2, 5K and K respectively. The end A and end B are at constant tempertures. All heat entering the face A goes out of the end B there being no loss of heat from the sides of the bar. The effective thermal conductivity of the bar is

View SolutionA metal rod of cross sectional area 1.0cm2 is being heated at one end. At one time , the temperature gradient is 5.0∘Ccm−1 at cross section A and is 2.5∘Ccm−1 at cross section B. calculate the rate at which the temperature is increasing in the part AB of the rod. The heat capacity of the part AB=0.40J∘C−1 , thermal conductivity of the material of the rod. K=200Wm−1C−1 . Neglect any loss of heat to the atmosphere.
View SolutionTwo rods (one semi-circular and other straight) of same material and of same cross-sectional area are joined as shown in the figure. The point A and B are maintained at different temperature. Find the ratio of the heat transferred through a cross-section of a semi-circular rod to the heat transferred through a cross section of the straight rod in a given time.

View SolutionTwo identical square rods of metal are welded end to end as shown in figure (a). Assume that 10 cal of heat flows through thr rod in 2min. Now the rods are welded as shown in figure (b). The time it would take for 10 cal to flow through the rods now, is

View SolutionTwo identical square rods of metal are welded end to end as shown in figure (i), 20 calories of heat flows through it in 4 minutes. If the rods are welded as shown in figure (ii), the same amount of heat will flow through the rods in
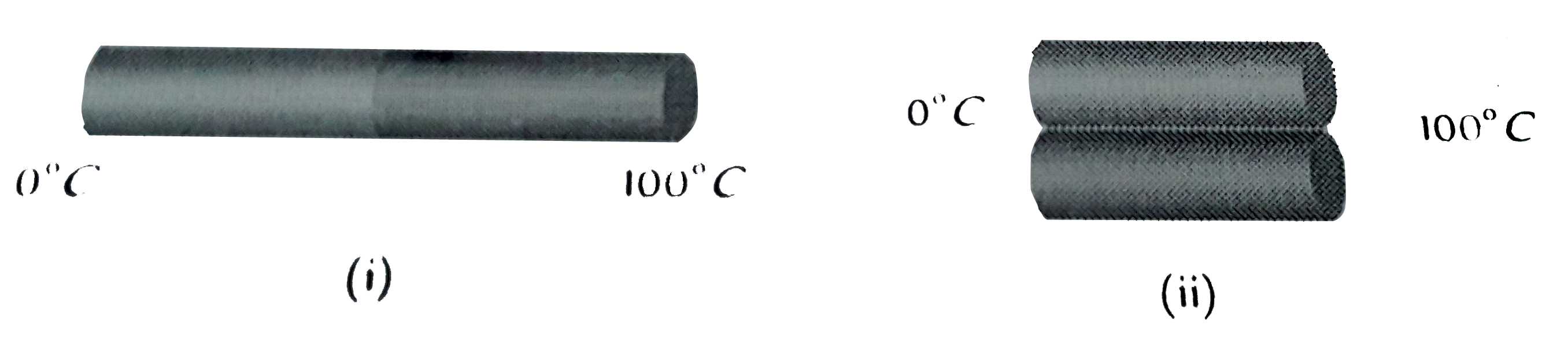
View SolutionTwo rods A and B of different materials are welded together as shown in figure. Their thermal conductivities are K1 and K2. The thermal conductivity of the composite rod will be

View SolutionThree rods each of same length and cross - section are joined in series. The thermal conductivity of the materials are K, 2K and 3K respectively. If one end is kept at 200∘C and the other at 100∘C. What would be the temperature of the junctions in the steady state? Assume that no heat is lost due to radiation from the sides of the rods.
View SolutionThe ratio of the areas of cross section of two rods of different materials is 1:2 and the ratio of ther themal conductivities of their mateirals is 4: 3. On keeping equal temperature difference between the ends of theserods, the rate of conduction of heat are equal. The ratio of the lengths of the rods is
View SolutionTwo different rods A and B are kept as shown in figure . The variation of temperature of different cross sections with distance is plotted in a graph shown in figure . The ration of thermal conductivities of A andB is -
_E01_027_Q01.png)
View Solution
