Two long ,thin,solid cylinders are identical in size, by they are made of different substances with two different thermal conductivities. The two cylinders are connected in series between a reservoir at temperature Thot and a reservoir at temperature Tcold.The temperature at the boundary between the two cylinders is Tb. One can conclude that:-
Tb is closer to Thot than it is to Tcold.
Tb is closer to Tcold than it is to Thot.
Tb is closer to the temp. of the reservoir that is in contact with the cylinder with the lower thermal conductivity.
Tb is closer to the temp. of the reservoir that is in contact with the cylinder with the higher thermal conductivity.
The correct Answer is:D
For same rate of heat transfer the body having higher conductivity will have lower temperature difference. If cylinder with higher conductivity is connected with hot reservoir first then the function temperature Tb, will be closer to hot reservoir temperature.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -03
10 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - ASSERTION-REASON
36 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -01
65 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
Two identical rods are made of different materials whose thermal conductivities are K1andK2. They are placed end to end between two heat reservoirs at temperatures θ1andθ2. The temperature of the junction of the rod is

View SolutionTwo identical long, solid cylinders are used to conduct heat from temp T1 to Temp T2. Originally the cylinders are connected in series and the rate of heat transfer is H. If the cylinders are connected in parallel then the rate of heat transer would be:
View Solution
Knowledge Check
Two cylinders P and Q have the same length and diameter and are made of different materials having thermal conductivities in the ratio 2:3. These two cyinders ar combined to make a cylinder. One end of P is kept at 100∘C and another end of Q at 0∘C. THe temperature at the interface of P and Q is
A30∘CB40∘CC50∘CD60∘CTwo bars of same length and same cross-sectional area but of different thermal conductivites K1 and K2 are joined end to end as shown in the figure. One end of the compound bar it is at temperature T1 and the opposite end at temperature T2 (whereT1>T2). The temperature of the junction is
 AK1T1+K2T2K1+K2BK1T2+K2T1K1+K2CK1(T1+T2)K1+K2DK2T1+T2K1
AK1T1+K2T2K1+K2BK1T2+K2T1K1+K2CK1(T1+T2)K1+K2DK2T1+T2K1Two walls of thickness d1andd2 and thermal conductivites K1andK2 are in contact. In the steady state, if the temperature at the outer surfaces are T1andT2 the temperature at the common wall is
AK1T1d2+K2T2d1K1d2+K2d1BK1T1+K2T2d2+d1C(K1d1+K2d2T1+T2)T1T2DK1T1d1+K2T2d2K1d1+K2d2
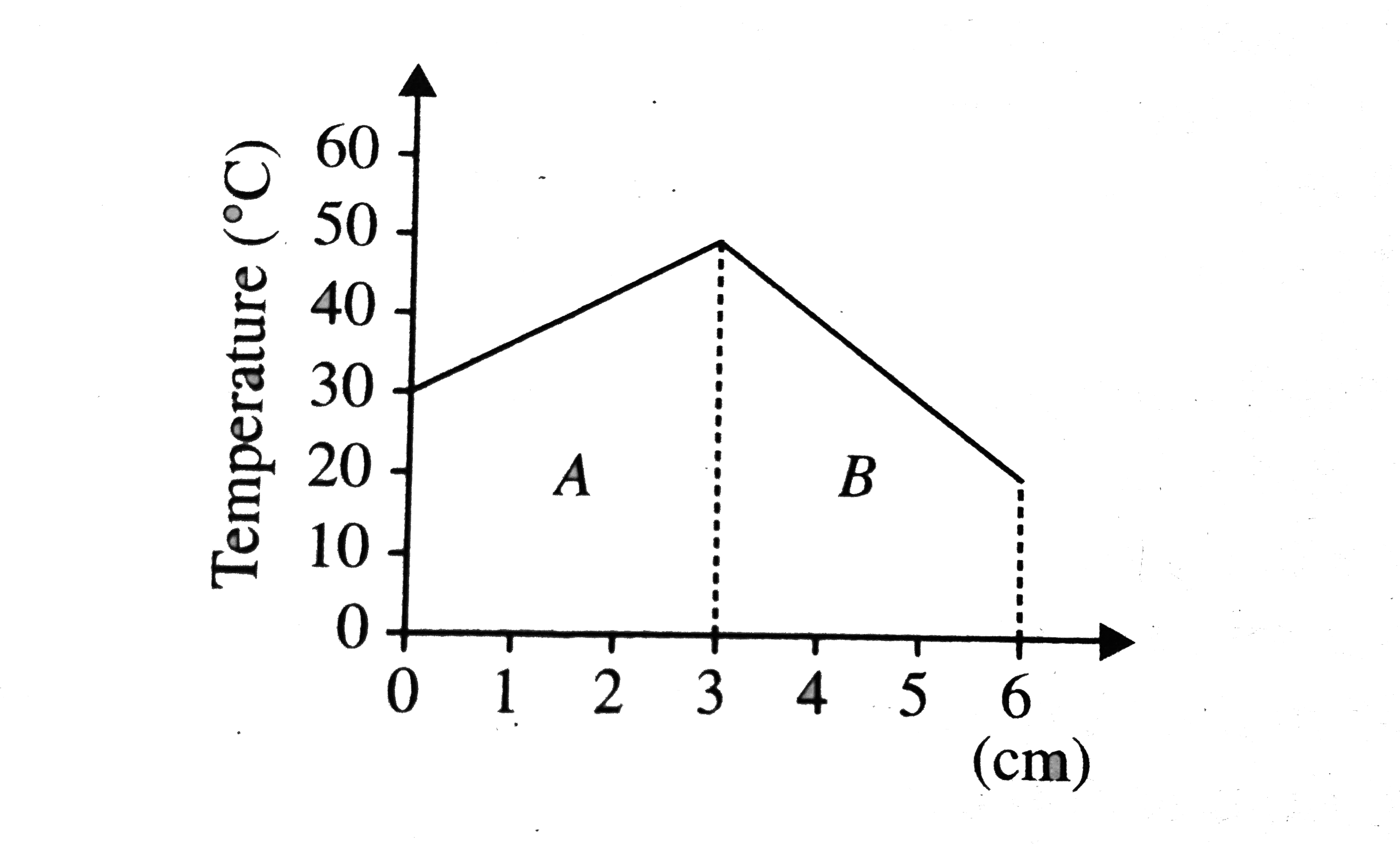
The temperature across two different slabs A and B are shown I the steady state (as shown Fig) The ratio of thermal conductivities of A and B is
View Solution
The temperature across two different slabs A and B are shown I the steady state (as shown Fig) The ratio of thermal conductivities of A and B is
View SolutionThe current - voltage graphs for a given metallic wire at two different temperatures T1andT2 are shown in the figure.
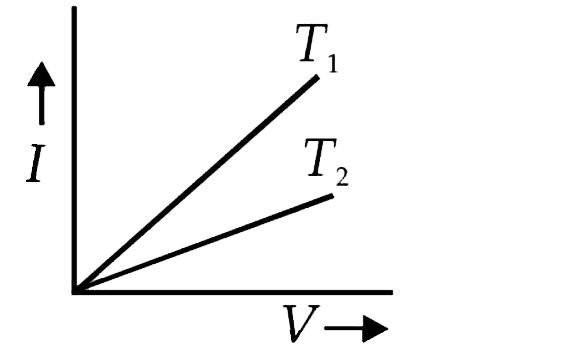
The temperature T2 is greater than T1.
View SolutionThe current - voltage graphs for a given metallic wire at two different temperatures T1andT2 are shown in the figure.

The temperature T2 is greater than T1.
View SolutionFour rods with different radii r and length l are used to connect two reservoirs of heat at different temperatures. Which one will conduct most heat ?
View Solution
