Two cylinders P and Q have the same length and diameter and are made of different materials having thermal conductivities in the ratio 2:3. These two cyinders ar combined to make a cylinder. One end of P is kept at 100∘C and another end of Q at 0∘C. THe temperature at the interface of P and Q is
30∘C
40∘C
50∘C
60∘C
The correct Answer is:B
To solve the problem, we need to find the temperature at the interface of two cylinders P and Q, which are made of different materials with thermal conductivities in the ratio of 2:3.
1. Identify the Given Data:
- Length of both cylinders (P and Q): L
- Diameter of both cylinders: same (not needed for calculations as it cancels out)
- Thermal conductivity of cylinder P: kP=2k
- Thermal conductivity of cylinder Q: kQ=3k
- Temperature at one end of P: TP=100∘C
- Temperature at one end of Q: TQ=0∘C
2. Set Up the Heat Transfer Equations:
Since both cylinders are in series, the heat transfer rate (Q/T) through both cylinders must be equal:
QT=kP⋅A⋅(TP−Tinterface)L=kQ⋅A⋅(Tinterface−TQ)L
3. Substituting the Known Values:
Substitute kP and kQ into the equation:
2k⋅A⋅(100−Tinterface)L=3k⋅A⋅(Tinterface−0)L
4. Cancel Common Terms:
Since k, A, and L are common on both sides, we can cancel them out:
2(100−Tinterface)=3Tinterface
5. Expand and Rearrange the Equation:
Expanding the left side:
200−2Tinterface=3Tinterface
Rearranging gives:
200=3Tinterface+2Tinterface⟹200=5Tinterface
6. Solve for the Temperature at the Interface:
Divide both sides by 5:
Tinterface=2005=40∘C
Final Answer:
The temperature at the interface of cylinders P and Q is 40∘C.
- Length of both cylinders (P and Q): L
- Diameter of both cylinders: same (not needed for calculations as it cancels out)
- Thermal conductivity of cylinder P: kP=2k
- Thermal conductivity of cylinder Q: kQ=3k
- Temperature at one end of P: TP=100∘C
- Temperature at one end of Q: TQ=0∘C
Since both cylinders are in series, the heat transfer rate (Q/T) through both cylinders must be equal:
QT=kP⋅A⋅(TP−Tinterface)L=kQ⋅A⋅(Tinterface−TQ)L
Substitute kP and kQ into the equation:
2k⋅A⋅(100−Tinterface)L=3k⋅A⋅(Tinterface−0)L
Since k, A, and L are common on both sides, we can cancel them out:
2(100−Tinterface)=3Tinterface
Expanding the left side:
200−2Tinterface=3Tinterface
Rearranging gives:
200=3Tinterface+2Tinterface⟹200=5Tinterface
Divide both sides by 5:
Tinterface=2005=40∘C
The temperature at the interface of cylinders P and Q is 40∘C.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - THERMAL RADIATION13videos
COMPETITION CARE UNIT
- BOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - OSCILLATIONS23videos
COMPETITION CARE UNIT
- BOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - INTERNAL ENERGY40videos
COMPETITION CARE UNIT
- BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 2 (FROM ROTATIONAL KINETIC ENERGY , WORK ,POWER)24videos
CIRCULAR MOTION
- BOOK - ICSECHAPTER - DIMENSIONSEXERCISE - SELECTED PROBLEMS (FROM CONVERSIONS OF ONE SYSTEMS OF UNITS INTO ANOTHER)9videos
DIMENSIONS
Similar Questions
A slab consists of two parallel layers of copper and brass of the same thichness and having thermal conductivities in the ratio 1:4 If the free face of brass is at 100∘C anf that of copper at 0∘C the temperature of interface is .
View SolutionTwo identical rods are made of different materials whose thermal conductivities are K1andK2. They are placed end to end between two heat reservoirs at temperatures θ1andθ2. The temperature of the junction of the rod is
View Solution
Knowledge Check
- Question 1 - Select One
The slab shown in the figure consists of two parallel layers of cooper anb brass of same thickness and having thermal conductivites in the ratio 4:1. IF the free face of the brass is at 100∘C and that of copper is at 0∘C, then the temperature of the interface will be
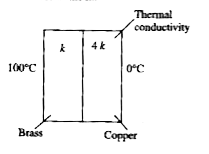A20∘CB30∘CC40∘CD25∘C - Question 2 - Select One
A wall has two layers A and B, each made of different materials. Both the layers have the same thickness. The thermal conductivity of the material of A is twice that of B. Under thermal equilibrium , the temperature differeence across the wall is 36∘C. The temperature difference across the layer A is
A6∘CB12∘CC18∘CD24∘C - Question 3 - Select One
A wall has two layers A and B, each made of different material. Both the layers have the same thickness. The thermal conductivity of the material of A is twice that of B . Under thermal equilibrium, the temperature difference across the wall is 36∘C. The temperature difference across the layer A is
A12.∘CB18.∘CC6.∘CD24.∘C
Same quantity of ice is filled in each of the two metal container P and Q having the same size, shape and will thickness but make of different materials. The containers are kept in identical surroundings, The ice in P melts completely in time t1, whereas in Q takes a time t2. The ratio of thermal conductivities of the materials of P and Q is:
View SolutionTwo metal wires P and Q of same length and material are stretched by same load. Yheir masses are in the ratio m1:m2. The ratio of elongation of wire P to that of Q is
View SolutionThree rods of the same dimensions have thermal conductivities 3k , 2k and k . They are arranged as shown, with their ends at 100∘C,50∘C and 0∘C. The temperature of their junction is :-
_E01_022_Q01.png)
View SolutionTwo rectangular blocks A and B of different metals have same length and same area of cross-section. They are kept in such a way that their cross-sectional area touch each other. The temperature at one end of A is 100∘C and B at the other end is 0∘C. If the ratio of their thermal conductivity is 1:3, then under steady state, the temperature of the junction in contact will be
View SolutionA wall has two layers A and B, each made of different material. Both the layers have the same thickness. The thermal conductivity of the material of A is twice that of B . Under thermal equilibrium, the temperature difference across the wall is 36∘C. The temperature difference across the layer A is
View Solution