Two walls of thickness d1andd2 and thermal conductivites K1andK2 are in contact. In the steady state, if the temperature at the outer surfaces are T1andT2 the temperature at the common wall is
K1T1d2+K2T2d1K1d2+K2d1
K1T1+K2T2d2+d1
(K1d1+K2d2T1+T2)T1T2
K1T1d1+K2T2d2K1d1+K2d2
The correct Answer is:A
To find the temperature at the common wall between two walls with given thicknesses and thermal conductivities, we can follow these steps:
1. Identify the Parameters:
- Let the thickness of the first wall be d1 and its thermal conductivity be K1.
- Let the thickness of the second wall be d2 and its thermal conductivity be K2.
- Let the outer temperatures be T1 (for the first wall) and T2 (for the second wall).
- We need to find the temperature at the common wall, denoted as T.
2. Understand the Heat Transfer:
- The heat transfer through both walls is in steady state, meaning the rate of heat flow (thermal current I) is constant across both walls.
- According to Fourier's law of thermal conduction, the heat transfer I can be expressed as:
I=K⋅A⋅(Thot−Tcold)L
- For the first wall:
I=K1⋅A⋅(T1−T)d1
- For the second wall:
I=K2⋅A⋅(T−T2)d2
3. Set the Heat Transfer Equations Equal:
- Since the heat transfer is the same through both walls, we set the two equations for I equal to each other:
K1⋅A⋅(T1−T)d1=K2⋅A⋅(T−T2)d2
- The area A cancels out from both sides.
4. Cross Multiply to Solve for T:
- Rearranging gives:
K1⋅d2⋅(T1−T)=K2⋅d1⋅(T−T2)
- Expanding both sides:
K1⋅d2⋅T1−K1⋅d2⋅T=K2⋅d1⋅T−K2⋅d1⋅T2
5. Combine Like Terms:
- Rearranging gives:
K1⋅d2⋅T1+K2⋅d1⋅T2=K1⋅d2⋅T+K2⋅d1⋅T
- Factor out T on the right side:
K1⋅d2⋅T1+K2⋅d1⋅T2=T(K1⋅d2+K2⋅d1)
6. Solve for T:
- Finally, solve for T:
T=K1⋅d2⋅T1+K2⋅d1⋅T2K1⋅d2+K2⋅d1
Final Answer:
The temperature at the common wall is given by:
T=K1⋅d2⋅T1+K2⋅d1⋅T2K1⋅d2+K2⋅d1
- Let the thickness of the first wall be d1 and its thermal conductivity be K1.
- Let the thickness of the second wall be d2 and its thermal conductivity be K2.
- Let the outer temperatures be T1 (for the first wall) and T2 (for the second wall).
- We need to find the temperature at the common wall, denoted as T.
- The heat transfer through both walls is in steady state, meaning the rate of heat flow (thermal current I) is constant across both walls.
- According to Fourier's law of thermal conduction, the heat transfer I can be expressed as:
I=K⋅A⋅(Thot−Tcold)L
- For the first wall:
I=K1⋅A⋅(T1−T)d1
- For the second wall:
I=K2⋅A⋅(T−T2)d2
- Since the heat transfer is the same through both walls, we set the two equations for I equal to each other:
K1⋅A⋅(T1−T)d1=K2⋅A⋅(T−T2)d2
- The area A cancels out from both sides.
- Rearranging gives:
K1⋅d2⋅(T1−T)=K2⋅d1⋅(T−T2)
- Expanding both sides:
K1⋅d2⋅T1−K1⋅d2⋅T=K2⋅d1⋅T−K2⋅d1⋅T2
- Rearranging gives:
K1⋅d2⋅T1+K2⋅d1⋅T2=K1⋅d2⋅T+K2⋅d1⋅T
- Factor out T on the right side:
K1⋅d2⋅T1+K2⋅d1⋅T2=T(K1⋅d2+K2⋅d1)
- Finally, solve for T:
T=K1⋅d2⋅T1+K2⋅d1⋅T2K1⋅d2+K2⋅d1
The temperature at the common wall is given by:
T=K1⋅d2⋅T1+K2⋅d1⋅T2K1⋅d2+K2⋅d1
Topper's Solved these Questions
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:THERMAL RADIATION
Explore 13 Videos
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:OSCILLATIONS
Explore 23 Videos
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:INTERNAL ENERGY
Explore 40 Videos
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 2 (FROM ROTATIONAL KINETIC ENERGY , WORK ,POWER)
Explore 24 Videos
- DIMENSIONSBook:ICSEChapter:DIMENSIONSExercise:SELECTED PROBLEMS (FROM CONVERSIONS OF ONE SYSTEMS OF UNITS INTO ANOTHER)
Explore 9 Videos
Similar Questions
Two plates eachb of area A, thickness L1andL2 thermal conductivities K1andK2 respectively are joined to form a single plate of thickness (L1+L2). If the temperatures of the free surfaces are T1andT2. Calculate.

(a) rate of flow of heat
(b) temperature of interface and
(c) equivalent thermal conductivity.
View SolutionTwo identical rods are made of different materials whose thermal conductivities are K1andK2. They are placed end to end between two heat reservoirs at temperatures θ1andθ2. The temperature of the junction of the rod is

View Solution
Knowledge Check
Two bars of same length and same cross-sectional area but of different thermal conductivites K1 and K2 are joined end to end as shown in the figure. One end of the compound bar it is at temperature T1 and the opposite end at temperature T2 (whereT1>T2). The temperature of the junction is
 AK1T1+K2T2K1+K2BK1T2+K2T1K1+K2CK1(T1+T2)K1+K2DK2T1+T2K1
AK1T1+K2T2K1+K2BK1T2+K2T1K1+K2CK1(T1+T2)K1+K2DK2T1+T2K1IF two metallic plates of equal thickness and thermal conductivities K1andK2 are put together face to face anda common plate is constructed, then the equivalent thermal conductivity of this plate will be
AK1K2K1+K2B2K1K2K1+K2C(K21_K22)3/2K1K2D(K21+K22)3/22K1K2The temperature of the two outer surfaces of a composite slab, consisting of two materials having coefficients of thermal conductivity K and 2K and thickness x and 4x respectively. Temperatures on the opposite faces of composite slab are T1andT2 where T2>T1, as shown in fig. what is the rate of flow of heat through the slab in a steady state?
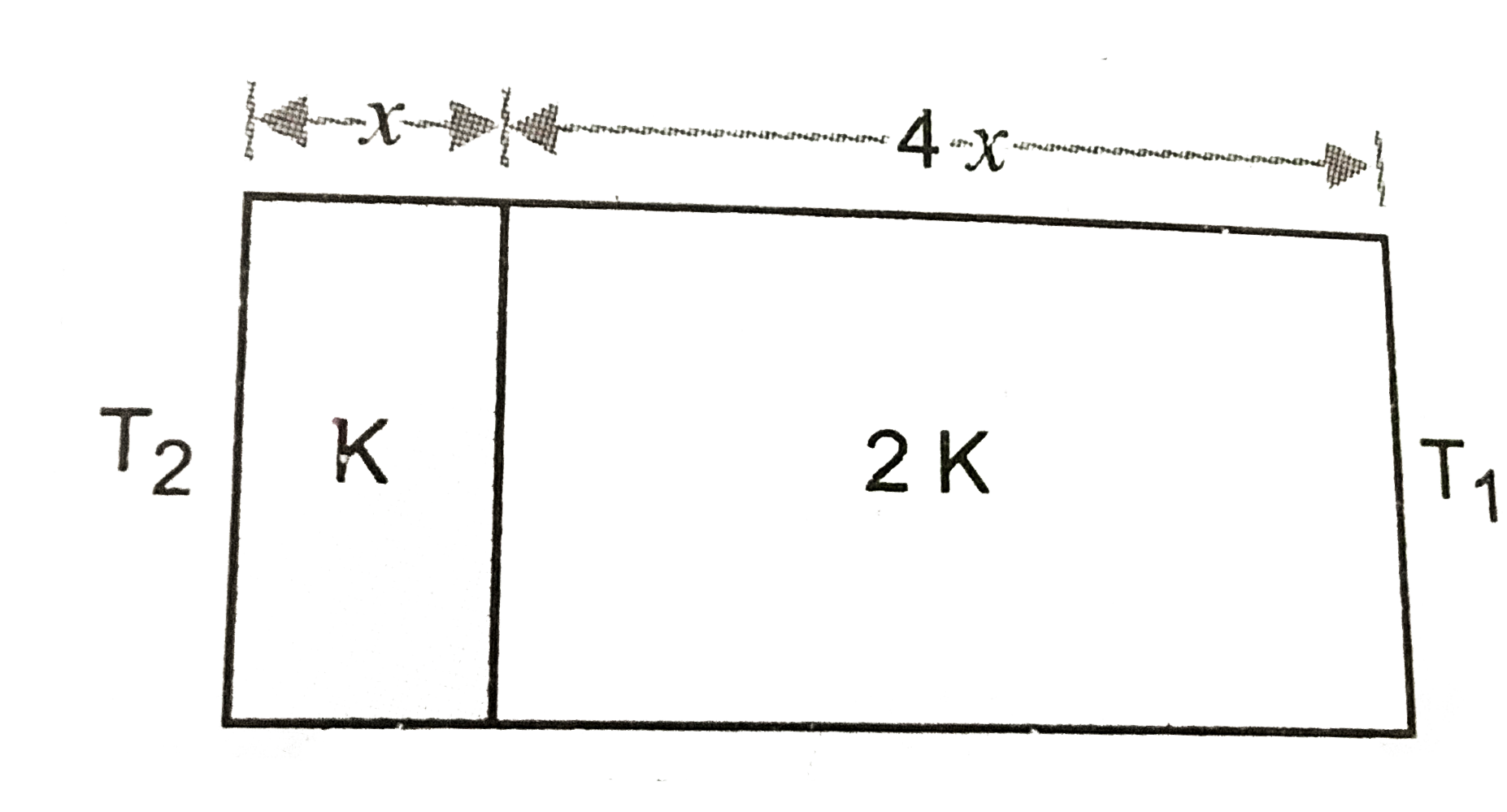 A1B12C23D13
A1B12C23D13
Two rods of length d1 and d2 and coefficients of thermal conductivites K1 and K2 are kept touching each other. Both have the same area of cross-section. The equivalent thermal conductivity.
View SolutionTwo bodies of masses m1 and m2 and specific heat capacities S1 and S2 are connected by a rod of length l, cross-section area A, thermal conductivity K and negligible heat capacity. The whole system is thermally insulated. At time t=0 , the temperature of the first body is T1 and the temperature of the second body is T2(T2>T1) . Find the temperature difference between the two bodies at time t.
View SolutionTwo bodies of masses m1 and m2 and specific heat capacities S1 and S2 are connected by a rod of length l, cross-section area A, thermal conductivity K and negligible heat capacity. The whole system is thermally insulated. At time t=0 , the temperature of the first body is T1 and the temperature of the second body is T2(T2>T1) . Find the temperature difference between the two bodies at time t.
View SolutionTwo plates of equal area are placed in contact with each other. The thickness of the plates are 2.0 cm and 3.0 cm respectively. The outer face of first plate is at −25∘C and that of second plate is at +25∘C. The conductivities of the plates are in the ratio 2:3. Calculate the temperature of the common surface of the plates.
View SolutionTwo conducting cylinders of equal length but different radii are connected in series between two heat baths kept at temperatures T1=300KandT2=100K, as shown in the figure. The radius of the bigger cylinder is twice that of the smaller one and the thermal conductivities of the materials of the smaller and the larger cylinders are K1andK2 respectively. If the temperature at the junction of the two cylinders in the steady state is 200 K, then K1/K2=__________.
View Solution