Two bodies of masses m1 and m2 and specific heat capacities S1 and S2 are connected by a rod of length l, cross-section area A, thermal conductivity K and negligible heat capacity. The whole system is thermally insulated. At time t=0 , the temperature of the first body is T1 and the temperature of the second body is T2(T2>T1) . Find the temperature difference between the two bodies at time t.
The correct Answer is:A, B, C, D
To solve the problem of finding the temperature difference between two bodies connected by a rod at any time t, we will follow these steps:
Step 1: Understand the System
We have two bodies with masses m1 and m2, specific heat capacities S1 and S2, and initial temperatures T1 and T2 (where T2>T1). They are connected by a rod with thermal conductivity K, length l, and cross-sectional area A. The system is thermally insulated.
Step 2: Heat Transfer Analysis
Since T2>T1, heat will flow from the second body (hotter) to the first body (cooler). We denote the temperatures of the two bodies at time t as T′1 and T′2.
Step 3: Heat Loss and Gain
The heat lost by the second body is given by:
Qlost=m2S2(T2−T′2)
The heat gained by the first body is:
Qgained=m1S1(T′1−T1)
Step 4: Rate of Heat Transfer
The rate of heat transfer through the rod can be expressed using Fourier's law:
dQdt=KAl(T′2−T′1)
Step 5: Setting Up the Equations
From the conservation of energy, we can equate the heat lost by the second body to the heat gained by the first body:
m2S2(T2−T′2)=m1S1(T′1−T1)
Step 6: Relating Temperature Changes
We can express the change in temperature in terms of the heat transfer rate:
1. For the second body:
dQdt=−m2S2dT′2dt
2. For the first body:
dQdt=m1S1dT′1dt
Step 7: Equating the Heat Transfer Rates
Equating the two expressions for dQdt:
−m2S2dT′2dt=KAl(T′2−T′1)
m1S1dT′1dt=KAl(T′2−T′1)
Step 8: Solving the Differential Equations
We can rearrange and integrate these equations to find T′1 and T′2 as functions of time t. The integration will yield an exponential decay function representing the temperature difference over time.
Step 9: Final Expression for Temperature Difference
After integrating and simplifying, we find that the temperature difference at any time t is given by:
ΔT(t)=(T2−T1)e−λt
where λ is a constant related to the thermal properties of the system.
Conclusion
The temperature difference between the two bodies at any time t can be expressed as:
ΔT(t)=(T2−T1)e−KAl⋅1m1S1+m2S2t
We have two bodies with masses m1 and m2, specific heat capacities S1 and S2, and initial temperatures T1 and T2 (where T2>T1). They are connected by a rod with thermal conductivity K, length l, and cross-sectional area A. The system is thermally insulated.
Since T2>T1, heat will flow from the second body (hotter) to the first body (cooler). We denote the temperatures of the two bodies at time t as T′1 and T′2.
The heat lost by the second body is given by:
Qlost=m2S2(T2−T′2)
The heat gained by the first body is:
Qgained=m1S1(T′1−T1)
The rate of heat transfer through the rod can be expressed using Fourier's law:
dQdt=KAl(T′2−T′1)
From the conservation of energy, we can equate the heat lost by the second body to the heat gained by the first body:
m2S2(T2−T′2)=m1S1(T′1−T1)
We can express the change in temperature in terms of the heat transfer rate:
1. For the second body:
dQdt=−m2S2dT′2dt
2. For the first body:
dQdt=m1S1dT′1dt
Equating the two expressions for dQdt:
−m2S2dT′2dt=KAl(T′2−T′1)
m1S1dT′1dt=KAl(T′2−T′1)
We can rearrange and integrate these equations to find T′1 and T′2 as functions of time t. The integration will yield an exponential decay function representing the temperature difference over time.
After integrating and simplifying, we find that the temperature difference at any time t is given by:
ΔT(t)=(T2−T1)e−λt
where λ is a constant related to the thermal properties of the system.
The temperature difference between the two bodies at any time t can be expressed as:
ΔT(t)=(T2−T1)e−KAl⋅1m1S1+m2S2t
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Level 2 More Than One Correct5videos
CALORIMETRY & HEAT TRANSFER
- BOOK - DC PANDEY ENGLISHCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise13videos
BASIC MATHEMATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery38videos
CALORIMETRY AND HEAT TRANSFER
Similar Questions
A rod of length l and cross-section area A has a variable thermal conductivity given by K = α T, where α is a positive constant and T is temperature in kelvin. Two ends of the rod are maintained at temperature T1 and T2 (T1>T2). Heat current flowing through the rod will be
View SolutionThree rods of equal length, area of cross section and thermal conductivity are connected as shown in the figure.
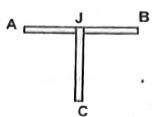
There is no heat loss through lateral surface of the rods and temperature of ends are TA=100∘C,TB=70∘C and TC=50∘C. Find the temperature of junction.View Solution
Knowledge Check
- Question 1 - Select One
Two chunks of metal with heat capacities C1 and C2, are interconnected by a rod length l and cross-sectional area S and fairly low heat conductivity K. The whole system is thermally insulated from the environment. At a moment t=0 the temperature difference betwene the two chunks of metal equals (ΔT)0. Assuming the heat capacity of the rod to be negligible, find the temperature difference between the chucks as a function of time.
AT0exp(−KA(C1+C2)tC1C2)BT0exp(−KA(C1+C2)C1C2)CT0exp(KA(C1+C2)tC1C2)DT0exp(KA(C1+C2)t2C1C2) - Question 2 - Select One
Two rods of length l1andl2 and coefficients of thermal conductivities k1andK2 are kept touching each other. Both have the same area of cross-section. The equivalent of thermal conductivity is
AK1+K2BK1l1+K2l2CK1l1+K2l2l1+l2Dl1+l2(l1/K1)+(l2/K2) - Question 3 - Select One
Two walls of thickness d1andd2 and thermal conductivites K1andK2 are in contact. In the steady state, if the temperature at the outer surfaces are T1andT2 the temperature at the common wall is
AK1T1d2+K2T2d1K1d2+K2d1BK1T1+K2T2d2+d1C(K1d1+K2d2T1+T2)T1T2DK1T1d1+K2T2d2K1d1+K2d2
A rod of length l and cross sectional area A has a variable conductivity given by K=αT, where α is a positive constant T is temperatures in Kelvin. Two ends of the rod are maintained at temperatures T1 and T2(T1>T2). Heat current flowing through the rod will be
View SolutionTwo bodies of specific heats C1andC2 having same heat capacities are combined to form a single composite body. What is the specific heat of the composite body?
View SolutionGibbs-Helmoholtz equation relates the free energy change to the enthalpy and entropy changes of the process as
(ΔG)PT=ΔH−TΔS
The magnitude of ΔH does not change much with the change in temperature but the energy factor TΔS changes appreciably. Thus, spontaneity of a process depends very much on temperature.
The dissolution of CaCl2.6H2O in a large volume of water is endothermic to the extent of 3.5kcalmol−1. For the reaction. CaCl2(s)+6H2O(l)→CaCl2.6H2O(s)ΔHis−23.2kcal. The heat of solution of anhydrous CaCI2 in large quantity of water will beView SolutionTwo bodies of specific heats s1ands2 having same heat capacities are combinated to form a single composite body. Find the specific heat of the composite body.
View SolutionTwo bars of same length and same cross-sectional area but of different thermal conductivites K1 and K2 are joined end to end as shown in the figure. One end of the compound bar it is at temperature T1 and the opposite end at temperature T2 (whereT1>T2). The temperature of the junction is
 View Solution
View Solution
