Two bars of same length and same cross-sectional area but of different thermal conductivites K1 and K2 are joined end to end as shown in the figure. One end of the compound bar it is at temperature T1 and the opposite end at temperature T2 (whereT1>T2). The temperature of the junction is

K1T1+K2T2K1+K2
K1T2+K2T1K1+K2
K1(T1+T2)K1+K2
K2T1+T2K1
The correct Answer is:A

Let L and A be length and area of cross-section of each bar respectively.
∴ Heat current through the bar 1 is
H1=K1A(T1−T0)L
Here T0 is junction temperature.
Heat current through the bar 2 is
H2=K2A(T0−T2)L
At steady state, H1=H2
∴K1A(T1−T0)L=K2A(T0−T2)L
K1(T1−T0)=K2(T0−T2)
K1T1−K1T0=K2T0−K2T2
K1T0+K2T0=K1T1+K2T2
T0(K1+K2)=K1T1+K2T2
T0=K1T1+K2T2(K1+K2)......(i)
Topper's Solved these Questions
- THERMAL PROPERTIES OF MATTERBook:NCERT FINGERTPS ENGLISHChapter:THERMAL PROPERTIES OF MATTERExercise:Higher Order
Explore 8 Videos
- THERMAL PROPERTIES OF MATTERBook:NCERT FINGERTPS ENGLISHChapter:THERMAL PROPERTIES OF MATTERExercise:Exampler Problems
Explore 8 Videos
- THERMAL PROPERTIES OF MATTERBook:NCERT FINGERTPS ENGLISHChapter:THERMAL PROPERTIES OF MATTERExercise:Change of State
Explore 13 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBook:NCERT FINGERTPS ENGLISHChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSExercise:NCERT Exemplar
Explore 8 Videos
- THERMODYNAMICSBook:NCERT FINGERTPS ENGLISHChapter:THERMODYNAMICSExercise:Assertion And Reason
Explore 15 Videos
Similar Questions
Two identical rods are made of different materials whose thermal conductivities are K1andK2. They are placed end to end between two heat reservoirs at temperatures θ1andθ2. The temperature of the junction of the rod is

View SolutionThree rods of equal length, area of cross section and thermal conductivity are connected as shown in the figure.

There is no heat loss through lateral surface of the rods and temperature of ends are TA=100∘C,TB=70∘C and TC=50∘C. Find the temperature of junction.
View Solution
Knowledge Check
Two walls of thickness d1andd2 and thermal conductivites K1andK2 are in contact. In the steady state, if the temperature at the outer surfaces are T1andT2 the temperature at the common wall is
AK1T1d2+K2T2d1K1d2+K2d1BK1T1+K2T2d2+d1C(K1d1+K2d2T1+T2)T1T2DK1T1d1+K2T2d2K1d1+K2d2
Three bars of equal lengths and equal areas of cross-section are connected in series. Their thermal conductivities are in the ratio of 2:4:3. If the open ends of the first and last bars are at temperatures 20∘Cand18∘C respectively in the steady state calculate the temperature of both the junctions.
View SolutionA rod of length l and cross-section area A has a variable thermal conductivity given by K = α T, where α is a positive constant and T is temperature in kelvin. Two ends of the rod are maintained at temperature T1 and T2 (T1>T2). Heat current flowing through the rod will be
View SolutionTwo bodies of masses m1 and m2 and specific heat capacities S1 and S2 are connected by a rod of length l, cross-section area A, thermal conductivity K and negligible heat capacity. The whole system is thermally insulated. At time t=0 , the temperature of the first body is T1 and the temperature of the second body is T2(T2>T1) . Find the temperature difference between the two bodies at time t.
View SolutionI-V graph for a metallie wire at two different tempearture, T1andT2 is as shown in the figure. Which of the two temperatures is lower and why ?
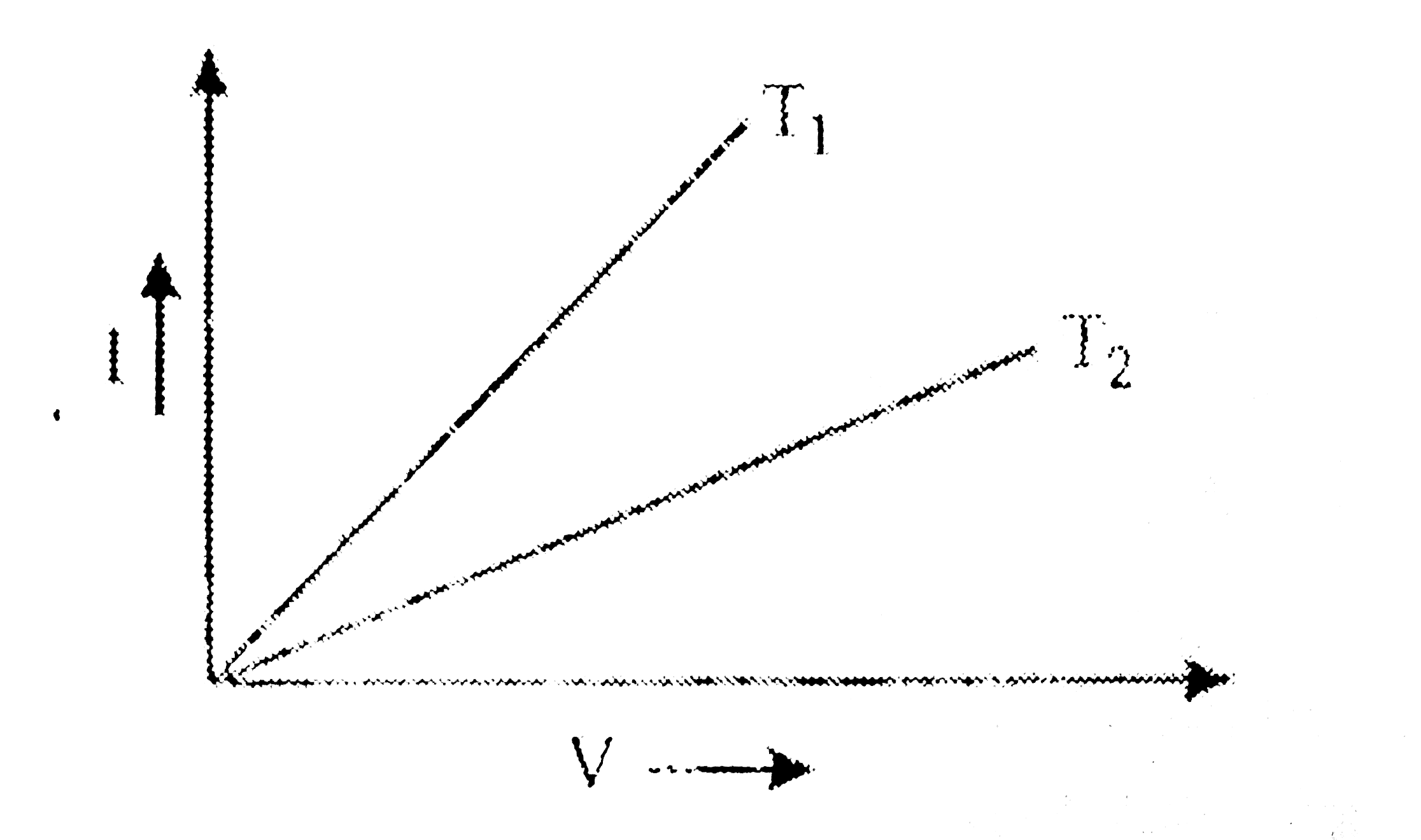
View SolutionTwo bodies of masses m1 and m2 and specific heat capacities S1 and S2 are connected by a rod of length l, cross-section area A, thermal conductivity K and negligible heat capacity. The whole system is thermally insulated. At time t=0 , the temperature of the first body is T1 and the temperature of the second body is T2(T2>T1) . Find the temperature difference between the two bodies at time t.
View SolutionTwo rods of length d1 and d2 and coefficients of thermal conductivites K1 and K2 are kept touching each other. Both have the same area of cross-section. The equivalent thermal conductivity.
View SolutionIf K1= Rate constant at temperature T1 and k2 rate constant at temperature T2 for a first order reaction, then which of the following relation is correct ?
View Solution

