Three bars of equal lengths and equal areas of cross-section are connected in series. Their thermal conductivities are in the ratio of 2:4:3. If the open ends of the first and last bars are at temperatures 20∘Cand18∘C respectively in the steady state calculate the temperature of both the junctions.
To solve the problem, we need to calculate the temperatures at the junctions of three bars connected in series, given their thermal conductivities and the temperatures at the ends.
1. Identify the Given Data:
- Let the thermal conductivities of the three bars be:
- k1=2k
- k2=4k
- k3=3k
- The lengths of the bars are equal, denoted as L.
- The cross-sectional area of the bars is equal, denoted as A.
- The temperatures at the ends are:
- T1=20∘C (at the end of the first bar)
- T3=18∘C (at the end of the third bar)
2. Calculate the Thermal Resistances:
- The thermal resistance R of a bar is given by the formula:
R=LkA
- Therefore, the resistances of the three bars are:
- R1=L2kA
- R2=L4kA
- R3=L3kA
3. Calculate the Total Resistance:
- The total resistance Rtotal in series is:
Rtotal=R1+R2+R3=L2kA+L4kA+L3kA
- To combine these fractions, find a common denominator (which is 12kA):
Rtotal=6L12kA+3L12kA+4L12kA=(6+3+4)L12kA=13L12kA
4. Calculate the Heat Current:
- The heat current Ih can be calculated using the temperature difference and total resistance:
Ih=T1−T3Rtotal=20−1813L12kA=2⋅12kA13L=24kA13L
5. Calculate the Temperature at Junction 1 (T2):
- The temperature drop across the first bar is given by:
T1−T2=Ih⋅R1=24kA13L⋅L2kA=2413⋅2=1213
- Therefore, the temperature at junction 1 is:
T2=T1−(T1−T2)=20−1213=260−1213=24813≈19.08∘C
6. Calculate the Temperature at Junction 2 (T2):
- The temperature drop across the second bar is:
T2−T3=Ih⋅R2=24kA13L⋅L4kA=2413⋅4=613
- Therefore, the temperature at junction 2 is:
T3=T2−(T2−T3)=T2−613=24813−613=24213≈18.62∘C
Final Results:
- Temperature at Junction 1 (T2): ≈19.08∘C
- Temperature at Junction 2 (T3): ≈18.62∘C
- Let the thermal conductivities of the three bars be:
- k1=2k
- k2=4k
- k3=3k
- The lengths of the bars are equal, denoted as L.
- The cross-sectional area of the bars is equal, denoted as A.
- The temperatures at the ends are:
- T1=20∘C (at the end of the first bar)
- T3=18∘C (at the end of the third bar)
- The thermal resistance R of a bar is given by the formula:
R=LkA
- Therefore, the resistances of the three bars are:
- R1=L2kA
- R2=L4kA
- R3=L3kA
- The total resistance Rtotal in series is:
Rtotal=R1+R2+R3=L2kA+L4kA+L3kA
- To combine these fractions, find a common denominator (which is 12kA):
Rtotal=6L12kA+3L12kA+4L12kA=(6+3+4)L12kA=13L12kA
- The heat current Ih can be calculated using the temperature difference and total resistance:
Ih=T1−T3Rtotal=20−1813L12kA=2⋅12kA13L=24kA13L
- The temperature drop across the first bar is given by:
T1−T2=Ih⋅R1=24kA13L⋅L2kA=2413⋅2=1213
- Therefore, the temperature at junction 1 is:
T2=T1−(T1−T2)=20−1213=260−1213=24813≈19.08∘C
- The temperature drop across the second bar is:
T2−T3=Ih⋅R2=24kA13L⋅L4kA=2413⋅4=613
- Therefore, the temperature at junction 2 is:
T3=T2−(T2−T3)=T2−613=24813−613=24213≈18.62∘C
- Temperature at Junction 1 (T2): ≈19.08∘C
- Temperature at Junction 2 (T3): ≈18.62∘C
Topper's Solved these Questions
- SAMPLE QUESTION PAPER-3 BOOK - ICSECHAPTER - SAMPLE QUESTION PAPER-3 EXERCISE - SECTION-C
9 Videos
- SAMPLE QUESTION PAPER-3 BOOK - ICSECHAPTER - SAMPLE QUESTION PAPER-3 EXERCISE - SECTION-D
6 Videos
- SAMPLE QUESTION PAPER-3 BOOK - ICSECHAPTER - SAMPLE QUESTION PAPER-3 EXERCISE - SECTION-D
6 Videos
- SAMPLE QUESTION PAPER-2 BOOK - ICSECHAPTER - SAMPLE QUESTION PAPER-2 EXERCISE - SECTION-D
10 Videos
- SELF ASSESSMENT PAPER 01BOOK - ICSECHAPTER - SELF ASSESSMENT PAPER 01EXERCISE - SECION- D (Answer the following )
6 Videos
Similar Questions
Three bars of equal lengths and equal area of cross-section are connected in series fig. their thermal conducitives are in the ratio 2:3:4. If at the steady state the open ends of the first and the last bars are at temperature 200∘C and 20∘C respectively, find the temperature of both the junctions.
 .
.
View SolutionThree rods A, B and C of the same length and same cross-sectional area are joined as shown. Their thermal conductivities are in the ratio 1:2:3/2. If the open ends of A and C are at 200∘C and 18∘C, respectively, then the temperature at the junction of A at steady state is
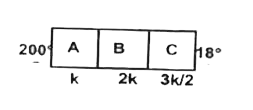
View Solution
Knowledge Check
Two bars of same length and same cross-sectional area but of different thermal conductivites K1 and K2 are joined end to end as shown in the figure. One end of the compound bar it is at temperature T1 and the opposite end at temperature T2 (whereT1>T2). The temperature of the junction is
 AK1T1+K2T2K1+K2BK1T2+K2T1K1+K2CK1(T1+T2)K1+K2DK2T1+T2K1
AK1T1+K2T2K1+K2BK1T2+K2T1K1+K2CK1(T1+T2)K1+K2DK2T1+T2K1
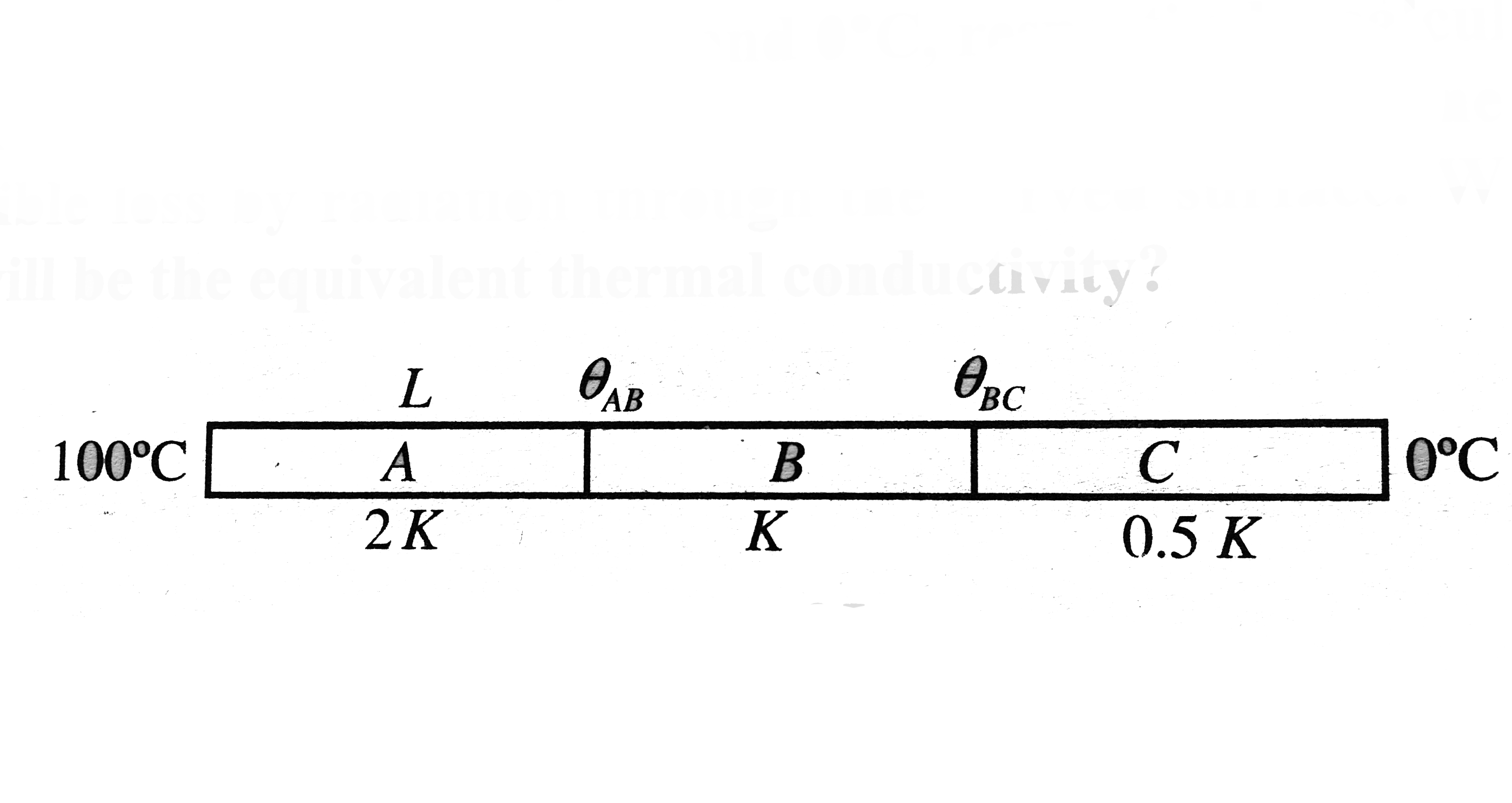
Three cylindrical rods A, B and C of equal lengths and equal diameters are joined in series as shown if Fig. Their thermal conductivities are 2K, K and 0.5K, respectively. In steady state, if the free ends of rods A and C are at 100∘C and 0∘C, respectively, calculate the temperature at the two junction points. Assume negligible loss by radiaiotn through the curved surface. What will be the equivalent thermal conductivity?
View SolutionTwo walls of thickness in the ratio 1:3 and thermal conductivities in the ratio 3:2 form a composite wall of a building. If the free surfaces of the wall be at temperatures 30∘C and 20∘C, respectively, what is the temperature of the interface?
View SolutionTwo ends of a conducting rod of varying cross-section are maintained at 200∘C and 0∘C respectively. In steady state:

View SolutionThree rods each of same length and cross - section are joined in series. The thermal conductivity of the materials are K, 2K and 3K respectively. If one end is kept at 200∘C and the other at 100∘C. What would be the temperature of the junctions in the steady state? Assume that no heat is lost due to radiation from the sides of the rods.
View SolutionTwo rods of similar area of cross section and length are joined as shown in the figure. The ratio of their thermal conductivity is 2:3. The free ends are maintained at 100∘C and 0∘C respectivley. THE temperature at junction in steady state is

View Solution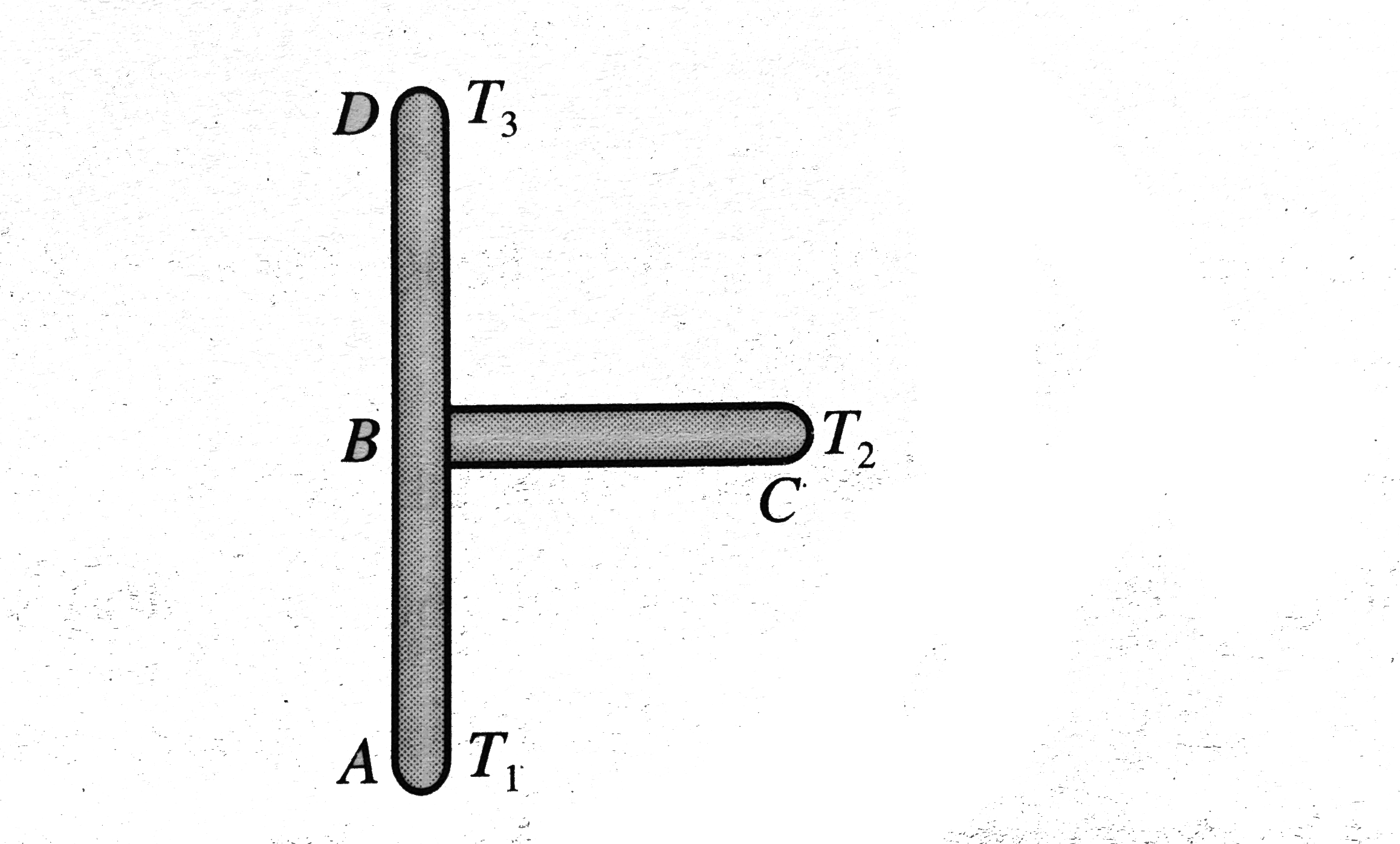
Three rods AB, BC and BD having thermal conductivities in the ratio 1:2:3 and lengths in the ratio 2:1:1 are joined as shown in Fig. The ends A, C and D are at temperature T1,T2 and T3 respectively Find the temperature of the junction B. Assume steady state.
View SolutionTwelve conducting rods from the sides of a uniform cube of side l. If in steady state, B and H ends of the cube are at 100∘C and 0∘C respectively. Find the temperature of the junction 'A' :-
_E01_117_Q01.png)
View Solution
