Three very large plates of same area are kept parrallel and close to each other. They are considered as ideal black surfaces and have high thermal conductivity. The first and third plates are maintained at temperatures 2T and 3T respectively. The temperature of the middle (i.e., second) plate under steady state condition is
(652)1/4T
(974)1/4T
(972)1/4T
(97)1/4T
The correct Answer is:C
To find the temperature of the middle plate (the second plate) under steady-state conditions, we can follow these steps:
Step 1: Understand the setup
We have three large parallel plates:
- Plate 1 is at temperature 2T
- Plate 2 (the middle plate) is at an unknown temperature T′
- Plate 3 is at temperature 3T
Step 2: Write the power absorbed by the middle plate
The power absorbed by the middle plate (Plate 2) comes from both Plate 1 and Plate 3. The power absorbed from each plate can be calculated using the Stefan-Boltzmann law:
Pabsorbed=P1+P3=σA(2T)4+σA(3T)4
Step 3: Write the power radiated by the middle plate
The power radiated by the middle plate (Plate 2) is given by:
Pradiated=2σA(T′)4
Step 4: Set up the equation for steady-state
At steady state, the power absorbed by Plate 2 equals the power radiated by Plate 2:
σA(2T)4+σA(3T)4=2σA(T′)4
Step 5: Simplify the equation
We can cancel σA from both sides of the equation:
(2T)4+(3T)4=2(T′)4
Step 6: Calculate (2T)4 and (3T)4
Calculating the powers:
(2T)4=16T4
(3T)4=81T4
Step 7: Substitute back into the equation
Substituting these values back into the equation gives:
16T4+81T4=2(T′)4
Step 8: Combine terms
Combining the terms on the left side:
97T4=2(T′)4
Step 9: Solve for (T′)4
Dividing both sides by 2:
(T′)4=972T4
Step 10: Take the fourth root
Taking the fourth root of both sides gives:
T′=(972)1/4T
Final Answer
Thus, the temperature of the middle plate (Plate 2) under steady-state conditions is:
T′=971/421/4T
We have three large parallel plates:
- Plate 1 is at temperature 2T
- Plate 2 (the middle plate) is at an unknown temperature T′
- Plate 3 is at temperature 3T
The power absorbed by the middle plate (Plate 2) comes from both Plate 1 and Plate 3. The power absorbed from each plate can be calculated using the Stefan-Boltzmann law:
The power radiated by the middle plate (Plate 2) is given by:
At steady state, the power absorbed by Plate 2 equals the power radiated by Plate 2:
We can cancel σA from both sides of the equation:
Calculating the powers:
(3T)4=81T4
Substituting these values back into the equation gives:
Combining the terms on the left side:
Dividing both sides by 2:
Taking the fourth root of both sides gives:
Thus, the temperature of the middle plate (Plate 2) under steady-state conditions is:
Topper's Solved these Questions
- THERMAL PROPERTIES OF MATTERBook:NCERT FINGERTPS ENGLISHChapter:THERMAL PROPERTIES OF MATTERExercise:Higher Order
Explore 8 Videos
- THERMAL PROPERTIES OF MATTERBook:NCERT FINGERTPS ENGLISHChapter:THERMAL PROPERTIES OF MATTERExercise:Exampler Problems
Explore 8 Videos
- THERMAL PROPERTIES OF MATTERBook:NCERT FINGERTPS ENGLISHChapter:THERMAL PROPERTIES OF MATTERExercise:Change of State
Explore 13 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBook:NCERT FINGERTPS ENGLISHChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSExercise:NCERT Exemplar
Explore 8 Videos
- THERMODYNAMICSBook:NCERT FINGERTPS ENGLISHChapter:THERMODYNAMICSExercise:Assertion And Reason
Explore 15 Videos
Similar Questions
Two plates of equal area are placed in contact with each other. The thickness of the plates are 2.0 cm and 3.0 cm respectively. The outer face of first plate is at −25∘C and that of second plate is at +25∘C. The conductivities of the plates are in the ratio 2:3. Calculate the temperature of the common surface of the plates.
View Solution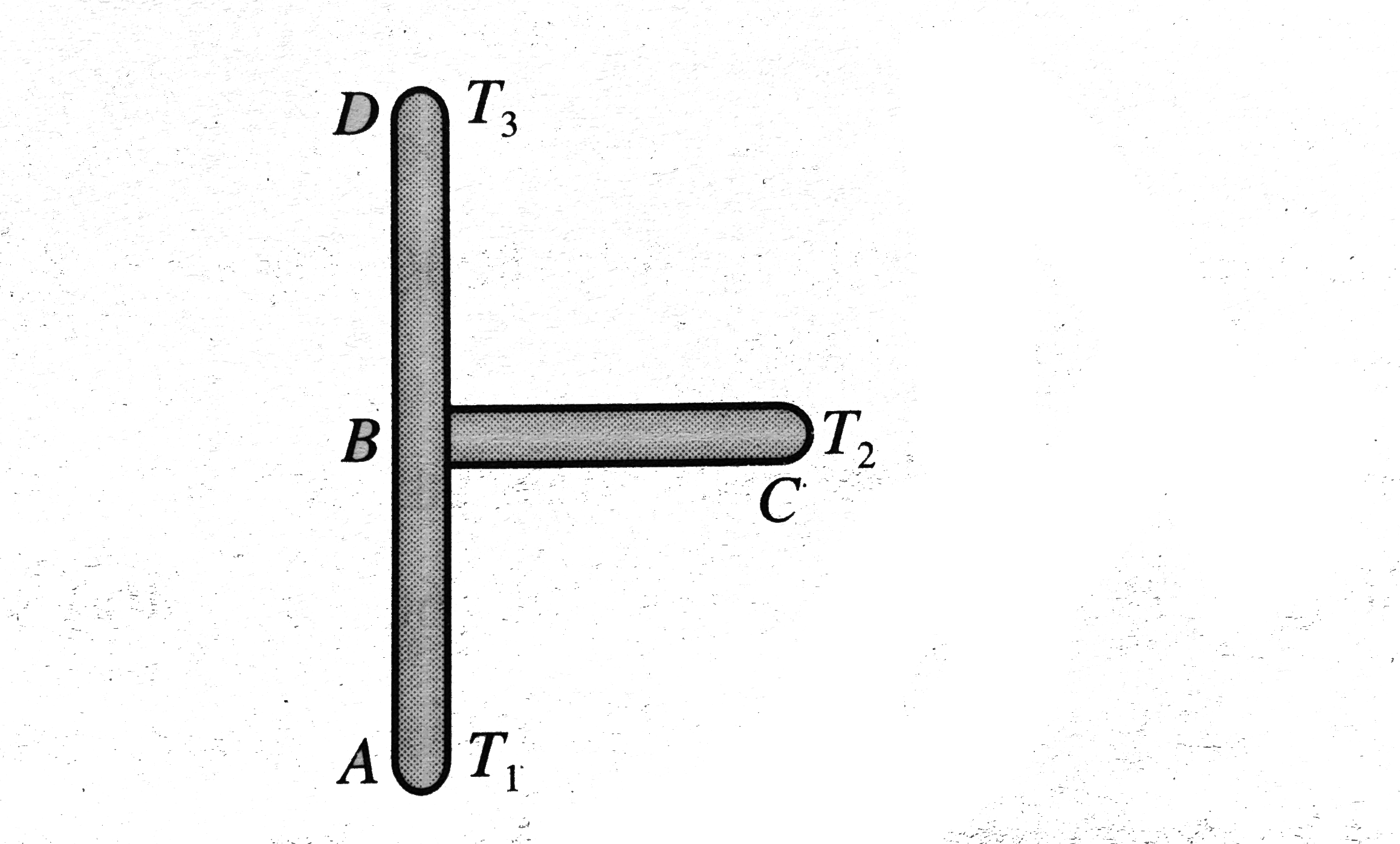
Three rods AB, BC and BD having thermal conductivities in the ratio 1:2:3 and lengths in the ratio 2:1:1 are joined as shown in Fig. The ends A, C and D are at temperature T1,T2 and T3 respectively Find the temperature of the junction B. Assume steady state.
View Solution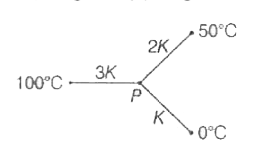
Three rods of the same dimension have thermal conductivity 3K , 2K and K. They are arranged as shown in the figure below
Then , the temperature of the junction in steady - state is
View SolutionAll the rods have same conductance 'K' and same area of cross section 'A'. If ends A and C are maintained at temperature 2T0 and T0 respectively then which of the following is/are correct?
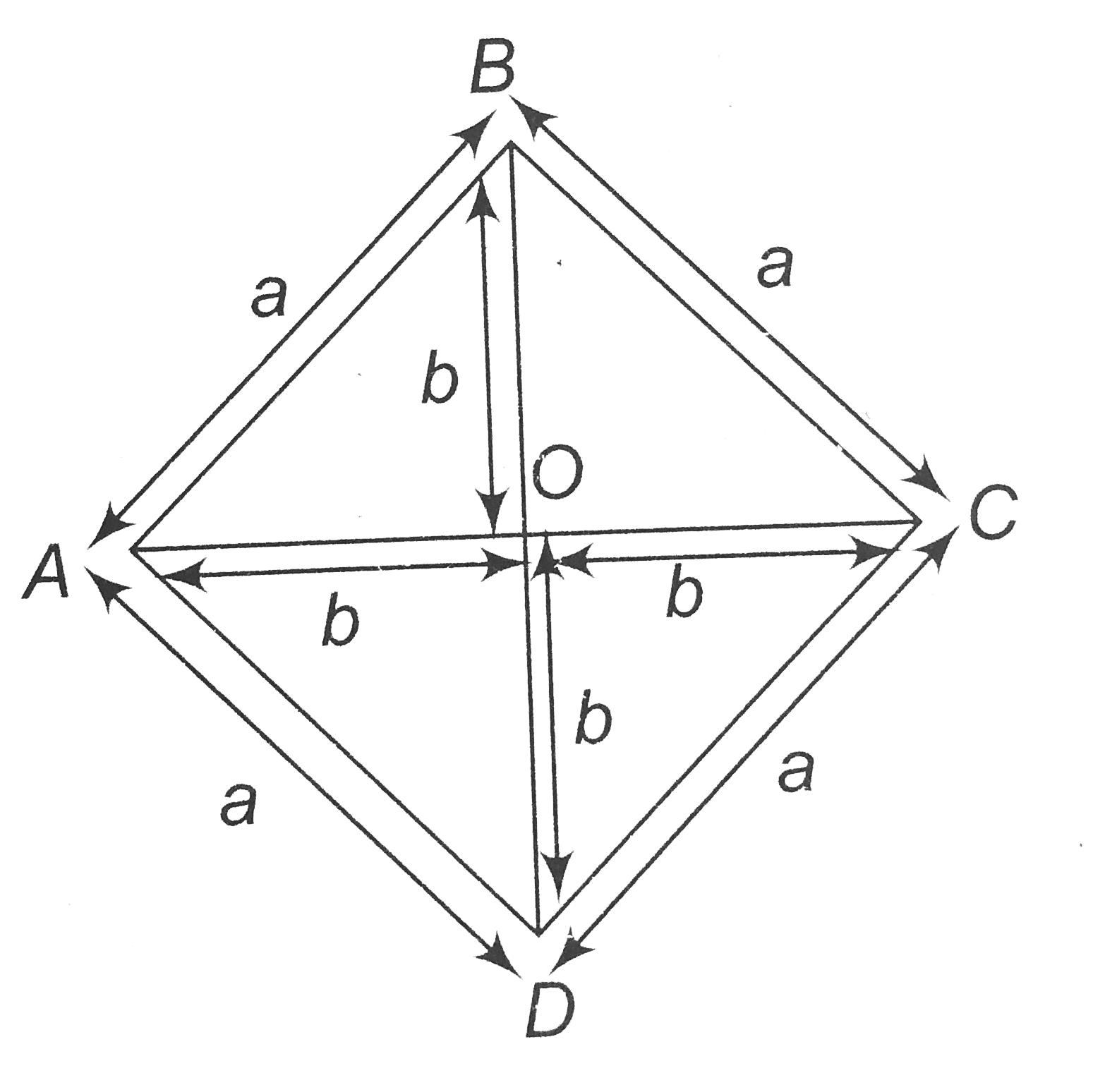
View Solution
Eleven identical rods are arranged as shown in Fig. Each rod has length l, cross sectional area A and thermal conductivity of material k. Ends A and F are maintained at temperatures T1 and T2(<T1), respectively. If lateral surface of each rod is thermally insulated, the rate of heat transfer (dQdt) in each rod is
View SolutionThree rods of same dimensions have thermal conductivity 3K,2K and K They are arranged as shown in Then the temperature of the junction in steady state is
 .
.
View Solution
Two ends of a rod of uniform cross sectional area are kept at temperature 3T0 and T0 as shown. Thermal conductivity of rod varies as k=αT, (where α is a constant and T is absolute temperature). In steady state, the temperature of the middle section of the rod is
View SolutionThree rods of identical area of cross-section and made from the same metal from the sides of an isosceles triangle. ABC, right angled at B. The points A and B are maintained at temperatures T and √2T RESPECTIVELY. In the steady state the temperature of the point C is TC.
Assuming that only heat conduction takes place , TCT is equal to
View SolutionThree rods of identical cross-sectional area and made from the same metal form the sides of an equilateral triangle ABC The points A and B are maintained at temperature √3T and T respectively In the steady state, the temperature of the point C is TC Assuming that only heat conduction takes place, the value of TC/T is equal to .
View SolutionThree rods A, B and C of the same length and same cross-sectional area are joined as shown. Their thermal conductivities are in the ratio 1:2:3/2. If the open ends of A and C are at 200∘C and 18∘C, respectively, then the temperature at the junction of A at steady state is
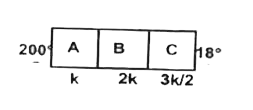
View Solution

