Three rods of identical area of cross-section and made from the same metal from the sides of an isosceles triangle. ABC, right angled at B. The points A and B are maintained at temperatures T and √2T RESPECTIVELY. In the steady state the temperature of the point C is TC.
Assuming that only heat conduction takes place , TCT is equal to
1√2+1
3√2+1
12(2√2−1)
1√3(√2−1)
The correct Answer is:B
To solve the problem, we need to analyze the heat conduction through the rods forming the isosceles right triangle ABC, where point A is at temperature T, point B is at temperature √2T, and we need to find the temperature at point C (denoted as TC) in terms of T.
1. Identify the Geometry and Temperatures:
- We have an isosceles right triangle ABC with right angle at B.
- Let the lengths of sides AB and BC be L.
- The length AC (hypotenuse) will be L√2.
- The temperatures are given as:
- TA=T (at point A)
- TB=√2T (at point B)
- TC=TC (at point C, which we need to find)
2. Thermal Resistance Calculation:
- The thermal resistance R for a rod is given by:
R=LkA
where k is the thermal conductivity and A is the cross-sectional area.
- For rod AB (length L), the thermal resistance RAB=LkA.
- For rod BC (length L), the thermal resistance RBC=LkA.
- For rod AC (length L√2), the thermal resistance RAC=L√2kA=√2R.
3. Apply the Steady State Condition:
- In steady state, the heat current through each rod must be equal:
IBC=IAC
- The heat current I can be expressed as:
I=Thot−TcoldR
- For rod BC:
IBC=√2T−TCR
- For rod AC:
IAC=TC−T√2R
4. Set the Heat Currents Equal:
- Equating the two expressions for heat current:
√2T−TCR=TC−T√2R
- Cancel R from both sides:
√2T−TC=TC−T√2
5. Clear the Fraction:
- Multiply through by √2 to eliminate the fraction:
2T−√2TC=TC−T
6. Rearrange the Equation:
- Rearranging gives:
2T+T=TC+√2TC
3T=TC(1+√2)
7. Solve for TC:
- Now, solve for TC:
TC=3T1+√2
8. Find the Ratio TCT:
- Finally, we find the ratio:
TCT=31+√2
Final Answer:
TCT=31+√2
- We have an isosceles right triangle ABC with right angle at B.
- Let the lengths of sides AB and BC be L.
- The length AC (hypotenuse) will be L√2.
- The temperatures are given as:
- TA=T (at point A)
- TB=√2T (at point B)
- TC=TC (at point C, which we need to find)
- The thermal resistance R for a rod is given by:
R=LkA
where k is the thermal conductivity and A is the cross-sectional area.
- For rod AB (length L), the thermal resistance RAB=LkA.
- For rod BC (length L), the thermal resistance RBC=LkA.
- For rod AC (length L√2), the thermal resistance RAC=L√2kA=√2R.
- In steady state, the heat current through each rod must be equal:
IBC=IAC
- The heat current I can be expressed as:
I=Thot−TcoldR
- For rod BC:
IBC=√2T−TCR
- For rod AC:
IAC=TC−T√2R
- Equating the two expressions for heat current:
√2T−TCR=TC−T√2R
- Cancel R from both sides:
√2T−TC=TC−T√2
- Multiply through by √2 to eliminate the fraction:
2T−√2TC=TC−T
- Rearranging gives:
2T+T=TC+√2TC
3T=TC(1+√2)
- Now, solve for TC:
TC=3T1+√2
- Finally, we find the ratio:
TCT=31+√2
TCT=31+√2
Topper's Solved these Questions
- CALORIMETRY AND HEAT TRANSFERBook:DC PANDEY ENGLISHChapter:CALORIMETRY AND HEAT TRANSFERExercise:Assertion and reason
Explore 17 Videos
- CALORIMETRY AND HEAT TRANSFERBook:DC PANDEY ENGLISHChapter:CALORIMETRY AND HEAT TRANSFERExercise:Match the columns
Explore 4 Videos
- CALORIMETRY AND HEAT TRANSFERBook:DC PANDEY ENGLISHChapter:CALORIMETRY AND HEAT TRANSFERExercise:Check points 16.4
Explore 29 Videos
- CALORIMETRY & HEAT TRANSFERBook:DC PANDEY ENGLISHChapter:CALORIMETRY & HEAT TRANSFERExercise:Level 2 Subjective
Explore 14 Videos
- CENTRE OF MASSBook:DC PANDEY ENGLISHChapter:CENTRE OF MASSExercise:Medical entrances gallery
Explore 27 Videos
Similar Questions
Three rods of identical cross-sectional area and made from the same metal form the sides of an equilateral triangle ABC The points A and B are maintained at temperature √3T and T respectively In the steady state, the temperature of the point C is TC Assuming that only heat conduction takes place, the value of TC/T is equal to .
View SolutionThree rods of identical cross-sectional area and made from the same metal form the sides of an isosceles triangle ABC right angled at B as shown in the figure. The points A and B are maintained at temperature T and (√2)T respectively in the steady state. Assuming that only heat conduction takes place, temperature of point C will be

View Solution
Knowledge Check
Three very large plates of same area are kept parrallel and close to each other. They are considered as ideal black surfaces and have high thermal conductivity. The first and third plates are maintained at temperatures 2T and 3T respectively. The temperature of the middle (i.e., second) plate under steady state condition is
A(652)1/4TB(974)1/4TC(972)1/4TD(97)1/4T
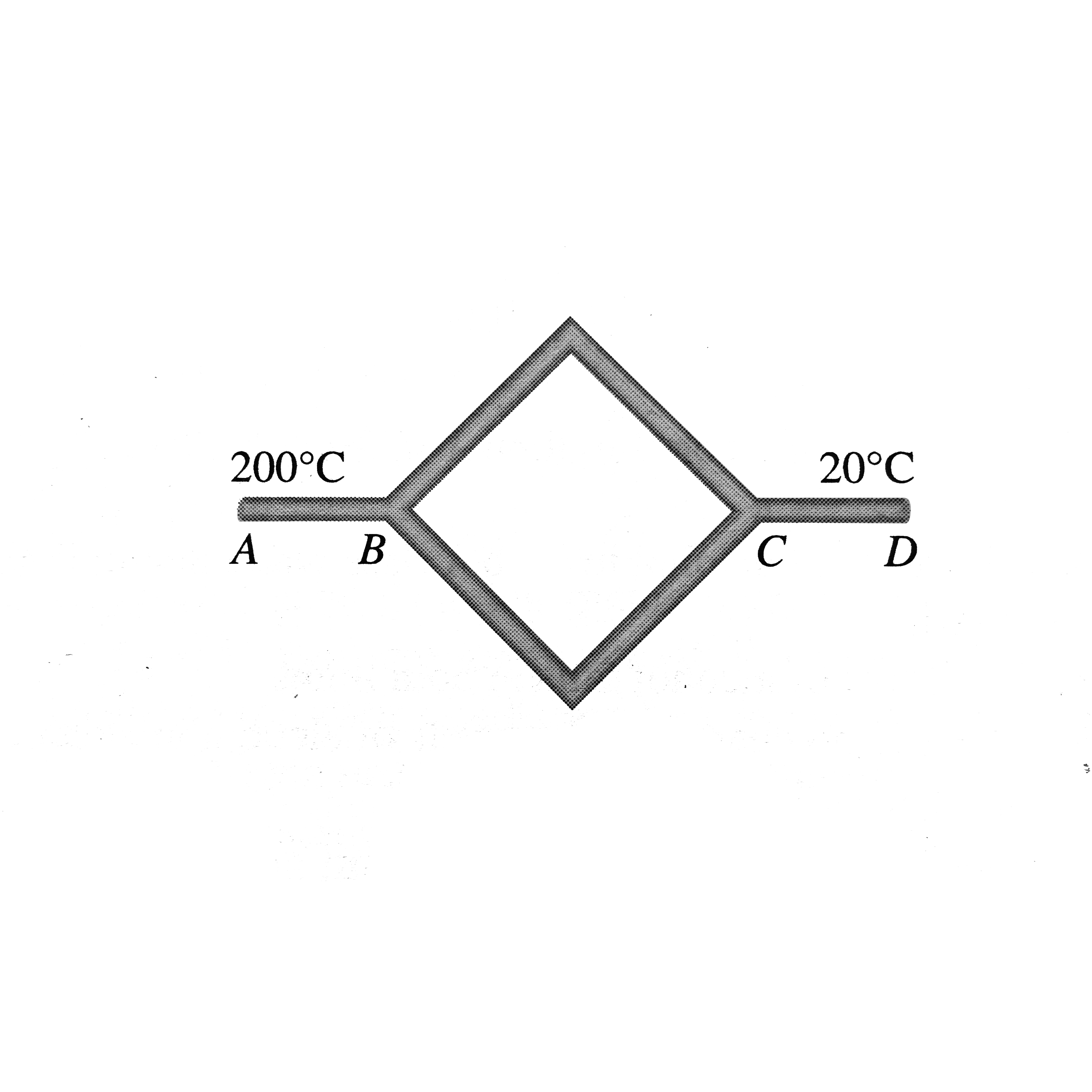
Six identical cunducting rods are joined as shown in Fig. Points A and D are maintained at temperatures 200∘C and 20∘C respectively. The temperature of junction B will be
View Solution
Six identical cunducting rods are joined as shown in Fig. Points A and D are maintained at temperatures 200∘C and 20∘C respectively. The temperature of junction B will be
View Solution
Six identical cunducting rods are joined as shown in Fig. Points A and D are maintained at temperatures 200∘C and 20∘C respectively. The temperature of junction B will be
View SolutionA metal rod of length 2 m has cross sectional areas 2 A and A as shown in figure. The ends are maintained at temperatures 100° C and 70° C . The temperature at middle point C is

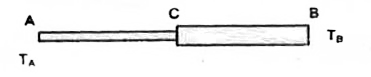
View SolutionTwo rods of same length and same material having area of cross section A and 4A respectively are joined as shown in the figure. If TA and TB are temperatures of free ends in steady state. The temperature of junction point C is (Assume no heat loss wil take place through lateral surface)
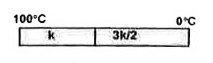
View SolutionTwo rods of similar area of cross section and length are joined as shown in the figure. The ratio of their thermal conductivity is 2:3. The free ends are maintained at 100∘C and 0∘C respectivley. THE temperature at junction in steady state is
View SolutionThree rods of equal length, area of cross section and thermal conductivity are connected as shown in the figure.
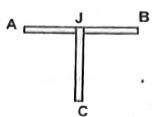
There is no heat loss through lateral surface of the rods and temperature of ends are TA=100∘C,TB=70∘C and TC=50∘C. Find the temperature of junction.
View Solution

