Two rods of equal length and diameter have thermal conductivite 3 and 4 units respectively. If they are joined in series, the thermal conductivity of the combination in the given units would be
3.43
4.43
5.43
2.43
The correct Answer is:A
To find the equivalent thermal conductivity of two rods joined in series, we can follow these steps:
Step 1: Understand the Given Information
We have two rods with the following properties:
- Length of both rods (L1 and L2) = L (equal for both)
- Diameter of both rods = same (implying equal cross-sectional area)
- Thermal conductivity of the first rod (k1) = 3 units
- Thermal conductivity of the second rod (k2) = 4 units
Step 2: Calculate the Thermal Resistance of Each Rod
The thermal resistance (R) of a rod can be calculated using the formula:
R=Lk⋅A
where:
- L = length of the rod
- k = thermal conductivity
- A = cross-sectional area
For the first rod (R1):
R1=Lk1⋅A=L3⋅A
For the second rod (R2):
R2=Lk2⋅A=L4⋅A
Step 3: Find the Total Thermal Resistance
When two resistances are in series, the total resistance (R_equivalent) is the sum of the individual resistances:
Requivalent=R1+R2=L3A+L4A
To add these fractions, find a common denominator (which is 12A):
Requivalent=4L12A+3L12A=7L12A
Step 4: Relate Total Resistance to Equivalent Thermal Conductivity
The equivalent thermal resistance can also be expressed in terms of the equivalent thermal conductivity (k_equivalent):
Requivalent=Lkequivalent⋅A
Setting the two expressions for Requivalent equal to each other:
Lkequivalent⋅A=7L12A
Step 5: Solve for k_equivalent
Cancel L and A from both sides:
1kequivalent=712
Taking the reciprocal gives:
kequivalent=127
Step 6: Calculate the Numerical Value
Now, calculate the numerical value:
kequivalent=127≈1.714 units
Conclusion
The equivalent thermal conductivity of the combination of the two rods joined in series is approximately 1.714 units.
---
We have two rods with the following properties:
- Length of both rods (L1 and L2) = L (equal for both)
- Diameter of both rods = same (implying equal cross-sectional area)
- Thermal conductivity of the first rod (k1) = 3 units
- Thermal conductivity of the second rod (k2) = 4 units
The thermal resistance (R) of a rod can be calculated using the formula:
R=Lk⋅A
where:
- L = length of the rod
- k = thermal conductivity
- A = cross-sectional area
R1=Lk1⋅A=L3⋅A
R2=Lk2⋅A=L4⋅A
When two resistances are in series, the total resistance (R_equivalent) is the sum of the individual resistances:
Requivalent=R1+R2=L3A+L4A
Requivalent=4L12A+3L12A=7L12A
The equivalent thermal resistance can also be expressed in terms of the equivalent thermal conductivity (k_equivalent):
Requivalent=Lkequivalent⋅A
Lkequivalent⋅A=7L12A
Cancel L and A from both sides:
1kequivalent=712
kequivalent=127
Now, calculate the numerical value:
kequivalent=127≈1.714 units
The equivalent thermal conductivity of the combination of the two rods joined in series is approximately 1.714 units.
Topper's Solved these Questions
- THERMAL PROPERTIES OF MATTERBook:NCERT FINGERTPS ENGLISHChapter:THERMAL PROPERTIES OF MATTERExercise:Higher Order
Explore 8 Videos
- THERMAL PROPERTIES OF MATTERBook:NCERT FINGERTPS ENGLISHChapter:THERMAL PROPERTIES OF MATTERExercise:Exampler Problems
Explore 8 Videos
- THERMAL PROPERTIES OF MATTERBook:NCERT FINGERTPS ENGLISHChapter:THERMAL PROPERTIES OF MATTERExercise:Change of State
Explore 13 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBook:NCERT FINGERTPS ENGLISHChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSExercise:NCERT Exemplar
Explore 8 Videos
- THERMODYNAMICSBook:NCERT FINGERTPS ENGLISHChapter:THERMODYNAMICSExercise:Assertion And Reason
Explore 15 Videos
Similar Questions

Statement I: Two solid cylindrical rods of identical size and different thermal conductivity K1 and K2 are connected in series. Then the equivalent thermal conductivity of two rods system is less than that value of thermal conductivity of either rod.
Statement II: For two cylindrical rods of identical size and different thermal conductivity K1 and K2 connected in series, the equivalent thermal conductivity K is given by 2K=1K1+1K2
View Solution
Statement I: Two solid cylindrical rods of identical size and different thermal conductivity K1 and K2 are connected in series. Then the equivalent thermal conductivity of two rods system is less than that value of thermal conductivity of either rod.
Statement II: For two cylindrical rods of identical size and different thermal conductivity K1 and K2 connected in series, the equivalent thermal conductivity K is given by 2K=1K1+1K2
View Solution
Knowledge Check
Consider a compound slab consisting of two different material having equal thickness and thermal conductivities K and 2K respectively. The equivalent thermal conductivity of the slab is
A23KB√2KC3KD43K
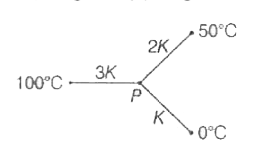
Three rods of the same dimension have thermal conductivity 3K , 2K and K. They are arranged as shown in the figure below
Then , the temperature of the junction in steady - state is
View SolutionConsider a compound slab consisting of two different material having equal thickness and thermal conductivities K and 2K respectively. The equivalent thermal conductivity of the slab is
View SolutionTwo conducting wires of the same material and of equal length and equal diameters are first connected in series and then in parallel in an electric circuit. The ratio of the heat produced in series and parallel combinations would be :
View SolutionTwo rods P and Q of equal lengths have thermal conductivities K1andK2 and cross-sectional areas A1andA2 respectively. If the temperature difference across the ends of each rod is the same, then the condition for which the rate of flow of heat through each of them will be equal, is
View SolutionThree rods of same dimensions have thermal conductivity 3K,2K and K They are arranged as shown in Then the temperature of the junction in steady state is
 .
.
View SolutionThree rods of same dimension are joined in series having thermal conductivity k1 , k2 and k3. The equivalent thermal conductivity is
View SolutionTwo identical plates with thermal conductivities K and 3K are joined together to form a single plate of double thickness. The equivalent thermal conductivity of one composite plate so formed for the flow of heat through its thickness is.
View Solution

