Three rods of copper, brass and steel are welded together to form a Y -shaped structure. The cross-sectional area of each rod is 4cm2. The end of copper rod is maintained at 100∘C and the ends of the brass and steel rods at 80∘C and 60∘C respectively. Assume that there is no loss of heat from the surfaces of the rods. The lengths of rods are : copper 46 cm, brass 13 cm and steel 12 cm.
(a) What is the temperature of the junction point?
(b) What is the heat current in the copper rod?
K(copper) = 0.92, K (steel) = 0.12 and K(brass) = 0.26 cal/cm−s∘C .
The correct Answer is:A, B, C, D
To solve the problem step by step, we will first determine the temperature of the junction point (T) and then calculate the heat current in the copper rod.
Given Data:
- Length of copper rod (L_c) = 46 cm
- Length of brass rod (L_b) = 13 cm
- Length of steel rod (L_s) = 12 cm
- Temperature at the end of copper rod (T_c) = 100°C
- Temperature at the end of brass rod (T_b) = 80°C
- Temperature at the end of steel rod (T_s) = 60°C
- Cross-sectional area (A) = 4 cm²
- Thermal conductivity:
- K_c (copper) = 0.92 cal/cm·s·°C
- K_b (brass) = 0.26 cal/cm·s·°C
- K_s (steel) = 0.12 cal/cm·s·°C
(a) Finding the Temperature of the Junction Point (T)
1. Set up the heat flow equations:
The heat flow (Q/t) through each rod can be expressed using Fourier's law of heat conduction:
Qt=K⋅A⋅(Thot−Tcold)L
For copper:
Qt=Kc⋅A⋅(Tc−T)Lc=0.92⋅4⋅(100−T)46
For brass:
Qt=Kb⋅A⋅(T−Tb)Lb=0.26⋅4⋅(T−80)13
For steel:
Qt=Ks⋅A⋅(T−Ts)Ls=0.12⋅4⋅(T−60)12
2. Equate the heat currents:
Since there is no heat loss, the heat current through copper and brass must equal the heat current through steel:
0.92⋅4⋅(100−T)46+0.26⋅4⋅(T−80)13=0.12⋅4⋅(T−60)12
3. Simplify the equation:
Cancel out the common factor of 4:
0.92(100−T)46+0.26(T−80)13=0.12(T−60)12
4. Multiply through by 46 to eliminate the denominator:
0.92(100−T)+0.26⋅3.54(T−80)=0.12⋅3.83(T−60)
(Note: 46/13 = 3.54 and 46/12 = 3.83)
5. Distribute and combine like terms:
92−0.92T+0.9264T−20.8=0.4596T−7.056
Combine all T terms and constants:
92−20.8+7.056=0.4596T+0.92T−0.9264T
78.256=0.4132T
6. Solve for T:
T=78.2560.4132≈189.3°C
(b) Finding the Heat Current in the Copper Rod
1. Use the heat flow equation for copper:
Qt=Kc⋅A⋅(Tc−T)Lc
Substitute the values:
Qt=0.92⋅4⋅(100−84)46
2. Calculate:
Qt=0.92⋅4⋅1646
Qt=58.7246≈1.28 cal/s
Final Answers:
(a) The temperature of the junction point is approximately 84°C.
(b) The heat current in the copper rod is approximately 1.28 cal/s.
- Length of copper rod (L_c) = 46 cm
- Length of brass rod (L_b) = 13 cm
- Length of steel rod (L_s) = 12 cm
- Temperature at the end of copper rod (T_c) = 100°C
- Temperature at the end of brass rod (T_b) = 80°C
- Temperature at the end of steel rod (T_s) = 60°C
- Cross-sectional area (A) = 4 cm²
- Thermal conductivity:
- K_c (copper) = 0.92 cal/cm·s·°C
- K_b (brass) = 0.26 cal/cm·s·°C
- K_s (steel) = 0.12 cal/cm·s·°C
The heat flow (Q/t) through each rod can be expressed using Fourier's law of heat conduction:
Qt=K⋅A⋅(Thot−Tcold)L
For copper:
Qt=Kc⋅A⋅(Tc−T)Lc=0.92⋅4⋅(100−T)46
For brass:
Qt=Kb⋅A⋅(T−Tb)Lb=0.26⋅4⋅(T−80)13
For steel:
Qt=Ks⋅A⋅(T−Ts)Ls=0.12⋅4⋅(T−60)12
Since there is no heat loss, the heat current through copper and brass must equal the heat current through steel:
0.92⋅4⋅(100−T)46+0.26⋅4⋅(T−80)13=0.12⋅4⋅(T−60)12
Cancel out the common factor of 4:
0.92(100−T)46+0.26(T−80)13=0.12(T−60)12
0.92(100−T)+0.26⋅3.54(T−80)=0.12⋅3.83(T−60)
(Note: 46/13 = 3.54 and 46/12 = 3.83)
92−0.92T+0.9264T−20.8=0.4596T−7.056
Combine all T terms and constants:
92−20.8+7.056=0.4596T+0.92T−0.9264T
78.256=0.4132T
T=78.2560.4132≈189.3°C
Qt=Kc⋅A⋅(Tc−T)Lc
Substitute the values:
Qt=0.92⋅4⋅(100−84)46
Qt=0.92⋅4⋅1646
Qt=58.7246≈1.28 cal/s
(a) The temperature of the junction point is approximately 84°C.
(b) The heat current in the copper rod is approximately 1.28 cal/s.
Topper's Solved these Questions
- CALORIMETRY & HEAT TRANSFERBook:DC PANDEY ENGLISHChapter:CALORIMETRY & HEAT TRANSFERExercise:Level 2 More Than One Correct
Explore 5 Videos
- BASIC MATHEMATICSBook:DC PANDEY ENGLISHChapter:BASIC MATHEMATICSExercise:Exercise
Explore 13 Videos
- CALORIMETRY AND HEAT TRANSFERBook:DC PANDEY ENGLISHChapter:CALORIMETRY AND HEAT TRANSFERExercise:Medical entrance s gallery
Explore 38 Videos
Similar Questions
Three rods of copper, brass and steel are welded togeher to from a Y -shaped structure. Area of cross-section of each rod =4cm2. End of copper rod is maintained at 100∘C whereas the ends of brass and steel are at 0∘C . Lengths of copper, brass and steel rods are 46, 13 and 12 cm respectively. The rods are thermally insulated from surroundings except at ends. Thermal conductivities of copper, brass and steel are 0.92,0.26 and 0.12 CGS units respectively. Rate of heat flow through copper rod is
View SolutionThe difference between lenghts of a certain brass rod and of a steel rod is claimed to be constant at all temperatures. Is this possible?
View SolutionThe ends of a metre stick are maintain at 100∘C and 0∘C . One end of a rod is maintained 25∘C . Where should its other end be touched on the metre stick so that there is no heat current in the rod in steady state?
View SolutionFour identical rods AB, CD, CF and DE are joined as shown in figure. The length, cross-sectional area and thermal conductivity of each rod are l, A and K respectively. The ends A, E and F are maintained at temperature T1 , T2 and T3 respectively. Assuming no loss of heat to the atmosphere, find the temperature at B.

View SolutionFour identical rods AB,CD,CFandDE are joined as shown in figure. The length, cross-sectional area and thermal conductivity of each rod are l,AandK respectively. The ends A,EandF are maintained at temperature T1 , T2 and T3 respectively. Assuming no loss of heat to the atmosphere, find the temperature at B.

View SolutionA bar of copper of length 75cm and a bar of steel of length 125cm are joined together end to end. Both are of circular cross section with diameter 2cm. The free ends of the copper and the steel bars are maintained at 100∘C and 0∘C respectively. The curved surface of the bars are thermally insulated. What is the temperature of the copper-steel junction? What is the amount of heat transmitted per unit time across the junction? Thermal conductivity of copper is 386Js−1m−1C−1 and that of steel is 46Js−1m−1C−1
View SolutionFigure shows a copper rod joined to a steel rod. The rods have equal length and and the equal cross sectional area. The free end of the copper rod is kept at 0∘C and that of the steel rod is kept at 100∘C . Find the temperature at the junction of the rods. conductivity of copper =390Wm−1C−1 and that of steel =46Wm−1C−1 .

View SolutionFigure shows a copper rod joined to a steel rod. The rods have equal length and and the equal cross sectional area. The free end of the copper rod is kept at 0∘C and that of the steel rod is kept at 100∘C . Find the temperature at the junction of the rods. conductivity of copper =390WM−1.∘C−1 and that of steel =46Wm−1.∘C−1 .

View SolutionThe ends of copper rod of length 1m and area of cross section 1cm2 are maintained at 0∘C and 100∘C. At the centre of rod, there is a source of heat of 32W. The thermal conductivity of copper is 400W/mK

View SolutionFive rods of same material and same cross-section are joined as shown. Lengths of rods ab, ad and bc are l, 2l and 3l respectively. Ends a and c are maintained at temperatures 200∘C and 0∘C respectivelly.
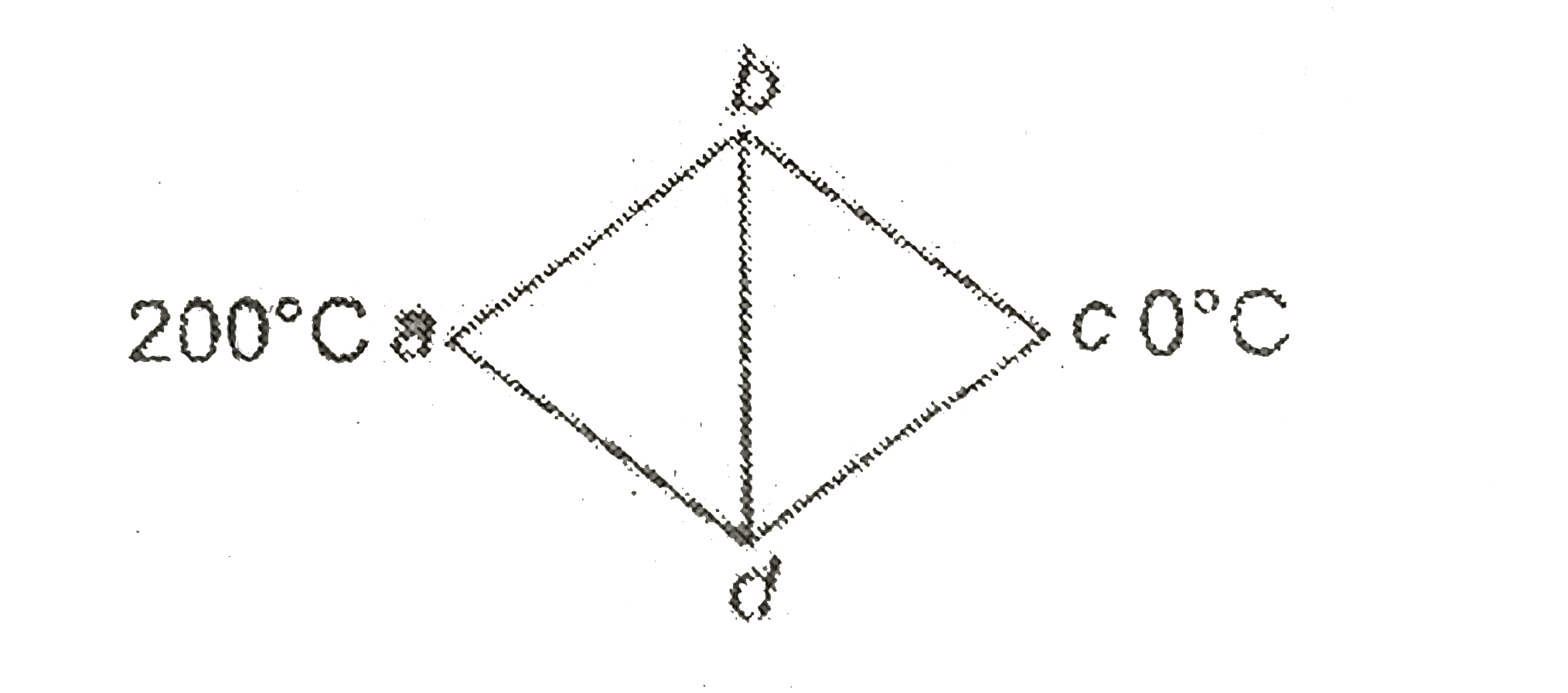
For what length x of rod dc there will be no heat flow through rod bd ?
View Solution