Two conducting cylinders of equal length but different radii are connected in series between two heat baths kept at temperatures T1=300KandT2=100K, as shown in the figure. The radius of the bigger cylinder is twice that of the smaller one and the thermal conductivities of the materials of the smaller and the larger cylinders are K1andK2 respectively. If the temperature at the junction of the two cylinders in the steady state is 200 K, then K1/K2=__________.
The correct Answer is:4
To solve the problem, we need to analyze the heat conduction through the two cylinders connected in series. Here’s a step-by-step solution:
Step 1: Understand the Setup
We have two conducting cylinders of equal length L but different radii. The smaller cylinder has a radius r1, and the larger cylinder has a radius r2=2r1. The temperatures at the ends of the cylinders are T1=300K and T2=100K. The temperature at the junction of the two cylinders is Tj=200K.
Step 2: Use the Heat Conduction Equation
The rate of heat flow through a cylindrical conductor can be given by the equation:
Q=K⋅A⋅(T1−T2)L
where Q is the heat flow, K is the thermal conductivity, A is the cross-sectional area, T1 and T2 are the temperatures at the ends, and L is the length of the cylinder.
Step 3: Calculate the Cross-Sectional Areas
The cross-sectional area A of a cylinder is given by:
A=πr2
For the smaller cylinder:
A1=πr21
For the larger cylinder:
A2=π(2r1)2=4πr21
Step 4: Set Up the Heat Flow Equations
Since the cylinders are in series, the heat flow through both cylinders must be equal:
K1⋅A1⋅(T1−Tj)L=K2⋅A2⋅(Tj−T2)L
Cancelling L from both sides gives:
K1⋅A1⋅(T1−Tj)=K2⋅A2⋅(Tj−T2)
Step 5: Substitute the Areas and Temperatures
Substituting A1 and A2:
K1⋅(πr21)⋅(300−200)=K2⋅(4πr21)⋅(200−100)
This simplifies to:
K1⋅πr21⋅100=K2⋅4πr21⋅100
Cancelling πr21⋅100 from both sides gives:
K1=4K2
Step 6: Find the Ratio K1K2
From the equation K1=4K2, we can express the ratio:
K1K2=4
Final Answer
Thus, the final answer is:
K1K2=4
We have two conducting cylinders of equal length L but different radii. The smaller cylinder has a radius r1, and the larger cylinder has a radius r2=2r1. The temperatures at the ends of the cylinders are T1=300K and T2=100K. The temperature at the junction of the two cylinders is Tj=200K.
The rate of heat flow through a cylindrical conductor can be given by the equation:
Q=K⋅A⋅(T1−T2)L
where Q is the heat flow, K is the thermal conductivity, A is the cross-sectional area, T1 and T2 are the temperatures at the ends, and L is the length of the cylinder.
The cross-sectional area A of a cylinder is given by:
A=πr2
For the smaller cylinder:
A1=πr21
For the larger cylinder:
A2=π(2r1)2=4πr21
Since the cylinders are in series, the heat flow through both cylinders must be equal:
K1⋅A1⋅(T1−Tj)L=K2⋅A2⋅(Tj−T2)L
Cancelling L from both sides gives:
K1⋅A1⋅(T1−Tj)=K2⋅A2⋅(Tj−T2)
Substituting A1 and A2:
K1⋅(πr21)⋅(300−200)=K2⋅(4πr21)⋅(200−100)
This simplifies to:
K1⋅πr21⋅100=K2⋅4πr21⋅100
Cancelling πr21⋅100 from both sides gives:
K1=4K2
From the equation K1=4K2, we can express the ratio:
K1K2=4
Thus, the final answer is:
K1K2=4
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Advanced (Archive) Level - 2 (NUMBERICAL VALUE TYPE)
7 Videos
- PROPERTIES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Advanced (Archive) Level - 2 (FILL IN THE BLANKS TYPE )
11 Videos
- PROPERTIES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Advanced (Archive) Level - 2
29 Videos
- MOVING CHARGES & MAGNETISM BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - IN-CHAPTER EXERCISE-K
10 Videos
- QUIZBOOK - VMC MODULES ENGLISHCHAPTER - QUIZEXERCISE - PHYSICS
30 Videos
Similar Questions
One end of a thermally insulated rod is kept at a temperature T1 and the other at T2. The rod is composed of two sections of length l1andl2 and thermal conductivities K1andK2 respectively. The temperature at the interface of the two section is
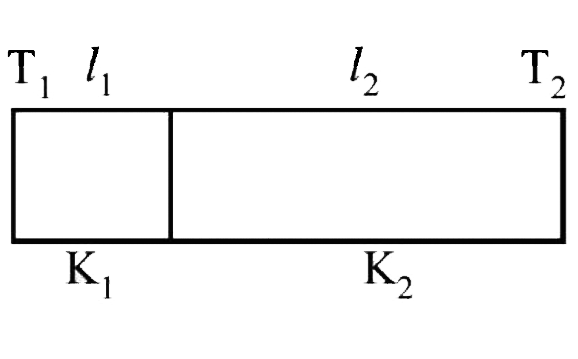
View SolutionOne end of thermally insulated rod is kept at a temperature T1 and the other at T2. The rod is composed of two section of length l1 and l2 thermal conductivities k1 and k2 respectively. The temerature at the interface of two section is
View Solution
Knowledge Check
Two walls of thickness d1andd2 and thermal conductivites K1andK2 are in contact. In the steady state, if the temperature at the outer surfaces are T1andT2 the temperature at the common wall is
AK1T1d2+K2T2d1K1d2+K2d1BK1T1+K2T2d2+d1C(K1d1+K2d2T1+T2)T1T2DK1T1d1+K2T2d2K1d1+K2d2Consider a compound slab consisting of two different material having equal thickness and thermal conductivities K and 2K respectively. The equivalent thermal conductivity of the slab is
A23KB√2KC3KD43K
One end of thermally insulated rod is kept at a temperature T1 and the other at T2. The rod is composed of two section of length l1 and l2 thermal conductivities k1 and k2 respectively. The temerature at the interface of two section is
View SolutionFind the rate of heat flow through a cross section of the rod shown in figure (θ2>θ1) . Thermal conductivity of the material of the rod is K.

View SolutionTwo identical rods are made of different materials whose thermal conductivities are K1andK2. They are placed end to end between two heat reservoirs at temperatures θ1andθ2. The temperature of the junction of the rod is

View SolutionTwo metal rods 1 and 2 of same lengths have same temperature difference between their ends. Their thermal conductivities are K1 and K2 and cross sectional areas A1 and A2 respectively. If the rate of heat conduction in 1 is four times that in 2, then
View SolutionConsider a compound slab consisting of two different material having equal thickness and thermal conductivities K and 2K respectively. The equivalent thermal conductivity of the slab is
View SolutionA slab consists of two layers of different materials of the same thickness and having thermal conductivities K1 and K2. The equivalent thermal conductivity of the slab is
View Solution
