Steel wire of length 'L' at 40∘C is suspended from the ceiling and then a mass 'm' is hung from its free end. The wire is cooled down from 40∘C→30∘C to regain its original length 'L'. The coefficient of linear thermal expansion of the steel is 10−5/∘C, Young's modulus of steel is 1011N/m2 and radius of the wire is 1mm. Assume that L>> diameter of the wire. Then the value of 'm' in kg is nearly
The correct Answer is:3
To solve the problem, we will follow these steps:
Step 1: Understand the problem
We have a steel wire of length L at 40∘C. When the wire is cooled down to 30∘C, it regains its original length L by hanging a mass m from its end. We need to find the value of m.
Step 2: Use the formula for linear thermal expansion
The change in length due to temperature change can be expressed using the linear thermal expansion formula:
ΔL=L⋅α⋅ΔT
Where:
- ΔL is the change in length,
- α is the coefficient of linear thermal expansion,
- ΔT is the change in temperature.
In this case, ΔT=40∘C−30∘C=10∘C.
Step 3: Calculate the change in length
Substituting the values into the formula:
ΔL=L⋅(10−5/∘C)⋅(10∘C)=L⋅10−4
Step 4: Relate change in length to strain
The strain ϵ in the wire is given by:
ϵ=ΔLL=L⋅10−4L=10−4
Step 5: Use Young's modulus
Young's modulus Y relates stress and strain:
Y=StressStrain
Stress can be expressed as force per unit area:
Stress=FA
Where A is the cross-sectional area of the wire. The area A for a circular wire is given by:
A=πr2
Given the radius r=1mm=1×10−3m:
A=π(1×10−3)2=π×10−6m2
Step 6: Substitute into Young's modulus equation
From the Young's modulus equation:
Y=FA⋅ϵ
Rearranging gives:
F=Y⋅A⋅ϵ
Step 7: Substitute known values
Substituting the known values:
- Y=1011N/m2
- A=π×10−6m2
- ϵ=10−4
So,
F=1011⋅(π×10−6)⋅(10−4)=π×101N
Step 8: Relate force to mass
The force F is also equal to the weight of the mass m:
F=m⋅g
Where g≈10m/s2. Therefore,
m=Fg=π×10110=πkg
Step 9: Calculate the approximate value of m
Using π≈3.14:
m≈3.14kg
Final Answer
The value of m is approximately 3.14kg.
---
We have a steel wire of length L at 40∘C. When the wire is cooled down to 30∘C, it regains its original length L by hanging a mass m from its end. We need to find the value of m.
The change in length due to temperature change can be expressed using the linear thermal expansion formula:
ΔL=L⋅α⋅ΔT
Where:
- ΔL is the change in length,
- α is the coefficient of linear thermal expansion,
- ΔT is the change in temperature.
Substituting the values into the formula:
ΔL=L⋅(10−5/∘C)⋅(10∘C)=L⋅10−4
The strain ϵ in the wire is given by:
ϵ=ΔLL=L⋅10−4L=10−4
Young's modulus Y relates stress and strain:
Y=StressStrain
Stress can be expressed as force per unit area:
Stress=FA
Where A is the cross-sectional area of the wire. The area A for a circular wire is given by:
A=πr2
Given the radius r=1mm=1×10−3m:
A=π(1×10−3)2=π×10−6m2
From the Young's modulus equation:
Y=FA⋅ϵ
Rearranging gives:
F=Y⋅A⋅ϵ
Substituting the known values:
- Y=1011N/m2
- A=π×10−6m2
- ϵ=10−4
F=1011⋅(π×10−6)⋅(10−4)=π×101N
The force F is also equal to the weight of the mass m:
F=m⋅g
Where g≈10m/s2. Therefore,
m=Fg=π×10110=πkg
Using π≈3.14:
m≈3.14kg
The value of m is approximately 3.14kg.
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Advanced (Archive) Level - 2 (NUMBERICAL VALUE TYPE)
7 Videos
- PROPERTIES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Advanced (Archive) Level - 2 (FILL IN THE BLANKS TYPE )
11 Videos
- PROPERTIES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Advanced (Archive) Level - 2
29 Videos
- MOVING CHARGES & MAGNETISM BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - IN-CHAPTER EXERCISE-K
10 Videos
- QUIZBOOK - VMC MODULES ENGLISHCHAPTER - QUIZEXERCISE - PHYSICS
30 Videos
Similar Questions
A room at 20∘C is heated by a heater of resistence 20 ohm connected to 200 V mains. The temperature is uniform throughout the room and the heati s transmitted through a glass window of area 1m2 and thickness 0.2 cm. Calculate the temperature outside. Thermal conductivity of glass is 0.2cal/mC∘ s and mechanical equivalent of heat is 4.2J/cal.
View SolutionThe variation of temperature of a material as heat is given to it at a constant rate is shown in the figure. The material is in solid state at the point O. The state of the material at the point P is…..
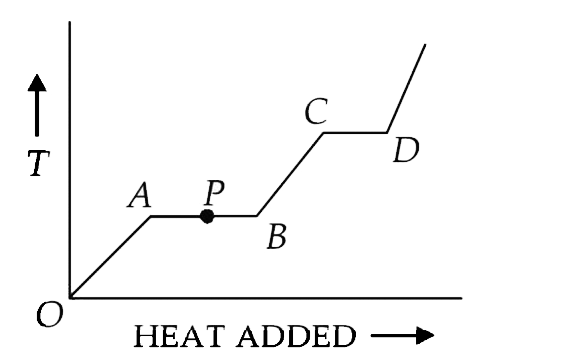
View SolutionA wall is made of equally thick layers A and B of different matierals. Thermal conduvtivity of A is twice that of B. In the stedy state, the temperature difference across the wall is 36∘C . The temperature difference across the layer A is
View SolutionThe angle of dip is the angle
View SolutionA mass m of radius r is rolling horizontally without any slip with a linear speed v. It then rolls up to a height given by 34v2g
View SolutionAt 40^(@)C a brass wire of 1mm radius is hung from the ceiling. A small mass, M is hung from the free end of the wire. When the wire is cooled down from 40^(@)C to 20^(@)C it regains its original length of 0.2 m the value of M is close to (coefficient of linear expansion and young's modulus of brass are 10^(-5)//.^(@)C and 10^(11)//N//m^(2) respectively g=10ms^(-2))
View SolutionSteel wire of length 'L' at 40^@C is suspended from the ceiling and then a mass 'm' is hung from its free end. The wire is cooled down from 40^@C to 30^@C to regain its original length 'L'. The coefficient of linear thermal expansion of the steel is 10^-5//^@C , Young's modulus of steel is 10^11 N//m^2 and radius of the wire is 1mm. Assume that L gt gt diametere of the wire. Then the value of 'm' in kg is nearly
View SolutionA steel wire of length 20 cm and uniform cross-section 1mm^(2) is tied rigidly at both the ends. If the temperature of the wire is altered from 40^(@)C to 20^(@)C , the change in tension. [Given coefficient of linear expansion of steel is 1.1xx10^(5) .^(@)C^(-1) and Young's modulus for steel is 2.0xx10^(11) Nm^(-2) ]
View SolutionAn aluminium wire and a steel wire of the same length and cross section are joined end to end. The composite wire is hung from a rigid support and the load is suspended at the free end. If Y_(AL) = 7xx10^(10) N//m^(2) and Y_("steel") = 7xx10^(11) N//m^(2) , the ratio of elongation of aluminium and steel wires is
View SolutionA steel wire of length 1m, and radius 0.1mm is elongated by 1mm due to a weight of 3.14kg. If g = 10 m//s^(2) , the Young's modulus of the steel wire will be
View SolutionL लम्बाई का स्टील का तार, जो 40∘C तापमान पर है, को छत से लटका कर उसके मुक्त सिरे पर द्रव्यमान m संलग्न किया जाता है | जब तार को ठण्डा करके उसका तापमान 40∘C से 30∘C लाने पर उसकी लम्बाई फिर से L हो जाती है | स्टील का तापीय प्रसार गुणांक 10−5/.∘C है, यंग प्रत्यास्थता गुणांक 1011 न्यूटन मी−2 है तथा तार की त्रिज्या 1 मिमी है | मानें कि L>> तार का व्यास m का किग्रा में मान लगभग है |
View Solution40∘C तापमान पर 1mm त्रिज्या का पीतल का एक तार छत से लटकाया गया है। तार के मुक्त सिरे से M द्रव्यमान के एक छोटे पिण्ड को लटकाया गया है। जब तार 40∘C को 20∘C से पर ठण्डा करते है, तो वह वापस अपनी पुरानी लम्बाई 0.2 m को प्राप्त कर लेता है। M का निकटतम मान होगा (पीतल का रेखीय प्रसार गुणांक तथा यंग प्रत्यास्थ गुणांक क्रमशः है
105/∘C तथा 1011N/m एवं g=10ms−2)
View SolutionThe pressure that has to be applied to the ends of a steel wire of length 10 cm to keep its length constant when its temperature is raised by 100∘C is (For steel, Young's modulus is 2×1011N⋅m−2 and coefficient of linear expansion is 1.1×10−5K−1)
View SolutionA copper wire of length l and radius 2 mm is suspended from a fixed support vertically and a mass m is hung from its other end. The wire initially at 30^@C is cooled down to 20^@C to bring it back to its original length l . The coefficient of linear thermal expansion of the copper is 1.7 xx 10^(-5) "'^@C^(-1) . If l >> the diameter of wire,then find the value of m/5 in kg close to nearest integer. Take, g = 10 m//s^2 , Y = 1.1 xx 10^11 N//m^2
View SolutionSteel wire of length 'L' at 40∘C is suspended from the ceiling and then a mass 'm' is hung from its free end. The wire is cooled dowa from 40∘C to 30∘C to regain its original length 'L'. The coefficient of linear thermal expansiou of the steel is 10−5/∘C, Young's modulus of steel is 1011N/m2 and radius of the wire is 1 mm. Assume that L>> diameter of the wire. Then the value of 'm' in kg is nearly
View SolutionThe pressure that has to be applied to the ends of a steel wire of length 10 cm to keep its length constant when its temperature is raised by 100^(@)C is : (For steel Young's modulus is 2 xx 10^(11) N m^(2) and coefficient of themal expansion is 1.1 xx 10^(-5)K^(-1))
View Solution
