If the absorption coefficient and reflection coefficient of a surface of a body are 0.4 and 0.6 respectively then:-
Emissive power will be 0.2
Transmission power will be 0.2
Body will be be totally transparent
Body will be totally opaque.
The correct Answer is:D
To solve the problem, we need to analyze the given coefficients: the absorption coefficient (A) and the reflection coefficient (R). The question provides us with the values:
- Absorption coefficient (A) = 0.4
- Reflection coefficient (R) = 0.6
We need to find the transmissive power (T) and determine the nature of the body (whether it is opaque or not).
1. Understand the relationship between absorption, reflection, and transmission:
The sum of the absorption coefficient (A), reflection coefficient (R), and transmissive coefficient (T) for a surface must equal 1. This can be expressed mathematically as:
A+R+T=1
2. Substitute the known values into the equation:
We know:
- A = 0.4
- R = 0.6
Therefore, substituting these values into the equation gives:
0.4+0.6+T=1
3. Simplify the equation:
Combine the known coefficients:
1+T=1
4. Solve for the transmissive power (T):
To find T, we can rearrange the equation:
T=1−1=0
5. Interpret the result:
Since the transmissive power (T) is 0, this indicates that the body does not allow any light to pass through it. Therefore, the body is completely opaque.
Conclusion:
The body is totally opaque because it does not transmit any light.
- Reflection coefficient (R) = 0.6
The sum of the absorption coefficient (A), reflection coefficient (R), and transmissive coefficient (T) for a surface must equal 1. This can be expressed mathematically as:
A+R+T=1
We know:
- A = 0.4
- R = 0.6
Therefore, substituting these values into the equation gives:
0.4+0.6+T=1
Combine the known coefficients:
1+T=1
To find T, we can rearrange the equation:
T=1−1=0
Since the transmissive power (T) is 0, this indicates that the body does not allow any light to pass through it. Therefore, the body is completely opaque.
The body is totally opaque because it does not transmit any light.
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -0310videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - ASSERTION-REASON36videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -0165videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II66videos
CURRENT ELECTRICITY
- BOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 49videos
GRAVITATION
Similar Questions
A horizontal force just sufficient to move a body of mass 4kg lying on a rought horizontal surface is applied on it .The coefficient of static and kinetic friction the body and the surface are 0.8and0.6 respectively If the force contines to act even after the block has started moving the acceleration of the block in ms−2 is (g=10ms−2)
View SolutionA body of weight 64 N is pushed with just enough force to start it moving across a horizontal floor and the same force continues to act afterwards. If the coefficients of static and dynamic friction are 0.6 and 0.4 respectively, the acceleration of the body will be (Acceleration due to gravity = g)
View Solution
Knowledge Check
- Question 1 - Select One
For a body on a horizontal surface, coefficients of static and kinetic frictions are 0.4 and 0.2 respectively. When the body is in uniform motion on the surface, a horizontal force equal in magnitude to limiting friction is applied on it. The acceleration produced is
 A0.4gB0.1 gC0.2 gD0.6 g
A0.4gB0.1 gC0.2 gD0.6 g - Question 2 - Select One
If the two regression coefficients are - 0.4 and -1.6, then the coefficient of correlations is
A0B−0.9C0.8D1
A slab of 40kg lying on a frictionales floor and a block of 10 kg rests on the slab as shown in the figure. The coefficients of static and kinetic friction between the slab and the block are 0.6 and 0.4 respectively. If a force of 100N is applied on the block, then the acceleration the slab will be (g=10m/s2)
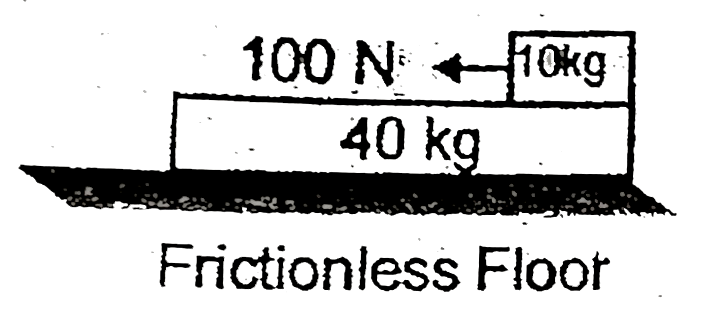 View Solution
View SolutionThe coefficient of static friction between two surfaces depend on
View SolutionFor any material, If R , T and A represent the reflection coefficient, transparent coefficient and absorption coefficient respectively, then for a blackbody which one of the following is true
View SolutionA body of mass 60 kg is dragged with just enough force to start moving on a rough surface with coefficient of static and kinetic frictions 0.5 and 0.4 respectively . On applying the same force , what is the acceleration ?
View SolutionA 60 kg body is pushed with just enough force to start it moving across a floor and the same force continues to act afterwards. The coefficient of static friction and sliding friction are 0.5 and 0.4 respectively. The acceleration of the body is
View SolutionA 60kg is pushed horizontaly with just enough force to start it moving across a floor and the same force continues to act afterwards. The coefficient of static friction and sliding friction are 0.5and 0.4 respectively the accleration of the body is
View Solution
