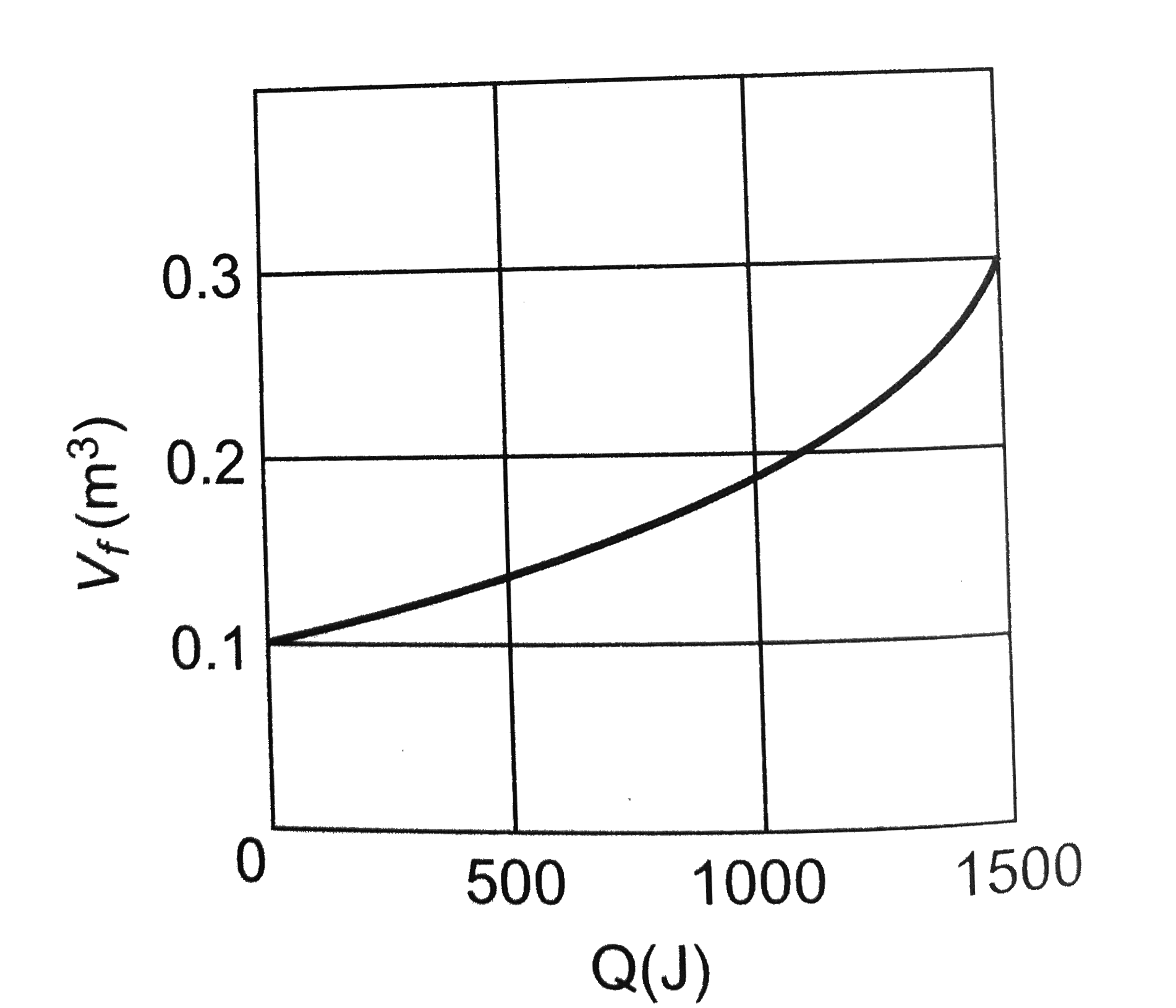
Suppose 0.5 mole of an ideal gas undergoes an isothermal expansion an energy is added to it as heat Q.
Graph shows the final volume V1 versus Q. The temperature of the gas is (use ln9=2 and R=25/3J/mol−K)
_S01_088_Q01.png)
293K
360K
386K
412K
The correct Answer is:B
Q=W=nRTlnVfVt
T=QnRlnVf/Vt=15000.5×25/3×ln3
=15000.5×25/3×1=360K
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -03
10 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - ASSERTION-REASON
36 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -01
65 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
Suppose 0.5 moles of an ideal gas undergoes an isothermal expansion as energy is added to it as heat Q. graph shows the final volume Vf versus Q. the temperature of the gas is (use In9=2 and R=253J/mol−K)
View SolutionSuppose 0.5 moles of an ideal gas undergoes an isothermal expansion as energy is added to it as heat Q. graph shows the final volume Vf versus Q. the temperature of the gas is (useIn9=2andR=253J/mol−K)

View Solution
Knowledge Check
The work done, W, during an isothermal process in which the gas expands from an intial volume V1, to a final volume V2 is given by (R : gas constant, T : temperature )
AR(V2−V1)logeT1T2BR(T2−T1)loge(V1V2)CRTloge[V2V1]D2RTloge[V1V2]
1 mole of an ideal gas undergoes an isothermal reversible expansion form 10 atm to 1 atm at 300 K. What will be the work done ?
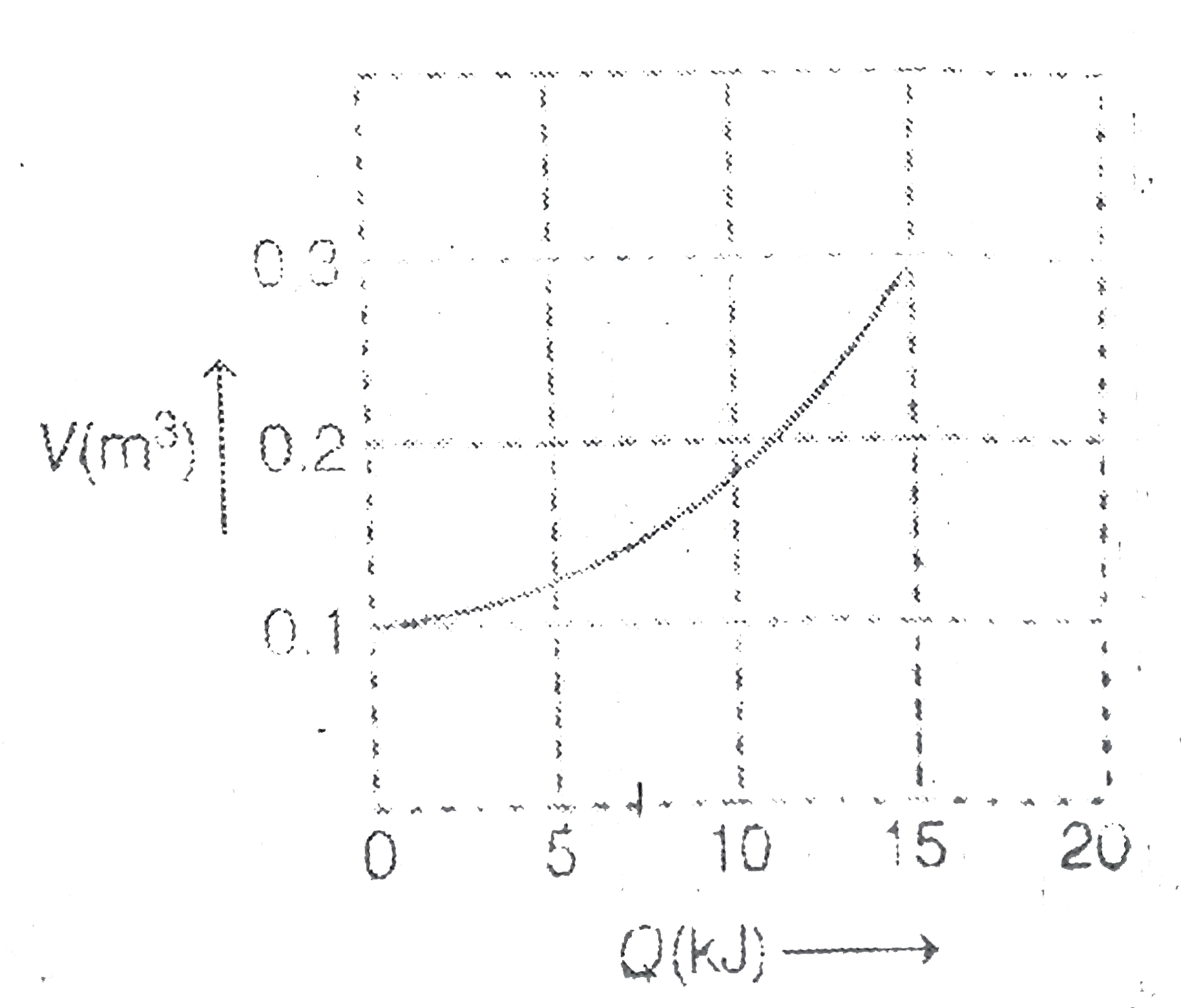
View SolutionConsider isothermal expansion of 0.5 mole of an ideal gas when Q amount of heat is added to it. Following graph shows variation in volume V with Q. Find the temperature of the gas
(ln 3≈10,R=253J/mole−K)
View SolutionOne mole of an ideal gas undergoes a process
P=P0−αV2
where α and P0 are positive constant and V is the volume of one mole of gas
Q. When temperature is maximum, volume is
View SolutionOne mole of an ideal gas undergoes a process
P=P0−αV2
where α and P0 are positive constant and V is the volume of one mole of gas
Q. When temperature is maximum, volume is
View SolutionOne mole of an ideal gas undergoes a process
P=P0−αV2
where α and P0 are positive constant and V is the volume of one mole of gas
Q. The maximum attainable temperature is
View SolutionAt 27∘C two moles of an ideal monatomic gas occupy a volume V. The gas expands adiabatically to a volume 2V. Calculate
(a) final temperature of the gas
(b) change in its internal energy and
[ R=8.31J/mol−K]
View Solution1mol of an ideal gas at 400K and 10atm is allowed to expand, adiabatically, against 2.0atm external pressure. Find the final temperature of the gas. [Use: Cv=52R]
View Solution
