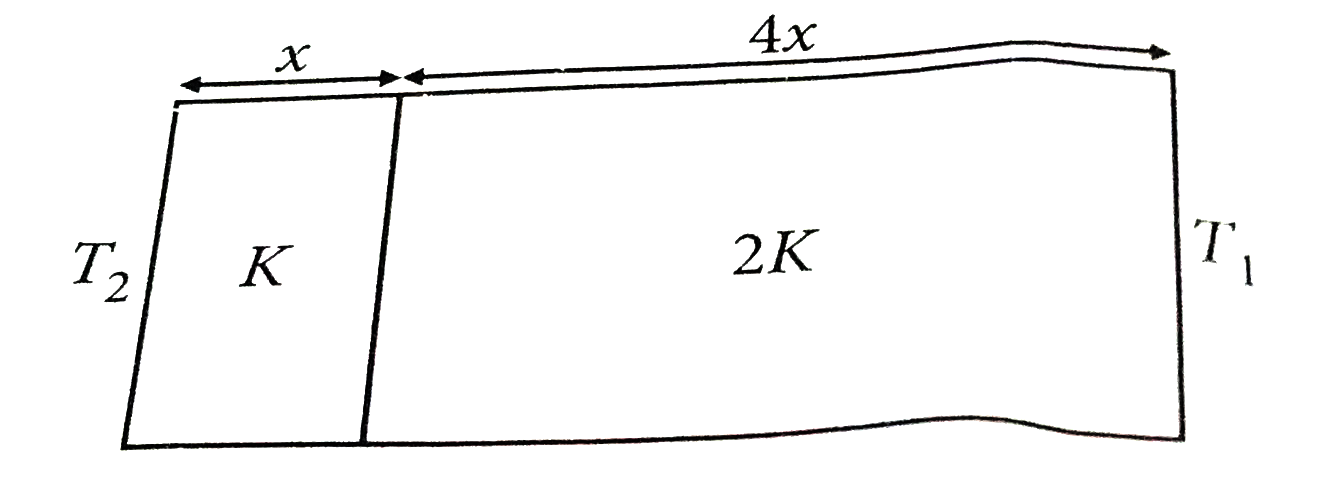
The temperature of the two outer surface of a composite slab, consisting of two materials having coefficients of thermal conductivity K and 2K and thickness x and 4x, respectively are T2and T1(T2>T1). The rate of heat transfer through the slab, in a steady state is (A(T2−T1)Kx)f, with f equal to
1
1/2
2/3
1/3
The correct Answer is:D
∗Q=T2−T1xKA+4x2KA=KA(T2−T1)3x=[KA(T2−T1)x]f
then f = 1/3
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -03
10 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - ASSERTION-REASON
36 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -01
65 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
The temperature of the two outer surfaces of a composite slab, consisting of two materials having coefficients of thermal conductivity K and 2K and thicknesses x and 4x, respectively are T2 and T1(T2>T1). The rate of heat of heat transfer through the slab, in ? steady state is [(AT2−T1x]f, with f equal to :-

View SolutionThe temperature of the two outer surfaces of a composite slab consisting of two materials having coefficient of thermal conductivity K and 2K and thickness x and 4x respectively are T2 and T1(T2>T1). The rate of heat transfer through the slab in steady state is (AK(T2−T1)x)f. where, f is equal to
 .
.
View Solution
Knowledge Check
The temperature of the two outer surfaces of a composite slab, consisting of two materials having coefficients of thermal conductivity K and 2K and thickness x and 4x respectively. Temperatures on the opposite faces of composite slab are T1andT2 where T2>T1, as shown in fig. what is the rate of flow of heat through the slab in a steady state?
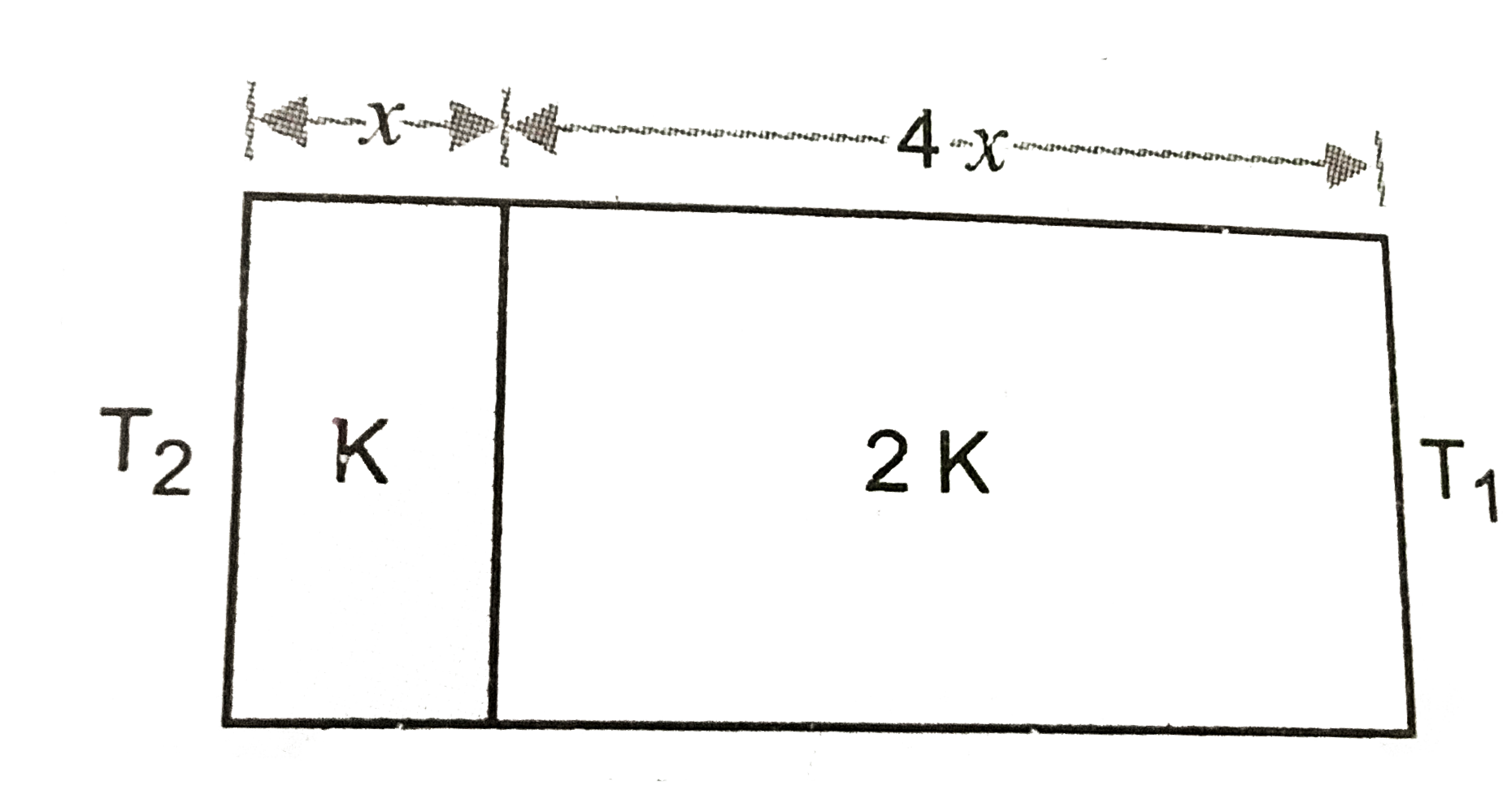 A1B12C23D13
A1B12C23D13Consider a compound slab consisting of two different material having equal thickness and thermal conductivities K and 2K respectively. The equivalent thermal conductivity of the slab is
A23KB√2KC3KD43K
The two ends of a rod of length L and a uniform cross-sectional area A are kept at two temperature T1 and T2 (T1>T2). The rate of heat transfer. dQdt, through the rod in a steady state is given by
View SolutionConsider a compound slab consisting of two different material having equal thickness and thermal conductivities K and 2K respectively. The equivalent thermal conductivity of the slab is
View SolutionTwo materials having coefficients of thermal conductivity '3k' and 'k' and thickness 'd' and '3d' respectively, are joined to form a slab as shown in the figures. The temperatures of the outer surfaces are θ2 and θ1 respectively (θ2>θ2). The temperature at the interface is :
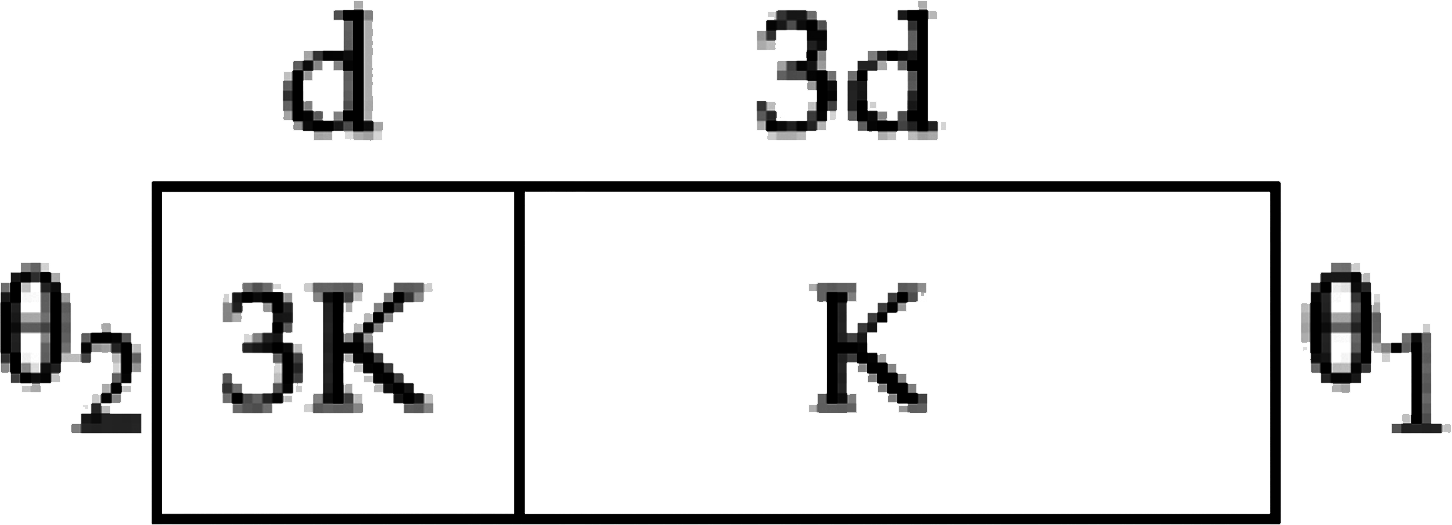
View SolutionThree rods of same cross-section but different length and conductivity are joined in series . If the temperature of the two extreme ends are T1andT2(T1>T2) find the rate of heat transfer H.

View SolutionA composite slab is made of two parallel layers of two different materials of thermal conductivities K1andK2 are of same thickness. Show that the equivalent thermal conductivity of the slab is 2K1K2K1+K2
View SolutionA slab consists of two layers of different materials of the same thickness and having thermal conductivities K1 and K2. The equivalent thermal conductivity of the slab is
View Solution
