Three bodies A,B and C have equal surface area and thermal emissivities in the ratio eA:eB:eC=1:12:14. All the three bodies are radiating at same rate. Their wavelengths corresponding to maximum intensity are αA,αB and αC respectively and their temperatures are TA,TB and TC on kelvin scale , then select the incorrect statement
√TATC=TB
√λAλC=λB
√eATA√eCTC=eBTB
√eAλATA.eBλBTB=eCλCTC
The correct Answer is:D
To solve the problem, we need to analyze the relationship between the emissivities, temperatures, and the wavelengths corresponding to maximum intensity for the three bodies A, B, and C.
1. Understanding Emissivity and Power Radiated:
- The emissivities of bodies A, B, and C are given in the ratio:
eA:eB:eC=1:12:14
- Let’s denote:
eA=1,eB=12,eC=14
2. Using Stefan-Boltzmann Law:
- The power radiated by each body can be expressed using the Stefan-Boltzmann Law:
P=eσAT4
- Since all three bodies are radiating at the same rate, we can write:
eAσT4A=eBσT4B=eCσT4C
3. Setting Up the Equations:
- From the above, we can simplify:
T4A=eB⋅T4B/eA
T4B=eC⋅T4C/eB
- Substituting the emissivity values:
T4A=1/21T4B=12T4B
T4B=1/41/2T4C=12T4C
4. Relating Temperatures:
- From T4A=12T4B, we get:
TA=(12)1/4TB=TB√(4)2
- From T4B=12T4C, we get:
TB=(12)1/4TC=TC√(4)2
5. Finding Relationships:
- Now substituting back, we can express TA in terms of TC:
TA=TC√(4)2⋅√(4)2=TC√2
6. Wavelengths of Maximum Intensity:
- The wavelengths corresponding to maximum intensity are given by Wien's displacement law:
λmax∝1T
- Thus, we have:
αA∝1TA,αB∝1TB,αC∝1TC
- Substituting the temperature relationships:
αA∝√2⋅αC
αB∝√(4)2⋅αC
7. Conclusion:
- The incorrect statement can be identified by checking the relationships derived above. The relationships between the wavelengths and temperatures must hold true based on the derived equations.
- The emissivities of bodies A, B, and C are given in the ratio:
eA:eB:eC=1:12:14
- Let’s denote:
eA=1,eB=12,eC=14
- The power radiated by each body can be expressed using the Stefan-Boltzmann Law:
P=eσAT4
- Since all three bodies are radiating at the same rate, we can write:
eAσT4A=eBσT4B=eCσT4C
- From the above, we can simplify:
T4A=eB⋅T4B/eA
T4B=eC⋅T4C/eB
- Substituting the emissivity values:
T4A=1/21T4B=12T4B
T4B=1/41/2T4C=12T4C
- From T4A=12T4B, we get:
TA=(12)1/4TB=TB√(4)2
- From T4B=12T4C, we get:
TB=(12)1/4TC=TC√(4)2
- Now substituting back, we can express TA in terms of TC:
TA=TC√(4)2⋅√(4)2=TC√2
- The wavelengths corresponding to maximum intensity are given by Wien's displacement law:
λmax∝1T
- Thus, we have:
αA∝1TA,αB∝1TB,αC∝1TC
- Substituting the temperature relationships:
αA∝√2⋅αC
αB∝√(4)2⋅αC
- The incorrect statement can be identified by checking the relationships derived above. The relationships between the wavelengths and temperatures must hold true based on the derived equations.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -03
10 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - ASSERTION-REASON
36 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -01
65 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
The plots of intensity versus wavelength for three black bodies at temperature T1,T2andT3 respectively are as shown. Their temperatures are such that
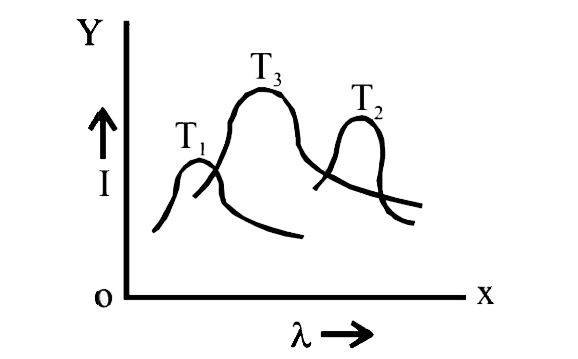
View SolutionThe plots of intensity versus wavelength for three black bodies at temperatures T1,T2 and T3 respectively are shown in Their temperatures are shown in How their temperatures are related ?
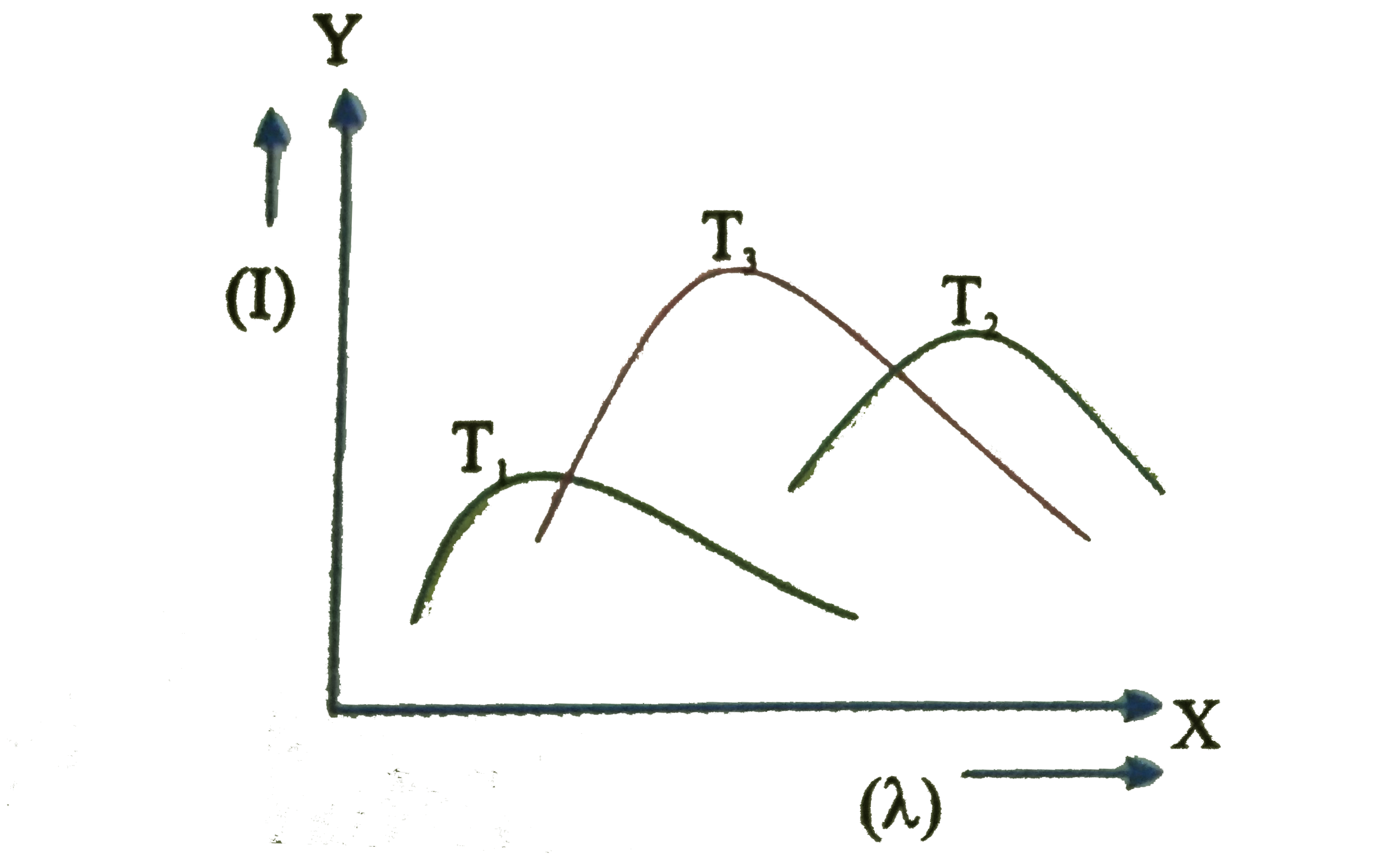 .
.
View Solution
Knowledge Check
The plots of intensity versus wavelength fro three black bodies at temperatures T1,T2 and T3 respectively and shown in Fig. 15.11.1. Their temperatures are such that
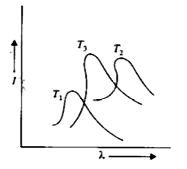 AT1>T2>T3BT1>T3>T2CT2>T3>T1DT3>T2>T1
AT1>T2>T3BT1>T3>T2CT2>T3>T1DT3>T2>T1Three stars A,B,C have surface temperatures TA,TB and TC. A appaears bluish, B appears reddish and C appears yellowish. We can conclude that
ATA>TC>TBBTA>TB>TCCTB>TC>TADTC>TB>TAEnergy levels A,B,C of a certain atom corresponding to increasing values of energy i.e., EA<EB<EC. If λ1,λ2,λ3 are the wavelengths of radiations correspnding to the transitions C to B,B to A and C to A respectively, which of the following statements is correct?
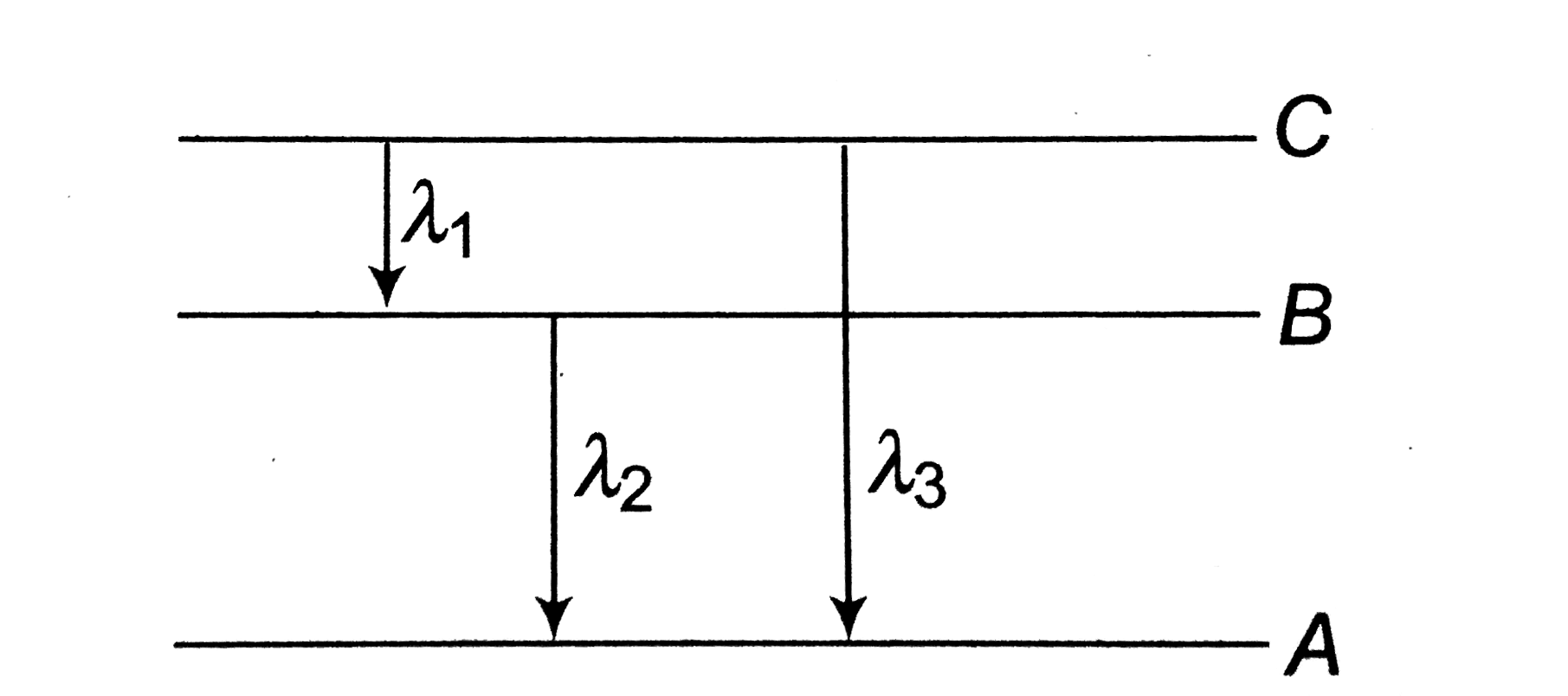 Aλ3=λ1+λ2Bλ1+λ2+λ3=0Cλ23=λ21+λ22Dλ=λ1λ2λ1+λ2
Aλ3=λ1+λ2Bλ1+λ2+λ3=0Cλ23=λ21+λ22Dλ=λ1λ2λ1+λ2
Two electric lamps A and B radiate the same power. Their filaments have the same diemensions, and have emissivities. eA and eB. Their surface tempratures are TA an TB. The ratio TA/TB will be equal to
View SolutionThree isothermal plots (P versus V) A, B and C are plotted at three temperature T1,T2andT3 respectively
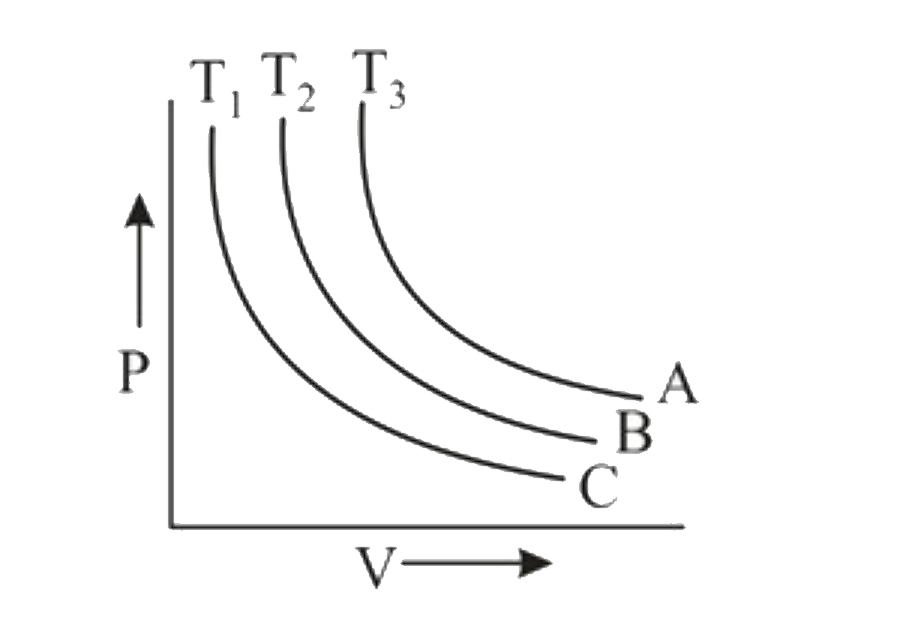
The correct order of the temperature will be
View SolutionTwo bodies A and B having equal surface areas are maintained at temperatures 10∘C . And 20∘C . The thermal radiation emitted in a given time by A and B are in the ratio
View SolutionConsider three square matrices A, B and C of order 3 such that AT=A−2BandBT=B−4C, then the incorrect option is
View SolutionEnergy levels A,B,C of a certain atom corresponding to increasing values of energy i.e., EA<EB<EC. If λ1,λ2,λ3 are the wavelengths of radiations correspnding to the transitions C to B,B to A and C to A respectively, which o fthe following statements is correct?

View Solution
