In Newton's law of cooling dθdt=−k(θ−θ0) the constant k is proportional to .
A, surface area of the body
S, specific heat of the body
1m, m being mass of the body
e, emissity of the body
The correct Answer is:A, C
To determine what the constant k in Newton's law of cooling is proportional to, we need to analyze the factors that influence the rate of heat transfer between an object and its surroundings.
Step 1: Understanding Newton's Law of Cooling
Newton's law of cooling states that the rate of change of temperature of an object is proportional to the difference in temperature between the object and its surroundings. Mathematically, this is expressed as:
dθdt=−k(θ−θ0)
where:
- θ is the temperature of the object,
- θ0 is the ambient temperature,
- k is the cooling constant.
Step 2: Identifying Factors Affecting k
The cooling constant k is influenced by several physical factors:
1. Surface Area: The larger the surface area of the object, the more heat can be transferred to or from the surroundings. Therefore, k is proportional to the surface area of the object.
2. Specific Heat: The specific heat of the material affects how quickly it can change temperature. Materials with lower specific heat will change temperature more rapidly, influencing the value of k.
3. Emissivity: This is a measure of how effectively a surface emits thermal radiation. A higher emissivity means that the surface can radiate heat more efficiently, which also affects the value of k.
Step 3: Conclusion
From the analysis, we conclude that the constant k is proportional to the following factors:
- Surface area
- Specific heat
- Emissivity
Thus, we can summarize that:
k∝Surface Area, Specific Heat, Emissivity
Newton's law of cooling states that the rate of change of temperature of an object is proportional to the difference in temperature between the object and its surroundings. Mathematically, this is expressed as:
- θ is the temperature of the object,
- θ0 is the ambient temperature,
- k is the cooling constant.
The cooling constant k is influenced by several physical factors:
From the analysis, we conclude that the constant k is proportional to the following factors:
- Surface area
- Specific heat
- Emissivity
Topper's Solved these Questions
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:EXERCISE -01
Explore 65 Videos
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:EXERCISE -02
Explore 82 Videos
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:subjective
Explore 14 Videos
- CURRENT ELECTRICITYBook:ALLENChapter:CURRENT ELECTRICITYExercise:EX.II
Explore 66 Videos
- GRAVITATIONBook:ALLENChapter:GRAVITATIONExercise:EXERCISE 4
Explore 9 Videos
Similar Questions
A hot body placed in a surrounding of temperature θ0 obeys Newton's law of cooling dθdt=−k(θ−θ0) . Its temperature at t=0 is θ1 the specific heat capacity of the body is s and its mass is m. Find
(a) the maximum heat that the body can lose and
(b) the time starting from t=0 in which it will lose 90% of this maximum heat.
View SolutionIn newton's law of cooling in the form
dΔθdt=−kΔθ
What factors does the constant k depend upon? What are the dimensions of k?
View Solution
Knowledge Check
Assertion: According to Newton's law of cooling, the rate of loss of heat, −dQ/dt of the body is directly proportional to the difference of temperature.
Reason :This law holds for all type of temperature differences.Alaw of thermometryBNewton's law of coolingClaw of calorimetryDzeroth law
Newton's law of cooling is a special case of
View SolutionAccording to Newton’s law of cooling, the rate of cooling of a body is proportional to (Δθ)n , where Δθis the difference of the temperature of the body and the surrounding, and n is equal to :
View Solution∫dθ(sinθ−2cosθ)(2sinθ+cosθ)
View SolutionA liquid in a beaker has temperature θ(t) at time t and θ0 is temperature of surroundings, then according to Newton's law of cooling the correct graph between loge(θ−θ0) and t is :
View SolutionAccording to ‘Newton’s Law of cooling’, the rate of cooling of a body is proportional to the
View SolutionInstantaneous temperature difference between cooling body and the surroundings obeying Newton's law of cooling is θ. Which of the following represents the variation of In θ with time t?
View SolutionA body cools in a surrounding which is at constant temperature of θ0. Assume that it obeys Newton's law of colling. Its temperature θ is plotted against time t. Tangents are drawn to the curve at the points P(θ=θt) and Q(θ=θ2). These tangents meet the time axis at angles of ϕ2 and ϕ1, as shown
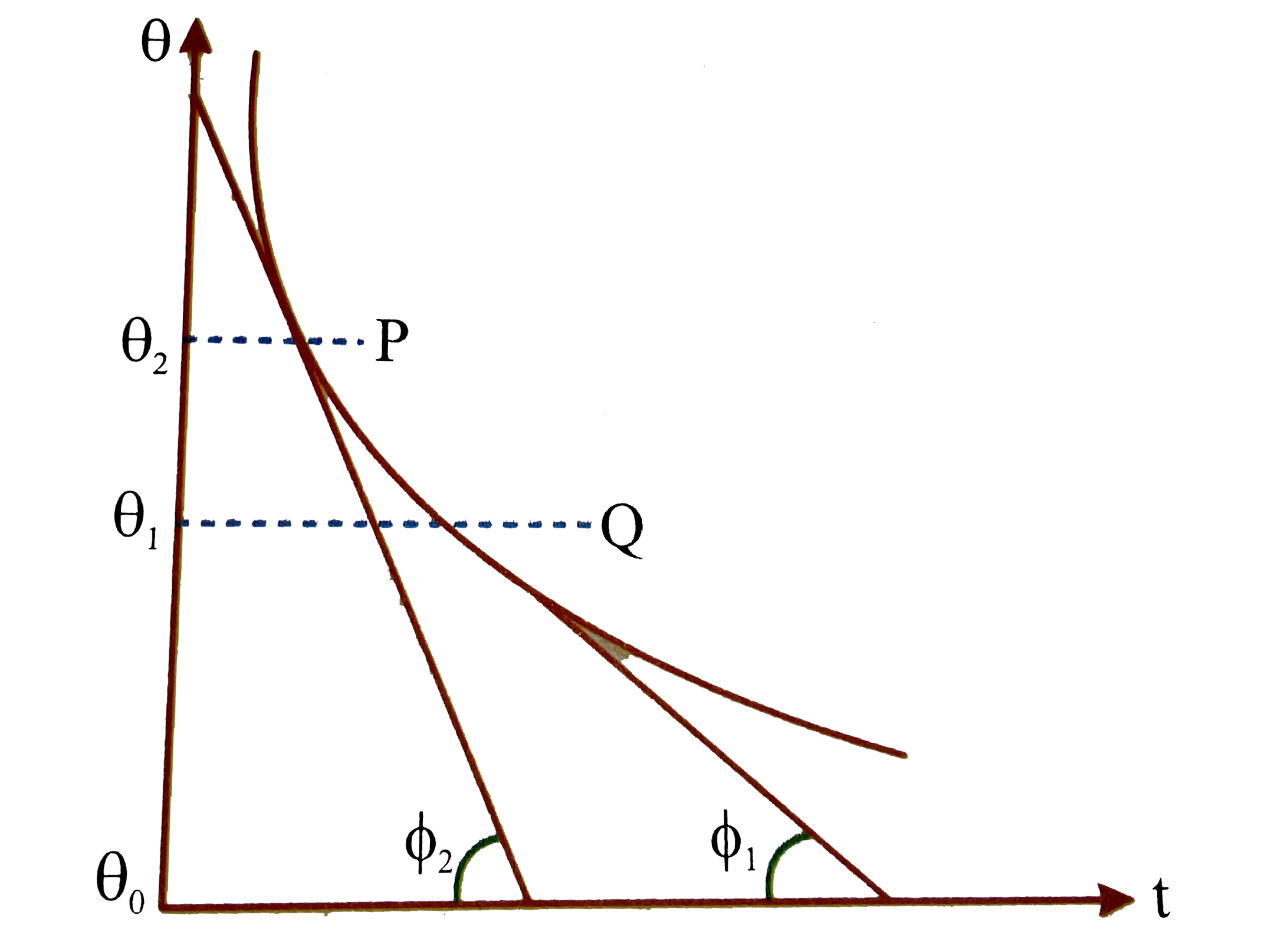
View Solution

