A prism of refractive index n1 & another prism of reactive index n2 are stuck together without a gap as shown in the figure.The angle of the prisms are as shown. n1&n2depend onλ,the wavelength of light according to n1=1.20+10.8×104λ2&n2=1.45+1.80×104λ2 where λ is in nm.
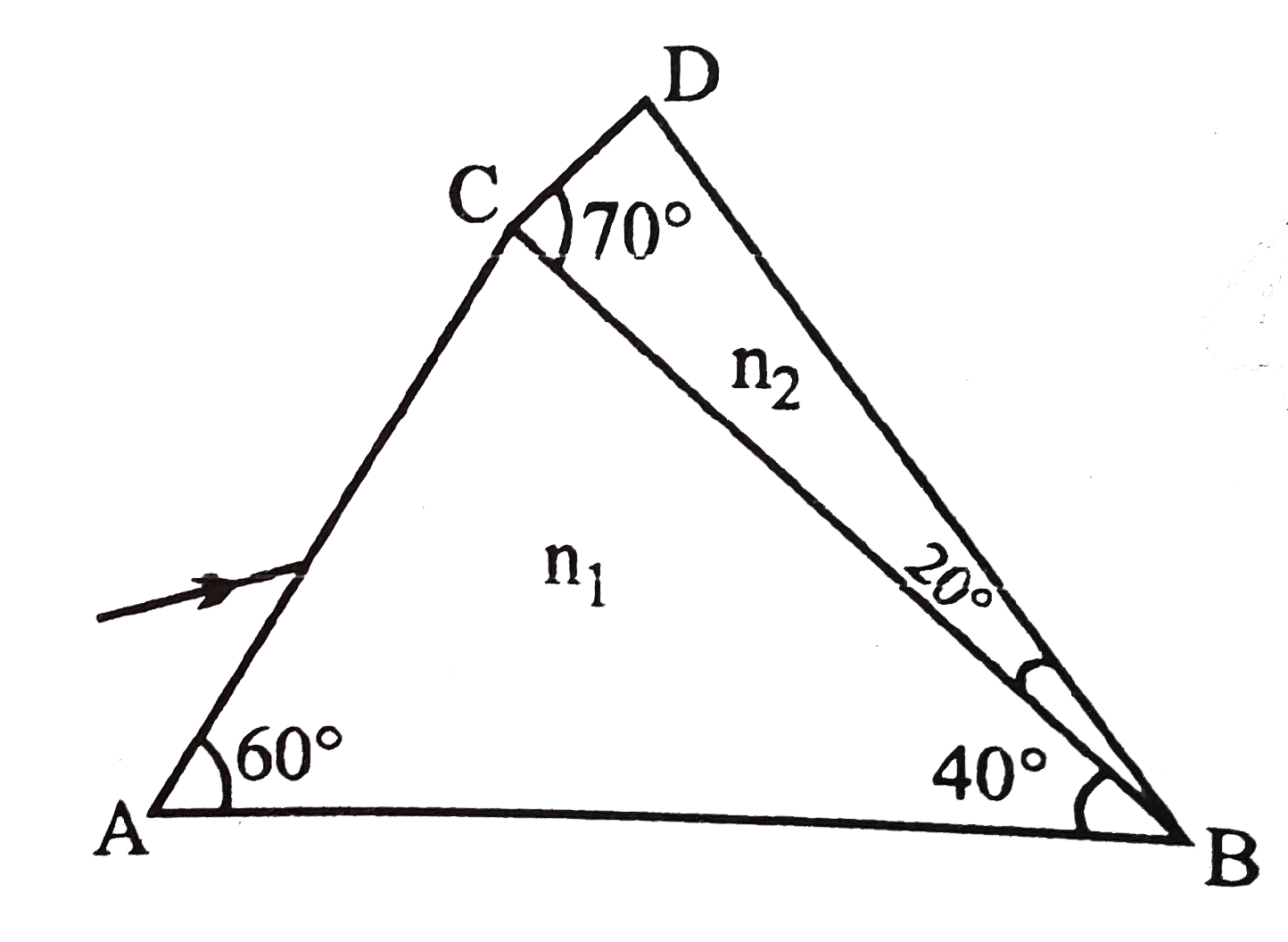
(i)Calculate the wavelength λ0for which rays incident at any angle on the interfaceBCpass through without bending at that interface.
The correct Answer is:(a) 600 nm (b) sin−1(3/4)
n1=1.20+10.8×104λ2 and
n2=1.45+1.80×104λ2 Here , λ is in nm.
(a) The incident ray will not deviate at BC if n1=n2
⇒1.20+10.8×104λ20 = 1.45 + (1.80 xx 10^(4))/(lambda_(0)^(2)) (lambda = lambda_(0))<br>implies (9 xx 10^(4))/(lambda_(0)^(2)) = 0.25 implies lambda_(0) = (3 xx 10^(2))/(0.5) "or" lambda_(0) = 600nm<br>(b)Thegivensystemisapartofanequiolateralprismofprism∠60^(@)asshown∈thefigure.<br>Atminiμmdeviation<br>r_(1) = r_(2) = (60^(@))/(2) = 30^(@)=r(say)<br>therefore n_(1) = ("sini")/("sinr")<br>therefore "sini" = n_(1)"sin"30^(@)<br>"sin i" = {1.20 + (10.8 xx 10^(4))/((600)^(2))}((1)/(2)) = (1.5)/(2) = (3)/(4)<br>(lambda = lambda_(0) = 600 "nm")<br>implies i = sin^(-1) (3//4)
_E01_244_S01.png)
Topper's Solved these Questions
Similar Questions
∫423x2+1(x2−1)3dx=λn2 where λ,n∈N and gcd(λ,n)=1, then find the value of λ+n
View Solution
A right angled triangular prism of refractive index μ1 is kept floating on a liquid (surface) having refractive index μ2. The condition such tat light incident normally passes through base of prism as shown in figure.
View Solution
Knowledge Check
A thin prism of angle 15∘ made of glass of refractive index μ1=1.5 is combined with another prism of glass of refractive index μ2=1.75. The combination of the prism produces dispersion without deviation. The angle of the second prism should be
A5∘B7∘C10∘D12∘A ray of light passes through an equilateral prism (refractive index 1.5) such that angle of incidence is equal to angle of emergence and the latter is equal to 3/4th of the angle of prism. Calculate the angle of deviation.
A60∘B30∘C45∘D120∘
A thin prism P1 with angle6∘ and made from glass of refractive index 1.54 is combined with another thin prism P2 of refractive index 1.72 to produce dispersion without deviation. The angle of prism P2 will be
View SolutionA prism having an apex angle of 4∘ and refractive index of 1.50 is located in front of a vertical plane mirror as shown in the figure. A horizontal ray of light is incident on the prism. The total angle through which the ray is deviated is:
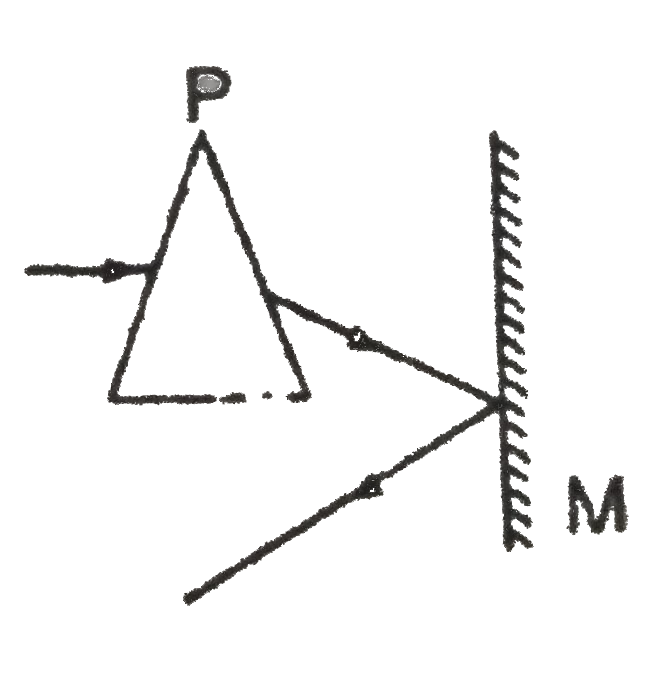
View SolutionA prism of angle A=1∘ has a refractive index μ=1.5 . A good estimate for the minimum angle of deviation ( in degrees ) is close to N/10 value of N is ________ .
View SolutionA glass prism is immersed in a hypothetical liquid. The curves showing the refractive index n as a function of wavelength λ for glass and liquid are as shown in Figs. When a ray of white light is incident on the prism parallel to the base

View SolutionA light ray moving in medium-I (of refractive index n1) is incident on interface of two media and it is totally internally reflected at the interface. Now, refractive index n2 of medium-II is decreased, then

View SolutionA right angles prism (45∘,90∘,45∘) of refractive index n has a plate of refractive index (n1<n) cemented to its diagonal face. The assembley is in air. A ray is incident on AB.
a. Calculate the angle of incidence at AB for which the ray strikes the diagonal face at the critical angle.
b. Assuming n=1.351, calculate the angle of incidence at AB for which the refracted rey passes through the diagonal face undeviated.

View Solution
