AB and CD are two slabs. The medium between the slabs has refractive index 2 . Find the minium angle of incidence of Q , so that the ray is totally reflected by both the slabs .
_E01_252_Q01.png)
The correct Answer is:60∘
Critical anglest at 1 and 2
_E01_252_S01.png)
θC1=sin−1(μ1μ2)=sin−1(1√2)=45∘
θC2=sin−1(μ3μ2)=sin−1(√32)=60∘
Therefore , minimum angle of incidence for total internal reflection to take place on both slabs should be 60∘
imin=60∘
Topper's Solved these Questions
Similar Questions
AB and CD are surfaces ot two slabs as shown in Figure . The medium between the slabs has refractive indes 2. Refractive indes of the slab above Ab is √2 and below CD is √3 . Find the minimum angle of incidence at Q, so that the ray is totally reflected by both the slabs.

View SolutionA rectangular slab ABCD, of refractive index n1 , is immersed in water of refractive index n2(n1<n2). A ray of light is incident at the surface AB of the slab as shown in Fig. Find the maximum value of angle of incidence αmax, such that the ray comes out only from the other surface CD.
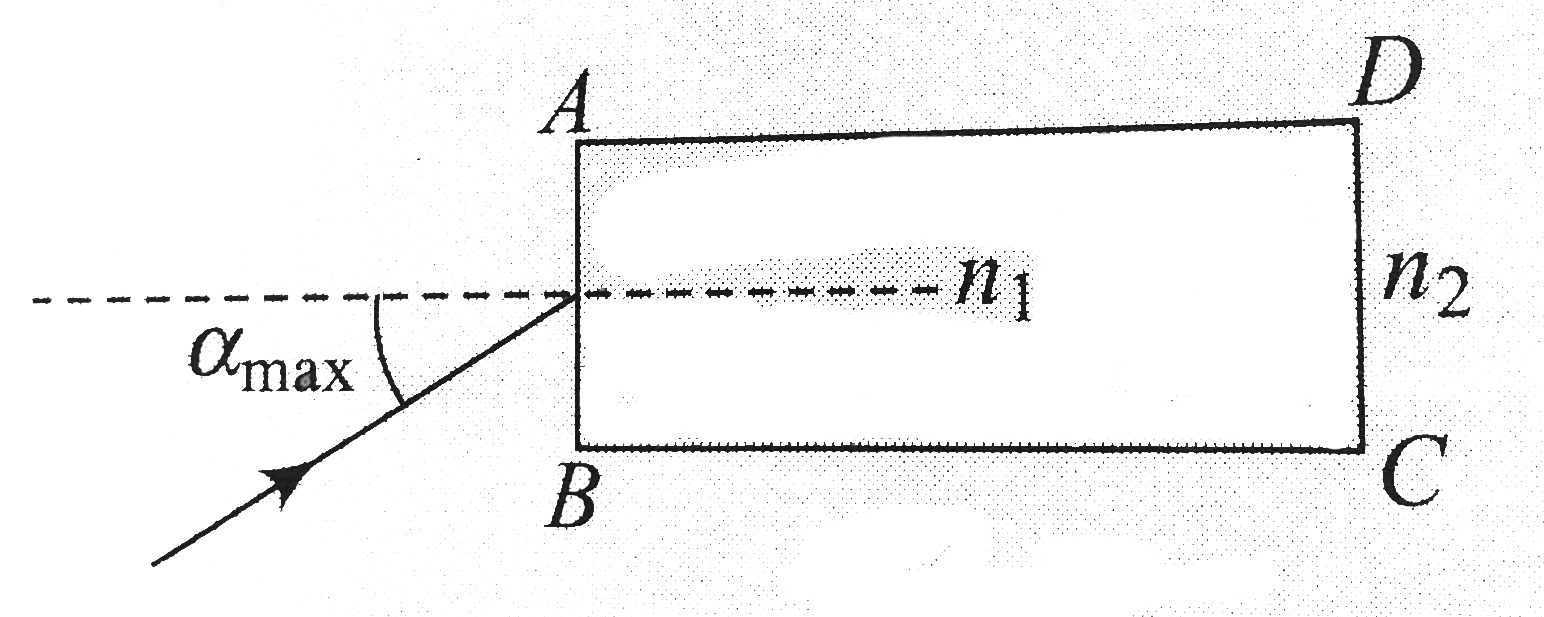
View Solution
Knowledge Check
A ray of light strikes a transparent rectangular slab of refractive index √2 at an angle of incidence of 45∘. The angle betweent the reflected and refracted rays is
A75∘B90∘C105∘D120∘
A ray of light falls on a glass plate of refractive index μ=1.5.
What is the angle of incidence of the ray if the angle between the reflected and
refracted rays is 90∘?
View SolutionA ray of light falls on a glass plate of refractive index μ=1.5.
What is the angle of incidence of the ray if the angle between the reflected and
refracted rays is 90∘?
View SolutionA ray of light is incident on a parallel slab of thickness t and refractive index n. If the angle of incidence θ is small, than the lateral displacement in the incident and emergent ray will be
View SolutionA ray of light passes from vaccum into a medium of refractive index n. If the angle of incidence is twice the angle of refraction, then the angle of incidence is
View SolutionA light ray is incident on a transparent slab of refractive index μ=√2 at an angle of incidence π/4. Find the ratio of the lateral displacement suffered by the light ray to the maximum value which it could have suffered.
View SolutionFind the distance of object placed in the slab of refractive index μ from point P of the curved surface of radius R so that image is formed at infinity:

View SolutionRefractive index of slab R if refracted ray cd is parallel to incident ray ab, is
View Solution
