A body cools in a surrounding of constant temperature 30∘C Its heat capacity is 2J/∘C. Initial temeprature of cooling is valid. The body cools to 38∘C in 10 min
The temperature of the body In .∘C denoted by θ. The veriation of θ versus time t is best denoted as


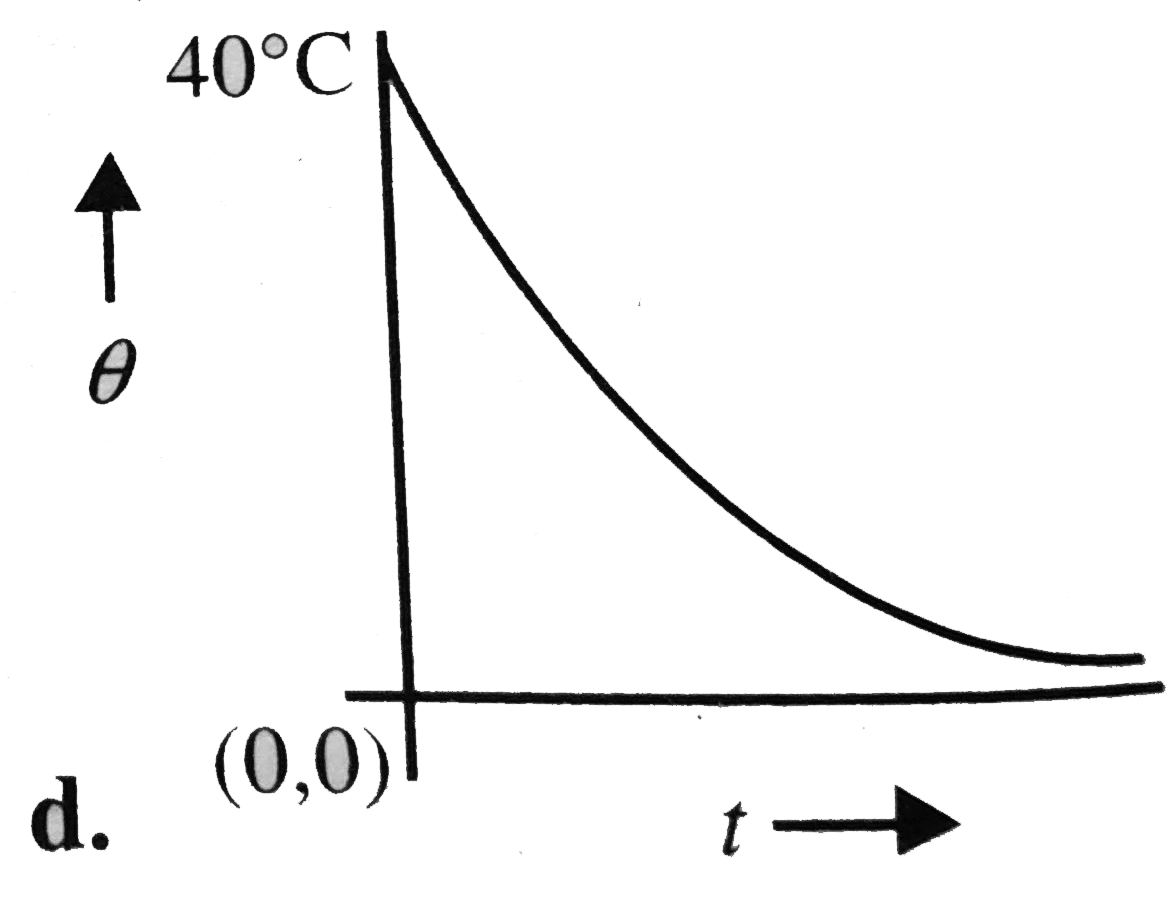
The correct Answer is:A
To solve the problem, we will use Newton's Law of Cooling, which states that the rate of change of temperature of an object is proportional to the difference between its own temperature and the ambient temperature surrounding it.
1. Identify Given Data:
- Surrounding temperature, Ts=30∘C
- Heat capacity of the body, C=2J/∘C
- Initial temperature of the body, θ1 (unknown)
- Final temperature of the body after 10 minutes, θ2=38∘C
- Time, t=10minutes=600seconds
2. Apply Newton's Law of Cooling:
According to Newton's Law of Cooling, we can express the change in temperature over time as:
dθdt=−k(θ−Ts)
where k is the cooling constant.
3. Integrate the Equation:
Rearranging gives:
dθθ−Ts=−kdt
Integrating both sides, we get:
ln|θ−Ts|=−kt+C
where C is the integration constant.
4. Solve for the Constant:
At t=0, let θ=θ1:
ln|θ1−Ts|=C
So, we have:
ln|θ−Ts|=−kt+ln|θ1−Ts|
5. Find the Cooling Constant k:
At t=600seconds, θ=38∘C:
ln|38−30|=−600k+ln|θ1−30|
Simplifying gives:
ln(8)=−600k+ln|θ1−30|
6. Relate Initial and Final Temperatures:
Rearranging gives:
ln|θ1−30|=ln(8)+600k
Thus, we can express θ1 in terms of k:
θ1=30+8e600k
7. Determine the Nature of the Graph:
The temperature θ decreases over time and approaches the surrounding temperature Ts. The graph of θ versus t will be a curve that starts at θ1 and approaches Ts asymptotically.
8. Conclusion:
The variation of θ versus t is best represented as a decreasing curve that flattens out as it approaches 30∘C.
Final Answer:
The variation of θ versus time t is best denoted by a decreasing curve that approaches 30∘C.
- Surrounding temperature, Ts=30∘C
- Heat capacity of the body, C=2J/∘C
- Initial temperature of the body, θ1 (unknown)
- Final temperature of the body after 10 minutes, θ2=38∘C
- Time, t=10minutes=600seconds
According to Newton's Law of Cooling, we can express the change in temperature over time as:
dθdt=−k(θ−Ts)
where k is the cooling constant.
Rearranging gives:
dθθ−Ts=−kdt
Integrating both sides, we get:
ln|θ−Ts|=−kt+C
where C is the integration constant.
At t=0, let θ=θ1:
ln|θ1−Ts|=C
So, we have:
ln|θ−Ts|=−kt+ln|θ1−Ts|
At t=600seconds, θ=38∘C:
ln|38−30|=−600k+ln|θ1−30|
Simplifying gives:
ln(8)=−600k+ln|θ1−30|
Rearranging gives:
ln|θ1−30|=ln(8)+600k
Thus, we can express θ1 in terms of k:
θ1=30+8e600k
The temperature θ decreases over time and approaches the surrounding temperature Ts. The graph of θ versus t will be a curve that starts at θ1 and approaches Ts asymptotically.
The variation of θ versus t is best represented as a decreasing curve that flattens out as it approaches 30∘C.
The variation of θ versus time t is best denoted by a decreasing curve that approaches 30∘C.
Topper's Solved these Questions
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Integer
8 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Multiple Correct
25 Videos
- BASIC MATHEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise 2.6
20 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE
1 Video
Similar Questions
A body cools in a surrounding of constant temperature 30∘C Its heat capacity is 2J/∘C. Initial temperature of cooling is valid. The body of mass 1 kg cools to 38∘C in 10 min
When the body temperature has reached 38∘C, it is heated again so that it reaches 40∘C in 10 min. The heat required from a heater by the body is
View SolutionA body cools in a surrounding of constant temperature 30∘C Its heat capacity is 2J/∘C. Initial temeprature of cooling is 40∘C and assuming newtons law of cooling is valid. The body cools to 38∘C in 10 min
In further 10 min it will cools from 38∘C to _____
View SolutionA body cools in a surrounding of constant temperature 30∘C. Its heat capacity is 2J/∘C. Initial temperature of the body is 40∘C. Assume Newton's law of cooling is valid. The body cools to 36∘C in 10 minutes.
In further 10 minutes it will cool from 36∘C to :
View SolutionA body having mass 2 Kg cools in a surrounding of constant temperature 30∘C. Its heat capacity is 2J/∘C. Initial temperature of the body is 40∘C. Assume Newton's law of cooling is valid. The body cools to 36∘C in 10 minutes.
When the body temperature has reached 36∘C. it is heated again so that it reaches to 40∘C in 10 minutes. Assume that the rate of loss of heat at 38∘C is the average rate of loss for the given time . The total heat required from a heater by the body is :
View SolutionA body cools from 50∘C to 40∘C in 5 min. If the temperature of the surrounding is 20∘C , the temperature of the body after the next 5 min would be
View SolutionA body at temperature 40∘C is kept in a surrounding of constant temperature 20∘C. It is observed that its temperature falls to 35∘C in 10 minutes. Find how much more time will it taken for the body to attain a temperature of 30∘C.
View SolutionA body takes 10 min to cool douwn from 62∘C to 50∘C. If the temperature of surrounding is 26∘C then in the next 10 minutes temperature of the body will be
View SolutionA body cools from 50∘C to 40∘C in 5 mintues in surrounding temperature 20∘C. Find temperature of body in next 5 mintues.
View SolutionA body is heated to a temperature 40∘C and kept in a chamber maintained at 20∘C. If the temperature of the body decreases to 36∘C in 2 minutues, then the time after which the temperature will further decrease by 4∘C, is
View SolutionA body cools in 7 min from 60∘C to 40∘C What will be its temperature after the next 7 min? The temperature of surroundings is 10∘C.
View Solution

