Two circles with centres O and O' of radii 3 cm and 4 cm, respectively intersect at two points P and Q such that OP and O'P are tangents to the two circles. Find the length of common chord PQ.
To find the length of the common chord PQ of two intersecting circles with centers O and O′ and radii 3 cm and 4 cm respectively, we can follow these steps:
Step 1: Identify the given values
- Radius of circle with center O (denote as r1) = 3 cm
- Radius of circle with center O′ (denote as r2) = 4 cm
Step 2: Use the Pythagorean theorem
Since OP and O′P are tangents to the circles at point P, we can apply the Pythagorean theorem to triangle OO′P.
Let OO′=d (the distance between the centers of the circles).
Using the Pythagorean theorem:
OO′2=OP2+O′P2
Substituting the values:
d2=(4 cm)2+(3 cm)2
d2=16+9=25
d=√25=5 cm
Step 3: Find the length of the perpendicular from the center to the chord
Let M be the midpoint of the chord PQ. The length of OM can be found using the cosine of the angle θ where cosθ=OPOO′.
Using the cosine relation:
cosθ=45
Step 4: Find PM using sine
Using the sine relation in triangle OMP:
sinθ=PMOP
We can express PM as:
PM=OP⋅sinθ
Using sin2θ+cos2θ=1:
sin2θ=1−(45)2=1−1625=925
sinθ=35
Thus,
PM=4⋅35=125 cm
Step 5: Find the length of the common chord PQ
Since PQ=2⋅PM:
PQ=2⋅125=245 cm
Final Answer
The length of the common chord PQ is 245 cm or 4.8 cm.
---
- Radius of circle with center O (denote as r1) = 3 cm
- Radius of circle with center O′ (denote as r2) = 4 cm
Since OP and O′P are tangents to the circles at point P, we can apply the Pythagorean theorem to triangle OO′P.
OO′2=OP2+O′P2
Substituting the values:
d2=(4 cm)2+(3 cm)2
d2=16+9=25
d=√25=5 cm
Let M be the midpoint of the chord PQ. The length of OM can be found using the cosine of the angle θ where cosθ=OPOO′.
cosθ=45
Using the sine relation in triangle OMP:
sinθ=PMOP
We can express PM as:
PM=OP⋅sinθ
Using sin2θ+cos2θ=1:
sin2θ=1−(45)2=1−1625=925
sinθ=35
Thus,
PM=4⋅35=125 cm
Since PQ=2⋅PM:
PQ=2⋅125=245 cm
The length of the common chord PQ is 245 cm or 4.8 cm.
Topper's Solved these Questions
- CIRCLESBook:NAGEEN PRAKASHAN ENGLISHChapter:CIRCLESExercise:Exercise
Explore 32 Videos
- CIRCLESBook:NAGEEN PRAKASHAN ENGLISHChapter:CIRCLESExercise:Revision Exercise Very Short Answer Question
Explore 7 Videos
- CIRCLESBook:NAGEEN PRAKASHAN ENGLISHChapter:CIRCLESExercise:Long Answer Questions
Explore 2 Videos
- ARITHMETIC PROGRESSIONBook:NAGEEN PRAKASHAN ENGLISHChapter:ARITHMETIC PROGRESSIONExercise:Revision Exercise Long Answer Question
Explore 5 Videos
- CO-ORDINATE GEOMETRYBook:NAGEEN PRAKASHAN ENGLISHChapter:CO-ORDINATE GEOMETRYExercise:Revision Exercise Short Answer Questions
Explore 10 Videos
Similar Questions
Two circles with centers O and O' of radii 6cm and 8 cm respectively intersect two points P and Q such that OP and O'P are tangents to the two circle. The length of the common chord PQ is
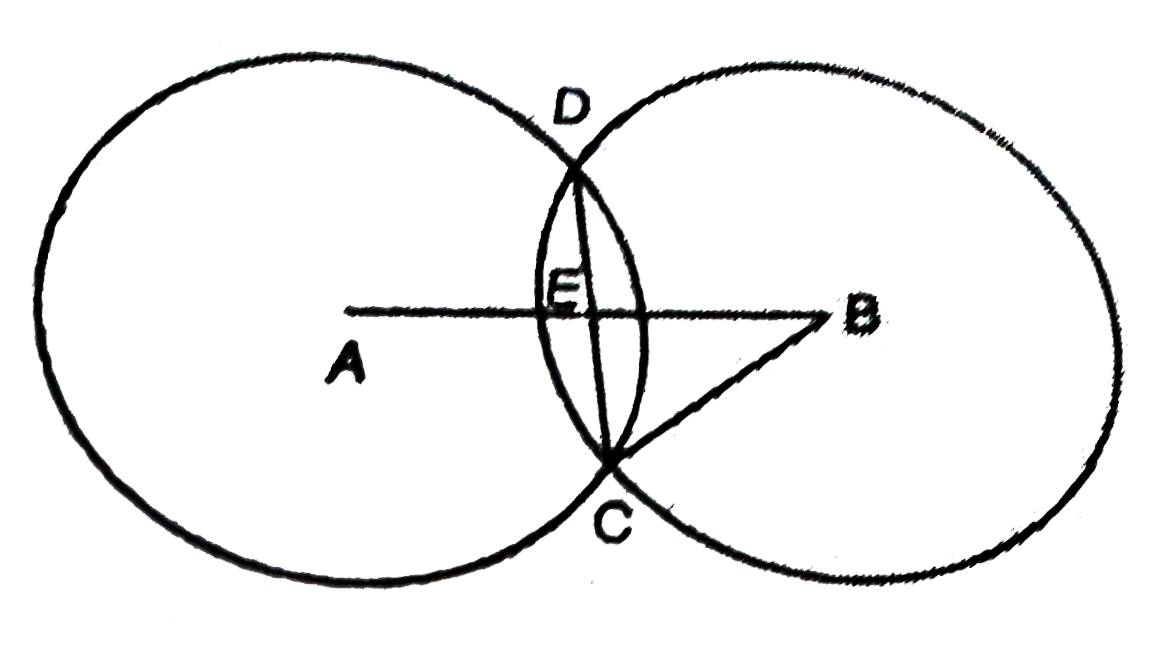
View SolutionTwo circles with centres AandB of radii 3cmand4cm respectively intersect at two points CandD such that ACandBC are tangents to the two circles. Find the length of the common chord CD.
View SolutionTwo circles of radii 10 cm and 17 cm . Intersecting each other at two points and the distances between their centres is 21 cm . Find the length of the common chords.
View SolutionIn Figure, there are two concentric circles with centre O of radii 5cmand3cm . From an external point P, tangents PAandPB are drawn to these circles. If AP=12cm, find the length of BP.
View SolutionTwo circles of radii 5 cm and 3cm intersect at two points and the distance between their centres is 4cm. Find the length of the common chord.
View SolutionTwo circles of radii 5 cm and 3cm intersect at two points and the distance between their centres is 4cm. Find the length of the common chord.
View SolutionAP is tangent to circle O at point P, What is the length of OP?
View SolutionIn the figure, two circles with centres AandB and of radii 5cmand3cm touch each other intermally. If the perpendicular bisectors of segment AB meets the bigger circle in PandQ. Find the length of PQ.
View SolutionTwo circles with centres A and B and radii 5 cm and 3 cm, touch each other internally. If the perpendicular bisector of the segment AB meets the bigger circle in P and Q, find the length of PQ.
View SolutionIn the adjoining figure, A and B are the centres of two circles. If CB=17cm, EB=15cm, then find the length of common chord.
View Solution

