Two circles with centers O and O' of radii 6cm and 8 cm respectively intersect two points P and Q such that OP and O'P are tangents to the two circle. The length of the common chord PQ is
To find the length of the common chord PQ of two intersecting circles with centers O and O' and radii 6 cm and 8 cm respectively, we can follow these steps:
1. Draw the Circles and Identify Points:
- Draw two circles with centers O and O' such that the radius of circle O is 6 cm and the radius of circle O' is 8 cm.
- Let the points of intersection of the two circles be P and Q.
2. Identify Tangents:
- Since OP and O'P are tangents to the circles, we know that the angle between the radius and the tangent at the point of contact is 90 degrees.
- Therefore, ∠O'PO = 90°.
3. Apply the Pythagorean Theorem:
- In triangle OPO', we can apply the Pythagorean theorem:
OO′2=OP2+O′P2
- Here, OP = 6 cm and O'P = 8 cm.
- Therefore:
OO′2=62+82=36+64=100
- Taking the square root gives us:
OO′=√100=10 cm
4. Draw a Perpendicular from O to PQ:
- Draw a perpendicular line from point O to the chord PQ, meeting PQ at point N.
- This creates two right triangles: OPN and O'PN.
5. Use the Pythagorean Theorem in Triangle OPN:
- In triangle OPN, we can apply the Pythagorean theorem:
OP2=ON2+PN2
- Let ON = x cm. Then:
62=x2+PN2(1)
6. Use the Pythagorean Theorem in Triangle O'PN:
- In triangle O'PN, we can apply the Pythagorean theorem:
O′P2=O′N2+PN2
- Since O'N = OO' - ON = 10 - x, we have:
82=(10−x)2+PN2(2)
7. Set Up the Equations:
- From equation (1):
PN2=36−x2
- From equation (2):
PN2=64−(10−x)2
8. Equate and Simplify:
- Set the two expressions for PN² equal to each other:
36−x2=64−(100−20x+x2)
- Simplifying gives:
36−x2=64−100+20x−x2
36=−36+20x
72=20x
x=7220=185 cm
9. Find PN:
- Substitute x back into equation (1):
PN2=36−(185)2
PN2=36−32425=900−32425=57625
PN=245 cm
10. Calculate the Length of Chord PQ:
- Since N is the midpoint of PQ, the length of PQ is:
PQ=2×PN=2×245=485 cm
Final Answer:
The length of the common chord PQ is 485 cm or 9.6 cm.
- Draw two circles with centers O and O' such that the radius of circle O is 6 cm and the radius of circle O' is 8 cm.
- Let the points of intersection of the two circles be P and Q.
- Since OP and O'P are tangents to the circles, we know that the angle between the radius and the tangent at the point of contact is 90 degrees.
- Therefore, ∠O'PO = 90°.
- In triangle OPO', we can apply the Pythagorean theorem:
OO′2=OP2+O′P2
- Here, OP = 6 cm and O'P = 8 cm.
- Therefore:
OO′2=62+82=36+64=100
- Taking the square root gives us:
OO′=√100=10 cm
- Draw a perpendicular line from point O to the chord PQ, meeting PQ at point N.
- This creates two right triangles: OPN and O'PN.
- In triangle OPN, we can apply the Pythagorean theorem:
OP2=ON2+PN2
- Let ON = x cm. Then:
62=x2+PN2(1)
- In triangle O'PN, we can apply the Pythagorean theorem:
O′P2=O′N2+PN2
- Since O'N = OO' - ON = 10 - x, we have:
82=(10−x)2+PN2(2)
- From equation (1):
PN2=36−x2
- From equation (2):
PN2=64−(10−x)2
- Set the two expressions for PN² equal to each other:
36−x2=64−(100−20x+x2)
- Simplifying gives:
36−x2=64−100+20x−x2
36=−36+20x
72=20x
x=7220=185 cm
- Substitute x back into equation (1):
PN2=36−(185)2
PN2=36−32425=900−32425=57625
PN=245 cm
- Since N is the midpoint of PQ, the length of PQ is:
PQ=2×PN=2×245=485 cm
The length of the common chord PQ is 485 cm or 9.6 cm.
Topper's Solved these Questions
- CIRCLESBook:NCERT EXEMPLAR ENGLISHChapter:CIRCLESExercise:EXERCISE 9.3 SHORT ANSWER TYPE QUESTIONS
Explore 10 Videos
- ARITHMETIC PROGRESSIONSBook:NCERT EXEMPLAR ENGLISHChapter:ARITHMETIC PROGRESSIONSExercise:Long Answer Type Questions
Explore 10 Videos
- CONSTRUCTIONSBook:NCERT EXEMPLAR ENGLISHChapter:CONSTRUCTIONSExercise:Exercise 10.4 Long Answer type Questions
Explore 7 Videos
Similar Questions
Two circles with centres O and O' of radii 3 cm and 4 cm, respectively intersect at two points P and Q such that OP and O'P are tangents to the two circles. Find the length of common chord PQ.
View SolutionTwo circles of radii 10 cm and 17 cm . Intersecting each other at two points and the distances between their centres is 21 cm . Find the length of the common chords.
View SolutionIn Figure, there are two concentric circles with centre O of radii 5cmand3cm . From an external point P, tangents PAandPB are drawn to these circles. If AP=12cm, find the length of BP.
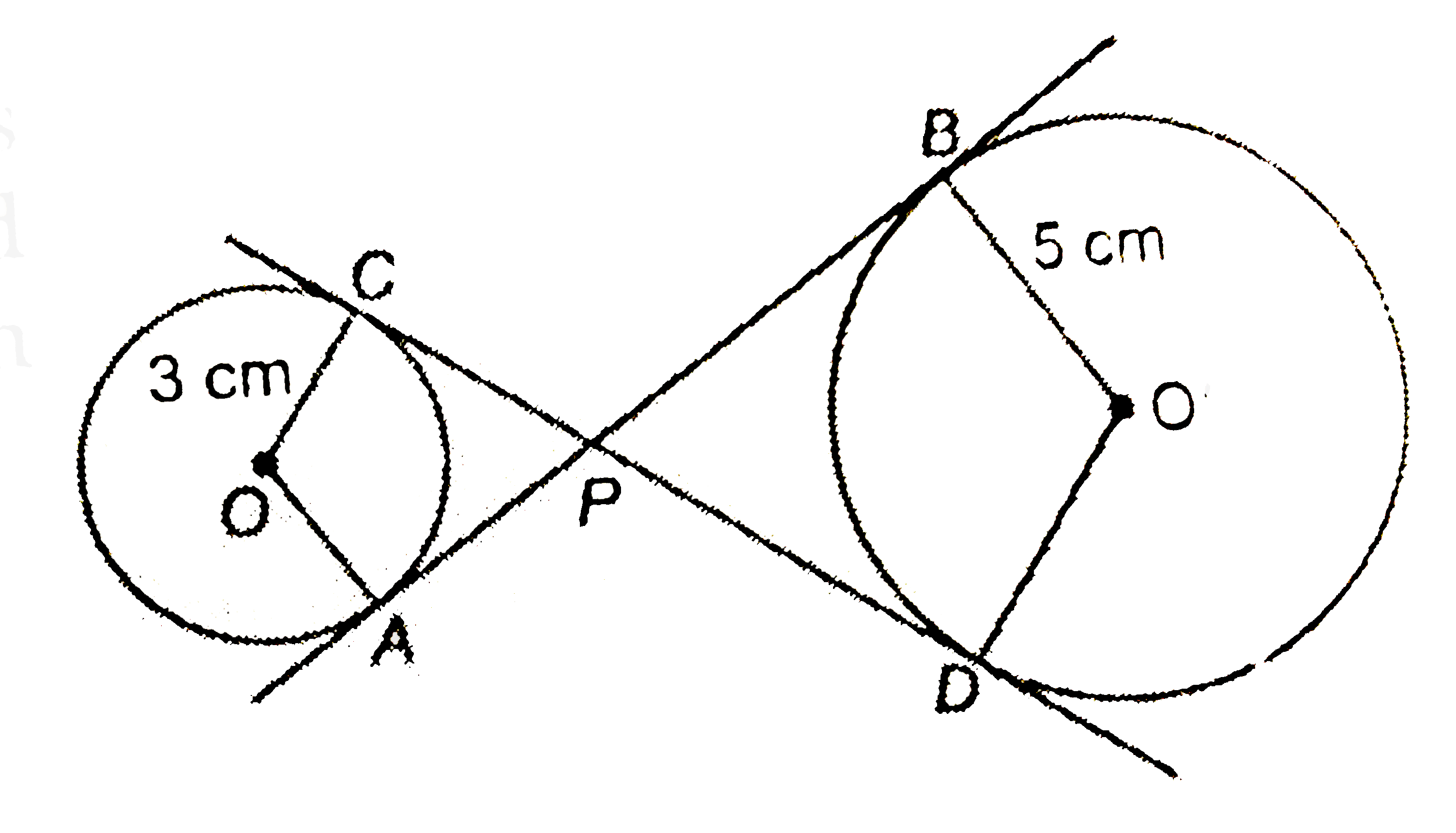
View SolutionIn figure, CPD and APB are common tangents to the two circles with centres O and O'. The radii of the two circles are 3 cm and 5 cm respectively. If AP:PB=1:3 and CP=4cm. Find the length of PB and OO'.
View SolutionIn the given figure two concentric circles with centre O are of radii 5 cm and 3 cm. From an external point P, tangents PA and PB are drawn to these circles. If AP =12 cm find BP.

View SolutionTwo circles with centres A and B intersect each other at points P and Q. Prove that the centre-line AB bisects the common chord PQ perpendicularly.
View SolutionThe radii of two circles are 8 cm and 6 cm respectively. Find the radius of the circle having area equal to the sum of the areas of the two circles.
View SolutionThe radii of two circles are 8 cm and 6 cm respectively. Find the radius of the circle having its area equal to the sum of the areas of the two circles.
View SolutionIn the figure, two circles with centres AandB and of radii 5cmand3cm touch each other intermally. If the perpendicular bisectors of segment AB meets the bigger circle in PandQ. Find the length of PQ.
View SolutionIf the angle of intersection at a point where the two circles with radii 5 cm and 12 cm intersect is 90∘, then the length (in cm) of their common chord is
View Solution

