The tangent at a point C of a circle and a diameter AB when extended intersect at P. If ∠PCA=110∘find∠CBA.
20∘
70∘
60∘
80∘
The correct Answer is:B
To solve the problem, we will follow these steps:
Step 1: Draw the Circle and Label the Points
- Draw a circle with center O.
- Draw the diameter AB of the circle.
- Extend the diameter AB to point P.
- Mark point C on the circumference of the circle such that line CP is tangent to the circle at point C.
Step 2: Identify the Given Angle
- We are given that ∠PCA=110∘.
Step 3: Use Properties of the Circle
- Since AB is a diameter, by the property of a circle, we know that ∠BCA=90∘ (the angle inscribed in a semicircle is a right angle).
- Also, the tangent at point C is perpendicular to the radius OC at point C, so ∠PCO=90∘.
Step 4: Relate the Angles
- We can express ∠PCA in terms of ∠PCO and ∠OCA:
∠PCA=∠PCO+∠OCA
- Substituting the known values:
110∘=90∘+∠OCA
- Solve for ∠OCA:
∠OCA=110∘−90∘=20∘
Step 5: Use Isosceles Triangle Property
- In triangle OCA, since OC = OA (both are radii of the circle), triangle OCA is isosceles.
- Therefore, the angles opposite the equal sides are equal:
∠OCA=∠OAC=20∘
Step 6: Find the Remaining Angle in Triangle ABC
- Now, consider triangle ABC. The sum of the angles in a triangle is 180∘:
∠CAB+∠BCA+∠CBA=180∘
- We know:
- ∠CAB=∠OCA=20∘
- ∠BCA=90∘
- Substitute these values into the equation:
20∘+90∘+∠CBA=180∘
- Simplifying gives:
110∘+∠CBA=180∘
- Solve for ∠CBA:
∠CBA=180∘−110∘=70∘
Final Answer
Thus, the value of ∠CBA is 70∘.
---
- Draw a circle with center O.
- Draw the diameter AB of the circle.
- Extend the diameter AB to point P.
- Mark point C on the circumference of the circle such that line CP is tangent to the circle at point C.
- We are given that ∠PCA=110∘.
- Since AB is a diameter, by the property of a circle, we know that ∠BCA=90∘ (the angle inscribed in a semicircle is a right angle).
- Also, the tangent at point C is perpendicular to the radius OC at point C, so ∠PCO=90∘.
- We can express ∠PCA in terms of ∠PCO and ∠OCA:
∠PCA=∠PCO+∠OCA
- Substituting the known values:
110∘=90∘+∠OCA
- Solve for ∠OCA:
∠OCA=110∘−90∘=20∘
- In triangle OCA, since OC = OA (both are radii of the circle), triangle OCA is isosceles.
- Therefore, the angles opposite the equal sides are equal:
∠OCA=∠OAC=20∘
- Now, consider triangle ABC. The sum of the angles in a triangle is 180∘:
∠CAB+∠BCA+∠CBA=180∘
- We know:
- ∠CAB=∠OCA=20∘
- ∠BCA=90∘
- Substitute these values into the equation:
20∘+90∘+∠CBA=180∘
- Simplifying gives:
110∘+∠CBA=180∘
- Solve for ∠CBA:
∠CBA=180∘−110∘=70∘
Thus, the value of ∠CBA is 70∘.
Topper's Solved these Questions
- CIRCLESBook:NCERT EXEMPLAR ENGLISHChapter:CIRCLESExercise:EXERCISE 9.3 SHORT ANSWER TYPE QUESTIONS
Explore 10 Videos
- ARITHMETIC PROGRESSIONSBook:NCERT EXEMPLAR ENGLISHChapter:ARITHMETIC PROGRESSIONSExercise:Long Answer Type Questions
Explore 10 Videos
- CONSTRUCTIONSBook:NCERT EXEMPLAR ENGLISHChapter:CONSTRUCTIONSExercise:Exercise 10.4 Long Answer type Questions
Explore 7 Videos
Similar Questions
In the adjoinig figure, AB is a diameter of the circle, CD is a chord equal to the radius of the circle. AC and BD when extended intersect at a point E. Prove that ∠AEB=60∘.

View SolutionIn the given figure, AB is diameter of a circle with centre O and AT is a tangent at ∠AOQ=58∘, find ∠ATQ.
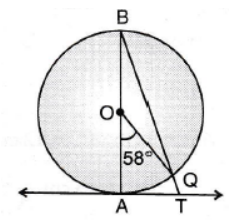
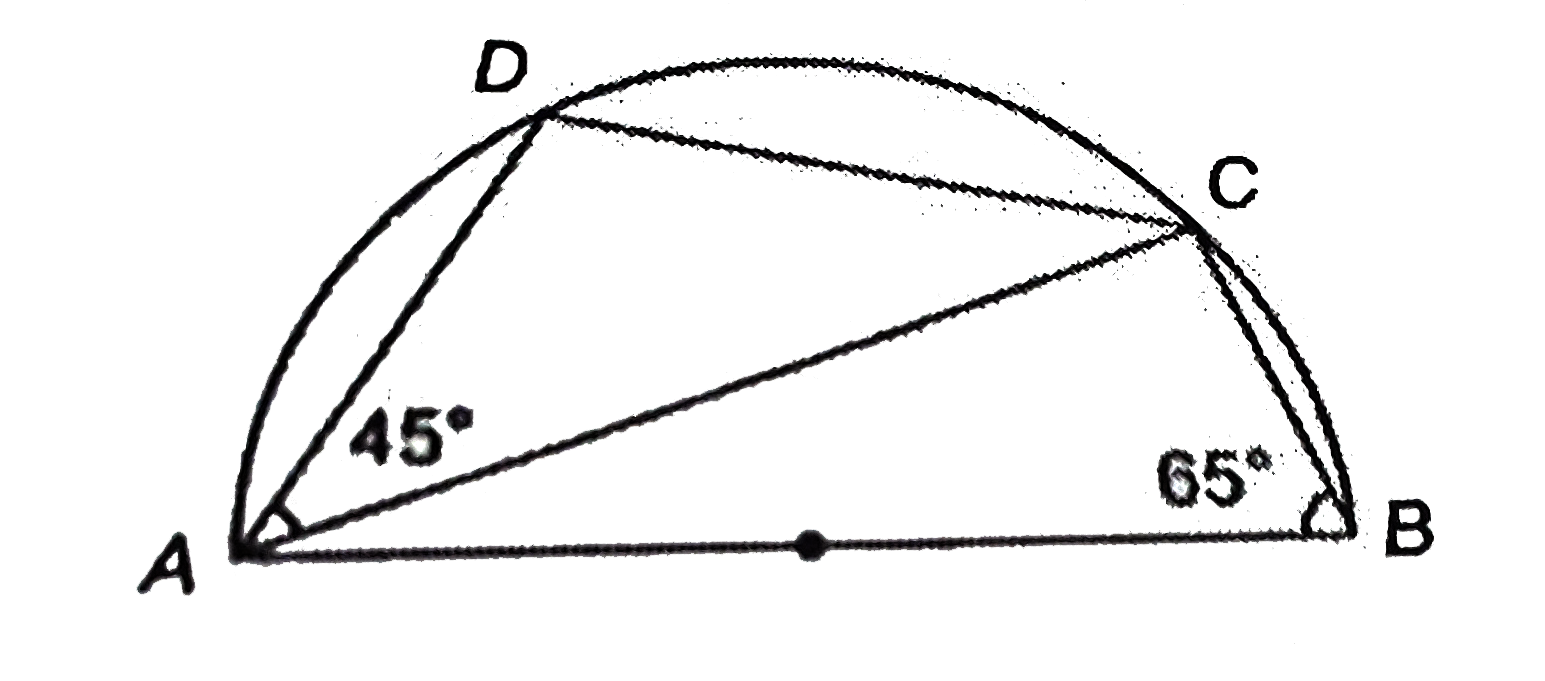
View SolutionIn the adjoining figure, AB is the diameter of the circle and two points C and D are on the circle. If ∠CAD=45∘ and ∠ABC=65∘, then find the value of ∠DCA.
View SolutionIn the given figure, PA and PB are tangents to a circle from an external point P such that PA=4 cm and ∠BAC=135∘. Find the length of dhord AB.

View SolutionIn Figure, AB is a diameter of the circle, CD is a chord equal to the radius of the circle. AC and BD when extended intersect at a point E. Prove that ∠AEB=60∘
View SolutionShow that tangent lines at the end points of a diameter of a circle are parallel.
View SolutionFrom an external point P, tangents PA and PB are drawn to a circle. CE is a tangent to the circle at D which intersect PA and PB at point E and C respectvely. If AP=15 cm, find the permeter of the △PEC.
View SolutionIn figure, AB is a chord of the circle and AOC is the diameter such that ∠ACB=50∘. If AT is the tangent to the circle at the point A, then angleBAT is equal to : (a) 45∘ , (b) 60∘ , (c) 50∘ , (d) 55∘
View SolutionIn the given AB is a diameter and DC is tangent which meets AB produced at point. C . If ∠DAC=x∘, find in terms of x∘:
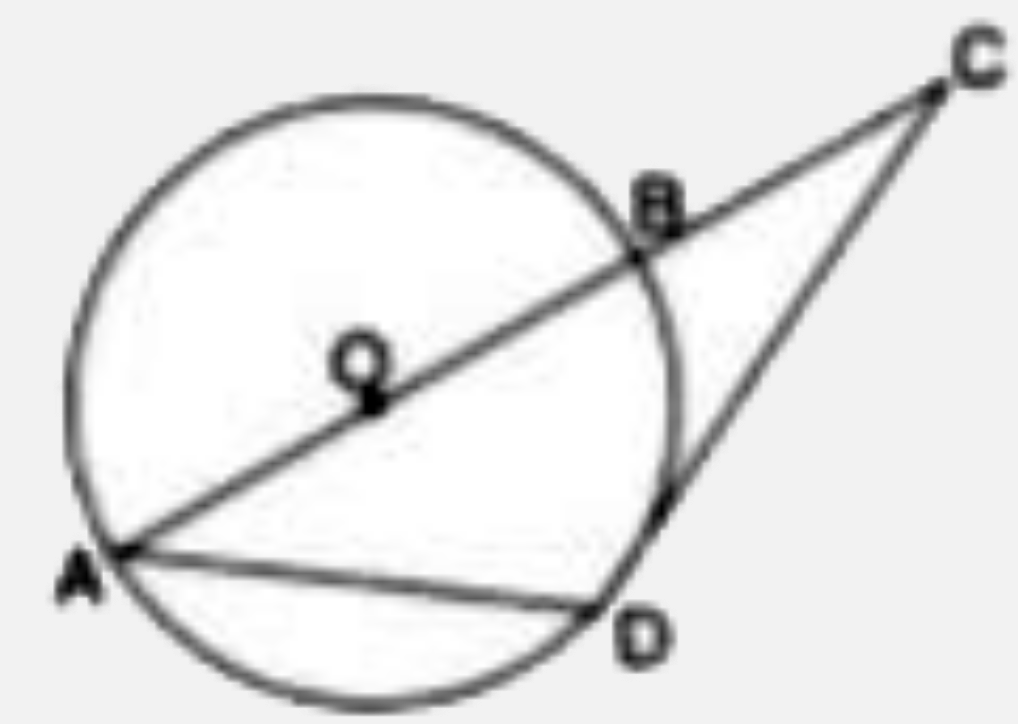
∠DCB
View SolutionIn the given AB is a diameter and DC is tangent which meets AB produced at point. C . If ∠DAC=x∘, find in terms of x∘:

∠DBC
View Solution

