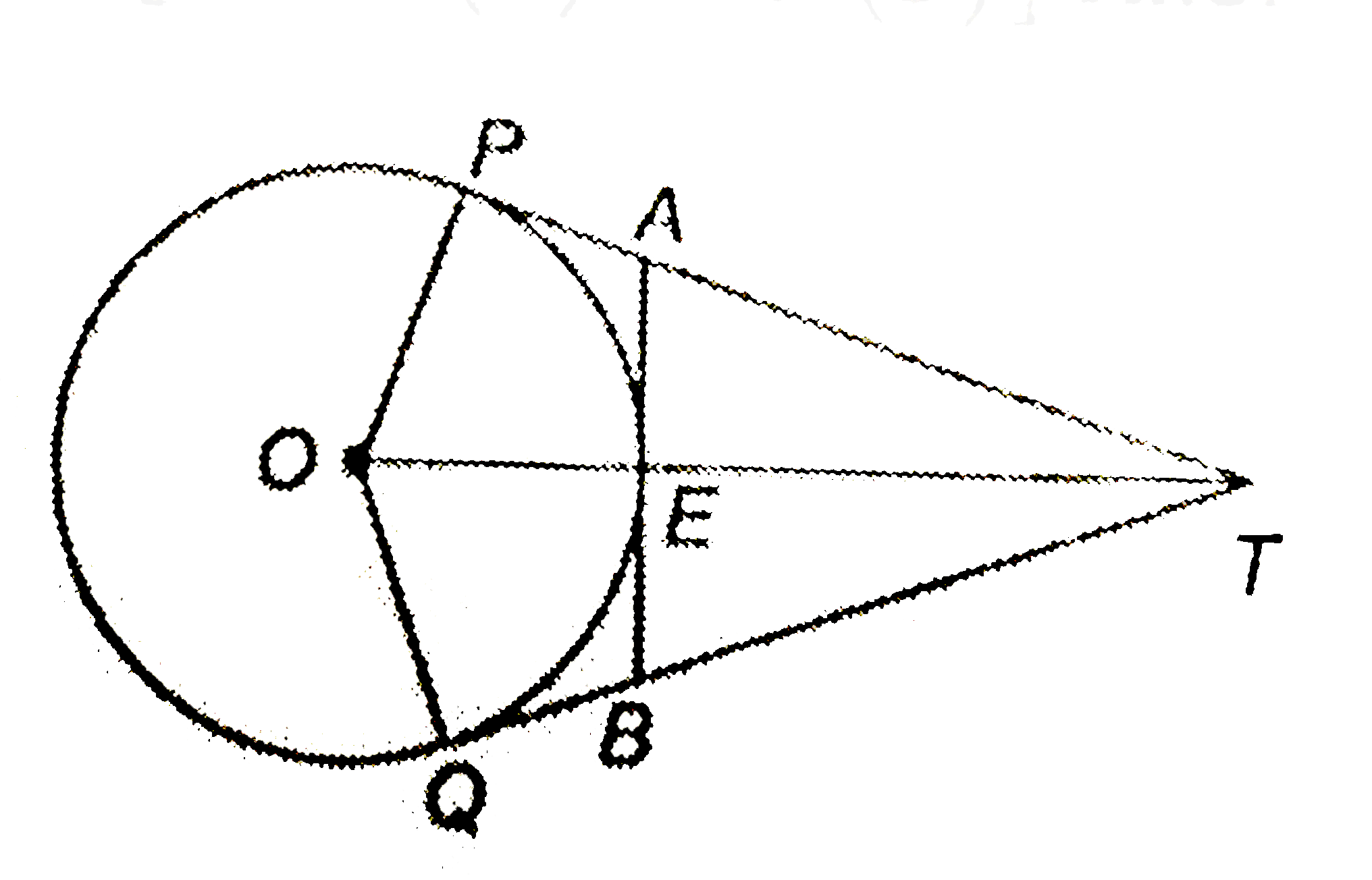
Type V: O is the center of the circle of radius 5cm. T is a point such that OT=13cm and OT intersects the circle at E . If AB is the tangent to the circle at E; find the length of AB.

Video Solution

Text Solution

Verified by Experts

Given, OT =13cm and OP =5cm
Since, if we drawn a line from the centre to the tangent of the circle. It is always perpendicular to the tangent i.e., $O P ⊥ P T .$
In right angled $Δ O P T, O T^{2} = O P^{2} + P T^{2}$
[by Pythagoras theorem, ${(hypotenuse)}^{2} = {(base)}^{2} + {(perpendicular)}^{2}$ ]
$\Rightarrow P T^{2} = {(13)}^{2} - {(5)}^{2} = 169 - 25 = 144$
$\Rightarrow P T = 12 c m$
Since, the langth of pair of tangents from an external point T is equal.
$∴ Q T = 12 c m$
Now, TA=PT-PA
$\Rightarrow T A = 12 - P A ... . . (i)$
and TB=QT-QB
$\Rightarrow T B = 12 - Q B ... ... (i i)$
Again using the property, length of pair of tanagets from an external point is equal.
$∴ P A = A E and Q B = E B ... ... . (i i i)$
$∴ O T = 13 c m$
$∴ E T = O T - O E [∴ O E = 5 c m = radius]$
$\Rightarrow E T = 13 - 5$
$\Rightarrow E T = 8 c m$
Since, AB is a tangent and OE is the radius.
$∴ O E ⊥ A B$
$\Rightarrow ∠ O E A = 90^{\circ}$
$∴ ∠ A E T = 180^{\circ} - ∠ O E A$ [linear pair]
$\Rightarrow ∠ A E T = 90^{\circ}$
Now, in right angled $Δ A E T$ ,
${(A T)}^{2} = {(A E)}^{2} + {(E T)}^{2}$ [by Pythagoras theorem]
$\Rightarrow {(P T - P A)}^{2} = {(A E)}^{2} + {(8)}^{2}$
$\Rightarrow {(12 - P A)}^{2} = {(A P)}^{2} + {(8)}^{2}$ [from Eq. (iii)]
$\Rightarrow 144 + {(P A)}^{2} - 24 . P A = {(P A)}^{2} + 64$
$\Rightarrow 24 . P A = 80$
$\Rightarrow P A = \frac{10}{3} c m$
$∴ A E = \frac{10}{3} c m$ [from Eq. (iii)]
Join OQ.
Similarly $B E = \frac{10}{3} c m$
Hence, $A B = A E + E B$
$= \frac{10}{3} + \frac{10}{3}$
$= \frac{20}{3} c m$
Hence, the required length AB is $= \frac{20}{3} c m$ .

Updated on:21/07/2023

|

Class 10 MATHS CIRCLES

Topper's Solved these Questions

Similar Questions

NCERT EXEMPLAR ENGLISH-CIRCLES-EXERCISE 9.4 LONG ANSWER TYPE QUESTIONS

Home
Ask Doubt
Profile