Question

In a right angle triangle $\Delta ABC$ is which $\angle B={90}^{\circ }$ a circle is drawn with AB diameter intersecting the hypotenuse AC at P.Prove that the tangent to the circle at PQ bisects BC.

Explanation

Let O be the centre of the given circle. Suppose, the tangent at P meets BC at Q. Join BP.

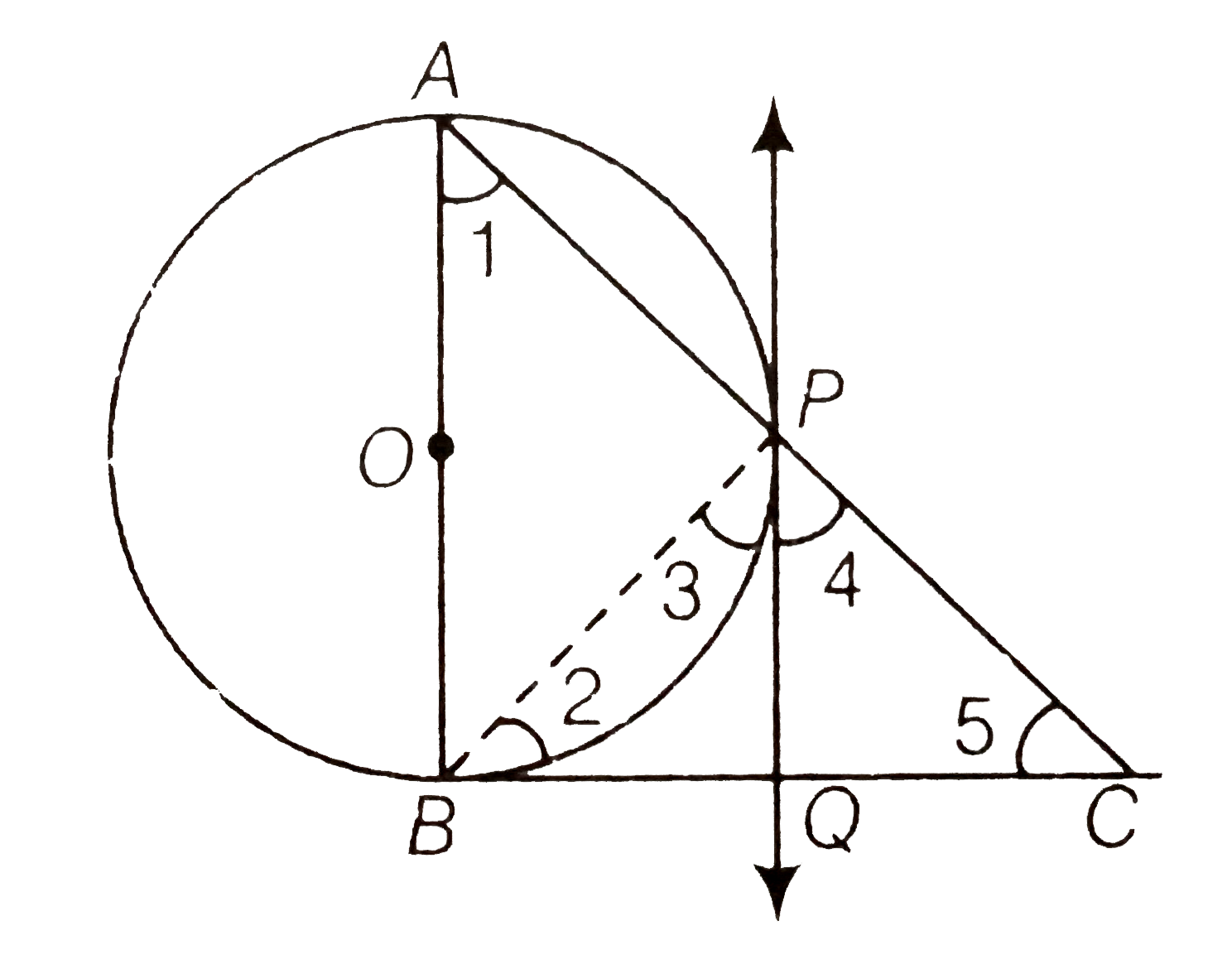
To prove BQ=QC [angles in alternate segment]
Proof `angleABC=90^(@)`
[tangent at any point of circle is perpendicular to radius through the point of contact] :.In `DeltaABC`, `angle1+angle5=90^(@)` [angle sum property, [`angleABC=90^(@)`]
`angle3=angle1`
[angle between tangent and the chord equals angle made by the chord in alternate segment]
`:.angle3+angle5=90^(@).....(i)`
Also, `:.angleAPB=90^(@)` [angle in semi-circle]
`rArrangle3+angle4=90^(@)` `[angleAPB+angleBPC=180^(@),"linera pair"]`
From Eqs. (i) and (ii), we get
`angle3+angle5+angle3+angle4`
`rArrangle5=angle4`
`rArrPQ=QC` [sides opposite to equal angles are equal]
Also, QP=QB
[tangents drawn from an internal point to a circle are equal]
`rArrQB=QC` Hence proved.