If a hexagon ABCDEF circumscribe a circle, prove that
Given A hexagon ABCDEF circumscirbe a circle.
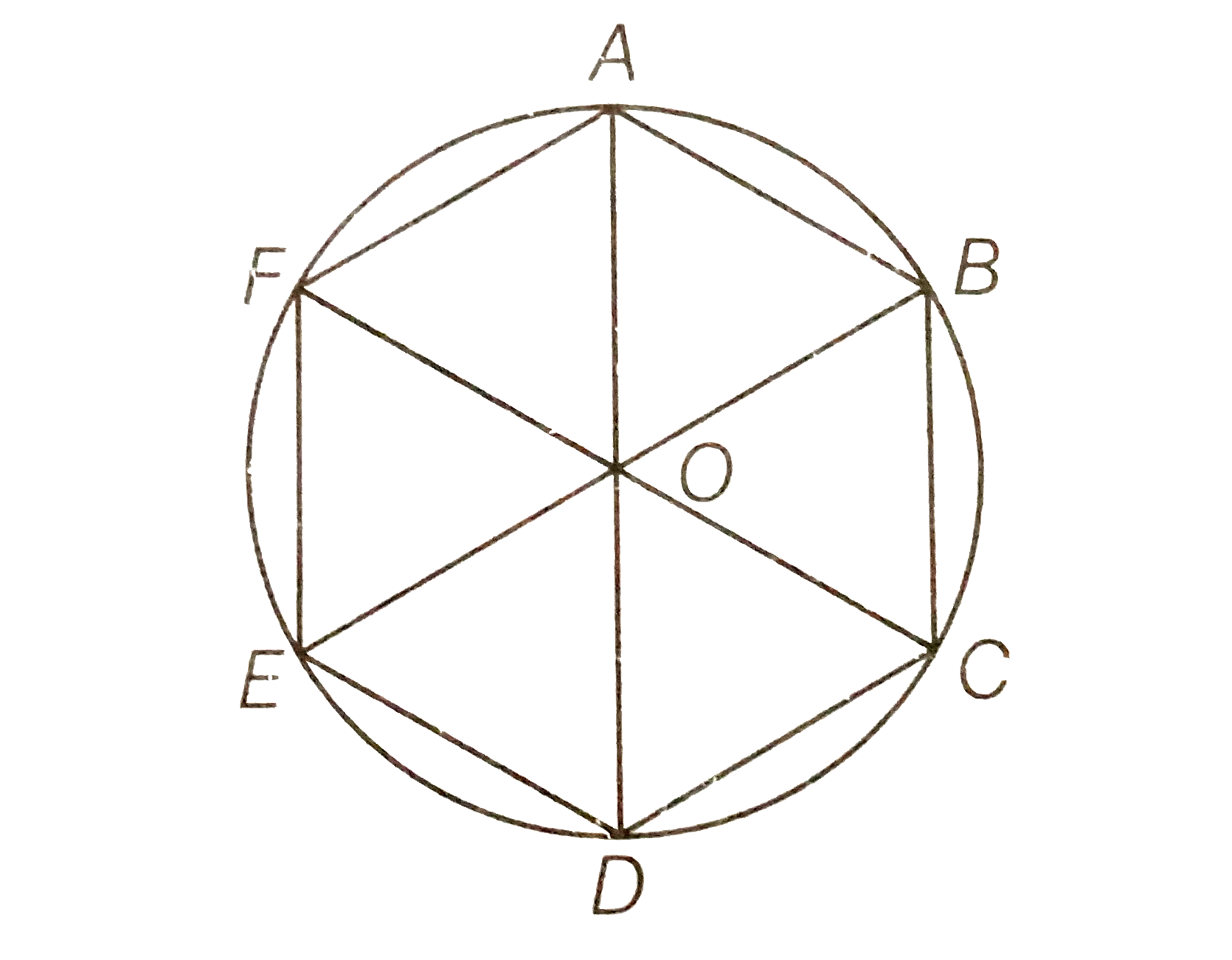
To prove
Proof
:.AQ=AP
QB=BR
CS=CR
DS=DT
EU=ET
[tangents drawn from an external point to a circle are equal]
Hence proved.
Related Playlists
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - EXERCISE 9.3 SHORT ANSWER TYPE QUESTIONS10videos
CIRCLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ARITHMETIC PROGRESSIONSEXERCISE - Long Answer Type Questions10videos
ARITHMETIC PROGRESSIONS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - Exercise 10.4 Long Answer type Questions7videos
CONSTRUCTIONS
Similar Questions
In a hexagon ABCDEF circumscribe a circle, prove that AB+CD+EF=BC+DE+FA.
View SolutionIn Figure, a quadrilateral ABCD is drawn to circumscribe a circle .
Prove that
AB+CD=BC+AD
 View Solution
View SolutionIn Figure, a quadrilateral ABCD is drawn to circumscribe a circle .
Prove that
AB+CD=BC+AD
 View Solution
View SolutionA quadrilateral ABCD is drawn to circumscribe a circle. Prove that AB+CD=AD+BC.
or
A circle touches all the four sides of a quadrilateral ABCD. Prove that AB+CD=BC+DA.View SolutionIf ABCDEF is a regular hexagon, prove that AD+EB+FC=4AB.
View SolutionIf the sides of a quadrilateral ABCD touch a circle prove that
AB+CD=BC+AD.View SolutionIf a parallelogram circumscribes a circle then prove that it must be a rhombus.
 View Solution
View SolutionIn figure ΔABC is circumscribing a circle. Find the length of BC
View Solution△ABC is an isosceles triangle in which AB=AC, circumscribed about a circle. Prove that the base is bisccted by the point of contact.
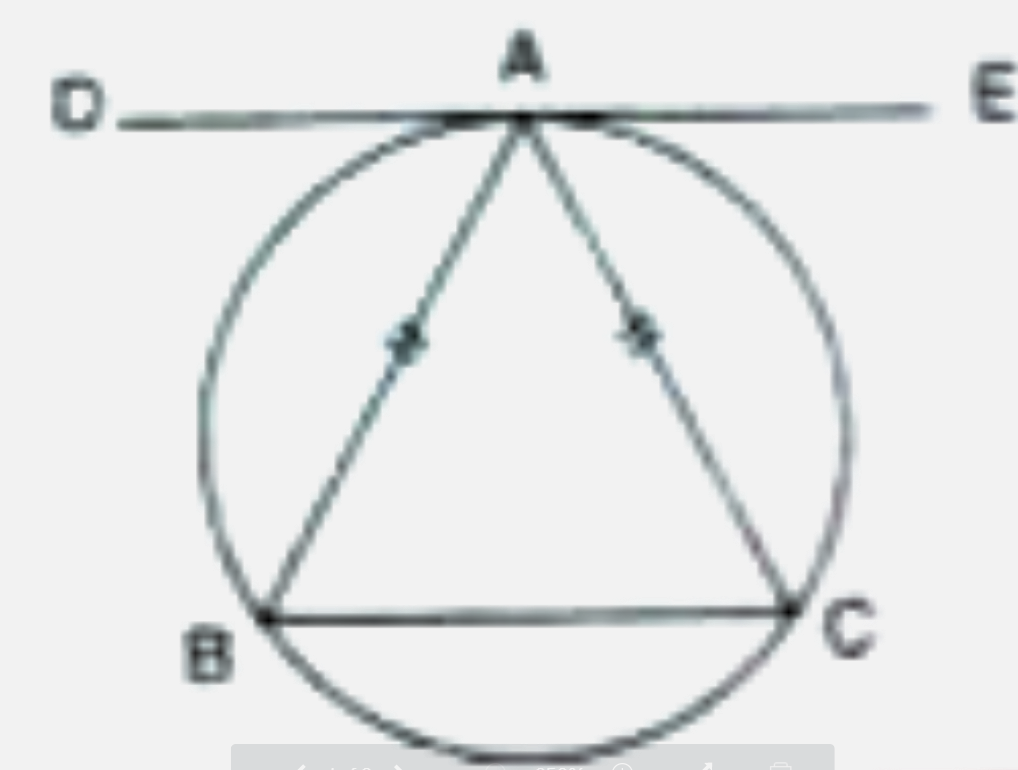
View SolutionThe given figure shows an isosceles triangle ABC inscribed in a circle such that AB=AC. If DAE is a tangent to the circle at point A, prove that DE is parallel to BC.
 View Solution
View Solution


