AP is tangent to circle O at point P, What is the length of OP?
Let the radius of given circle is r.
∴ OP=OB=r
∴ OA=2+r, OP=r, AP=4
∴ OP=OB=r
∴ OA=2+r, OP=r, AP=4
∠OPA=90∘ (radius through point of contact is perpendicular to the tangent)
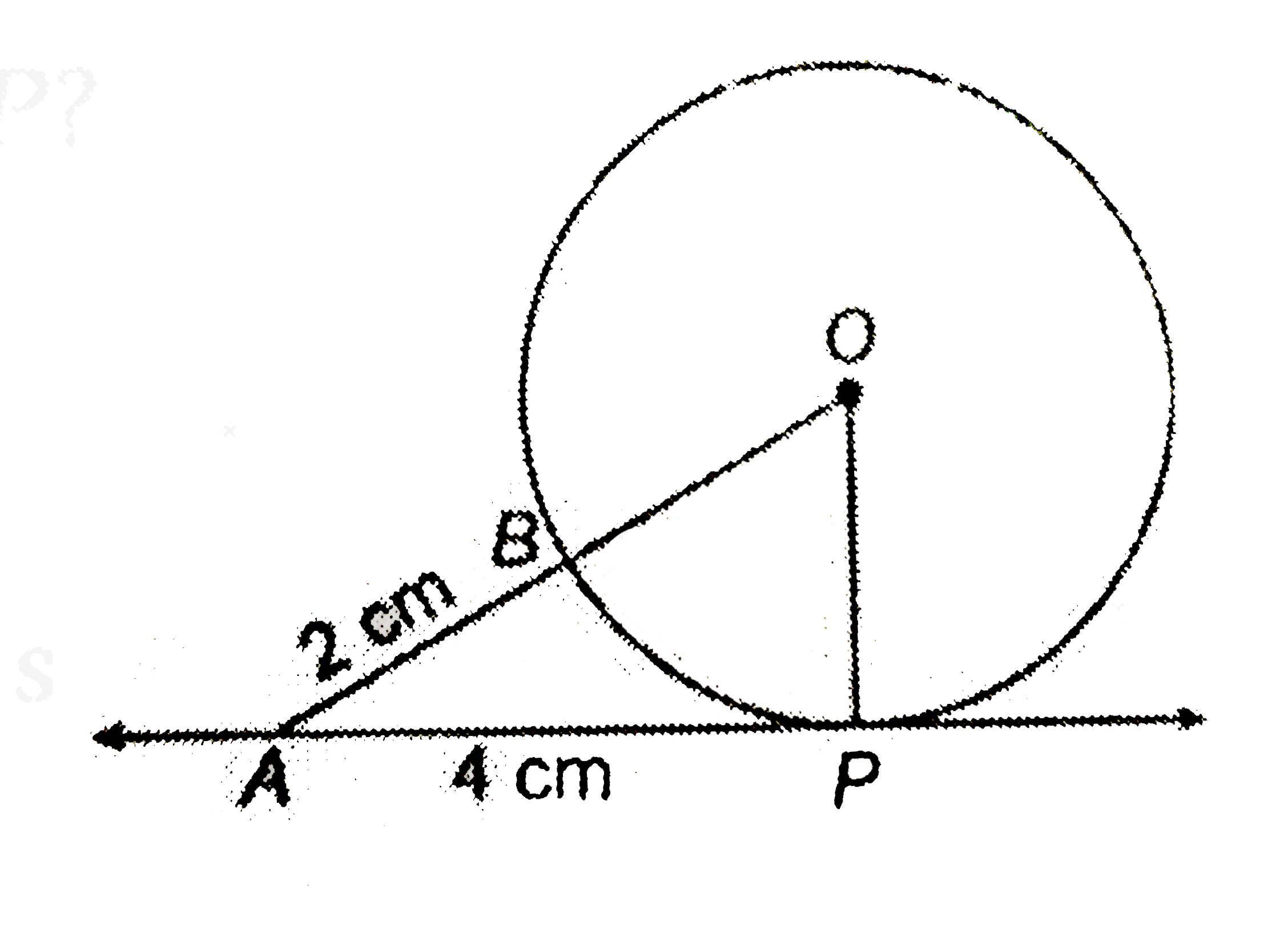
∴ In right △OPA,
OA2=OP2+AP2 (by Pythagoras theorem)
(2+r2)=r2+(4)2
⇒ 4+r2+4r=r2+16
(2+r2)=r2+(4)2
⇒ 4+r2+4r=r2+16
⇒ 4r=12 ⇒ r=3
∴ OP=3cm.
Topper's Solved these Questions
- CIRCLESBook:NAGEEN PRAKASHAN ENGLISHChapter:CIRCLESExercise:Problems From NCERT/exemplar
Explore 11 Videos
- CIRCLESBook:NAGEEN PRAKASHAN ENGLISHChapter:CIRCLESExercise:Exercise
Explore 32 Videos
- ARITHMETIC PROGRESSIONBook:NAGEEN PRAKASHAN ENGLISHChapter:ARITHMETIC PROGRESSIONExercise:Revision Exercise Long Answer Question
Explore 5 Videos
- CO-ORDINATE GEOMETRYBook:NAGEEN PRAKASHAN ENGLISHChapter:CO-ORDINATE GEOMETRYExercise:Revision Exercise Short Answer Questions
Explore 10 Videos
Similar Questions
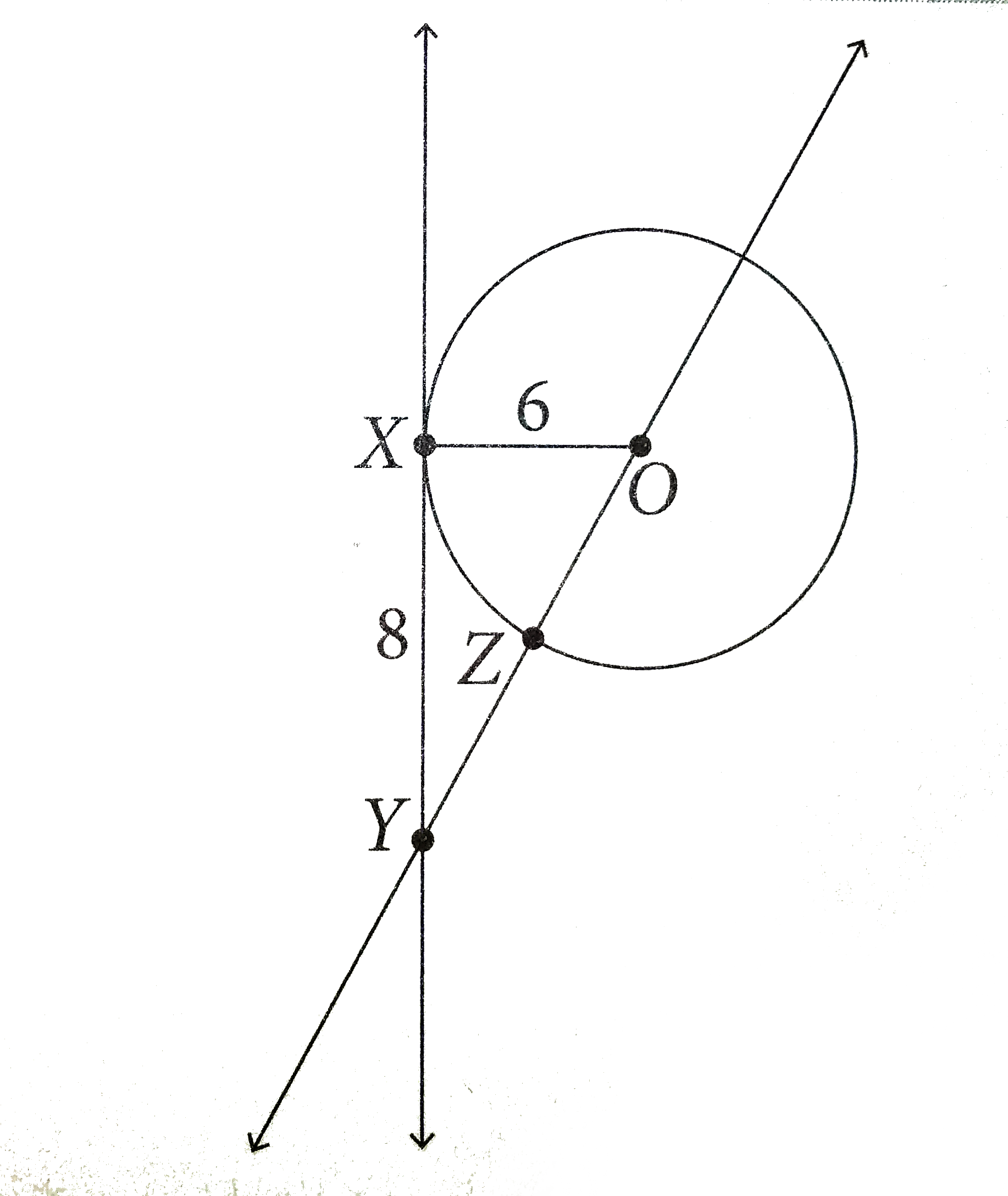
In the figure above, O is the center of the circle, the length of segment XY is 8, and the line passing through point X and Y is tangent to the circle at point X. What is the length of segment ZY?
View Solution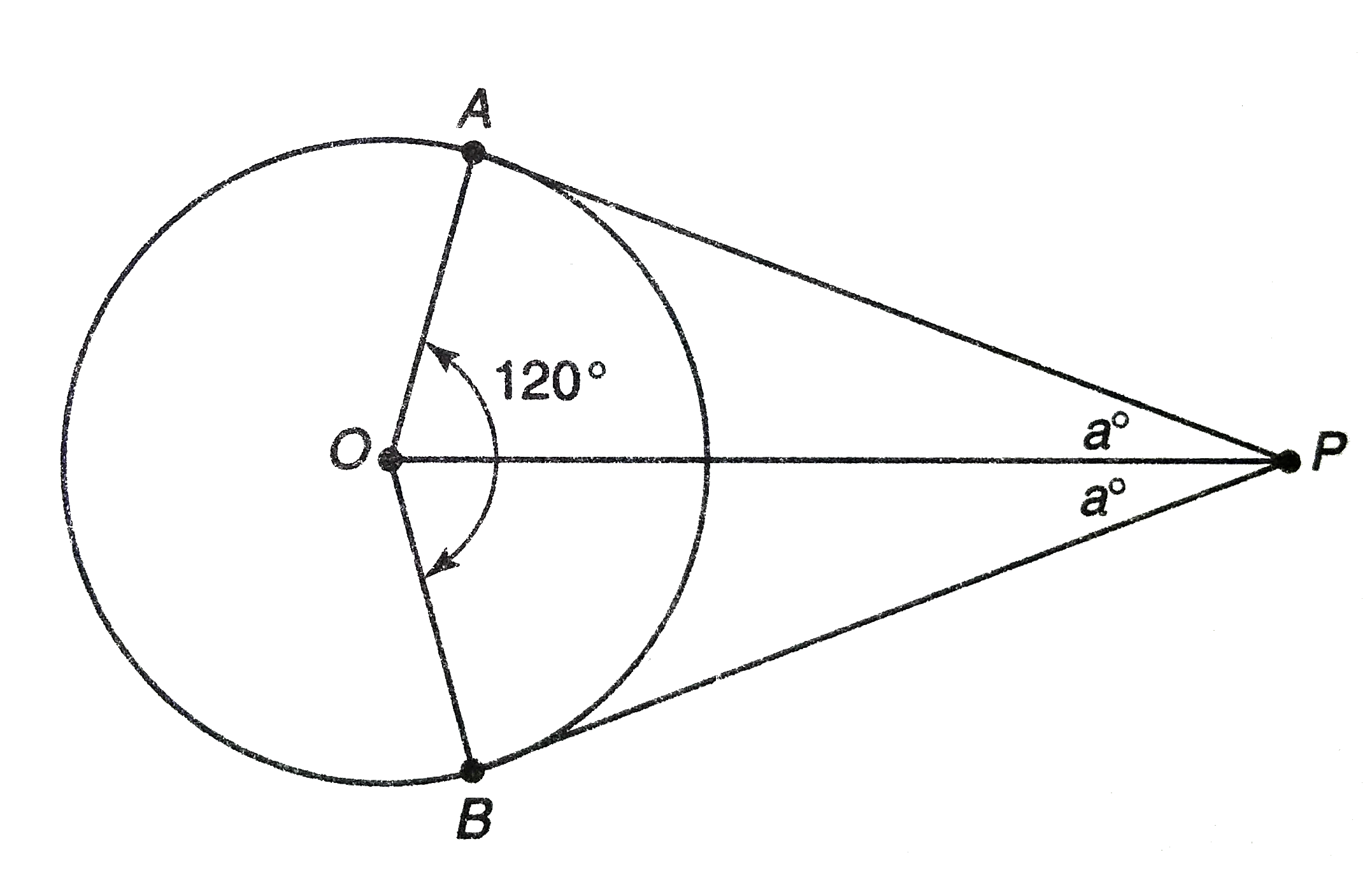
In the figure above, ¯¯¯¯¯¯PA is tangent to circle O at point A, ¯¯¯¯¯¯PB is tangent to circle O at point B. Angle AOB measures 120∘ and OP=4π. What is the length of minor arc AB?
View Solution
Knowledge Check
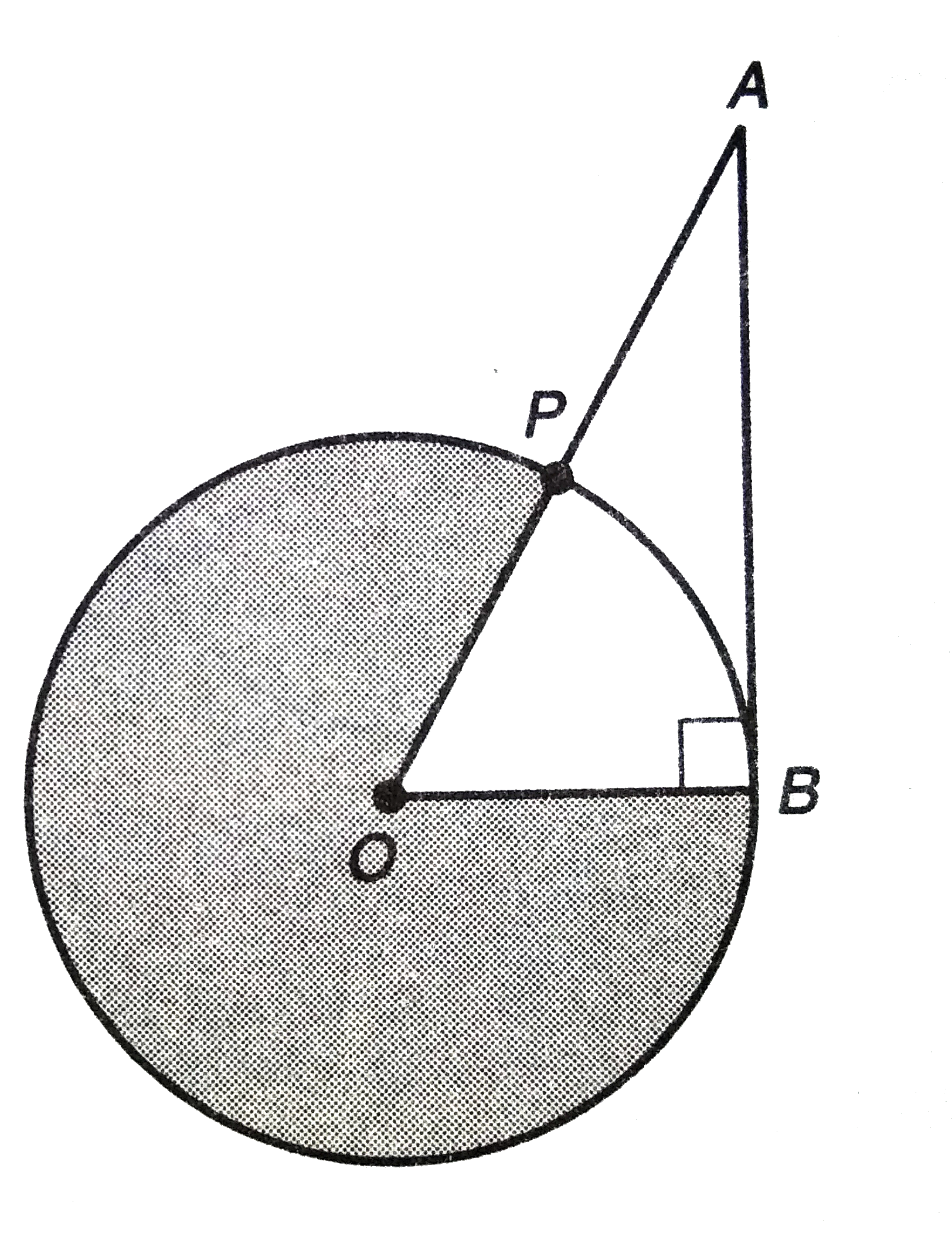
The circle shown above has center O and a radius length of 12. If P is the midpoint of ¯¯¯¯¯¯OAand¯¯¯¯¯¯AB is tangent to circle O at B, what is the area of the shaded region?A81πB96πC120πD128π
Two circles of unequal radii have four common tangents. A transverse common tangent meets the direct common tangents at the points P & Q. If length of direct tangent (between the point of contacts) is 8 then length of PQ is
View SolutionIf the line y=2-x is tangent to the circle S at the point P(1,1) and circle S is orthogonal to the circle x2+y2+2x+2y−2=0 then find the length of tangent drawn from the point (2,2) to the circle S
View Solution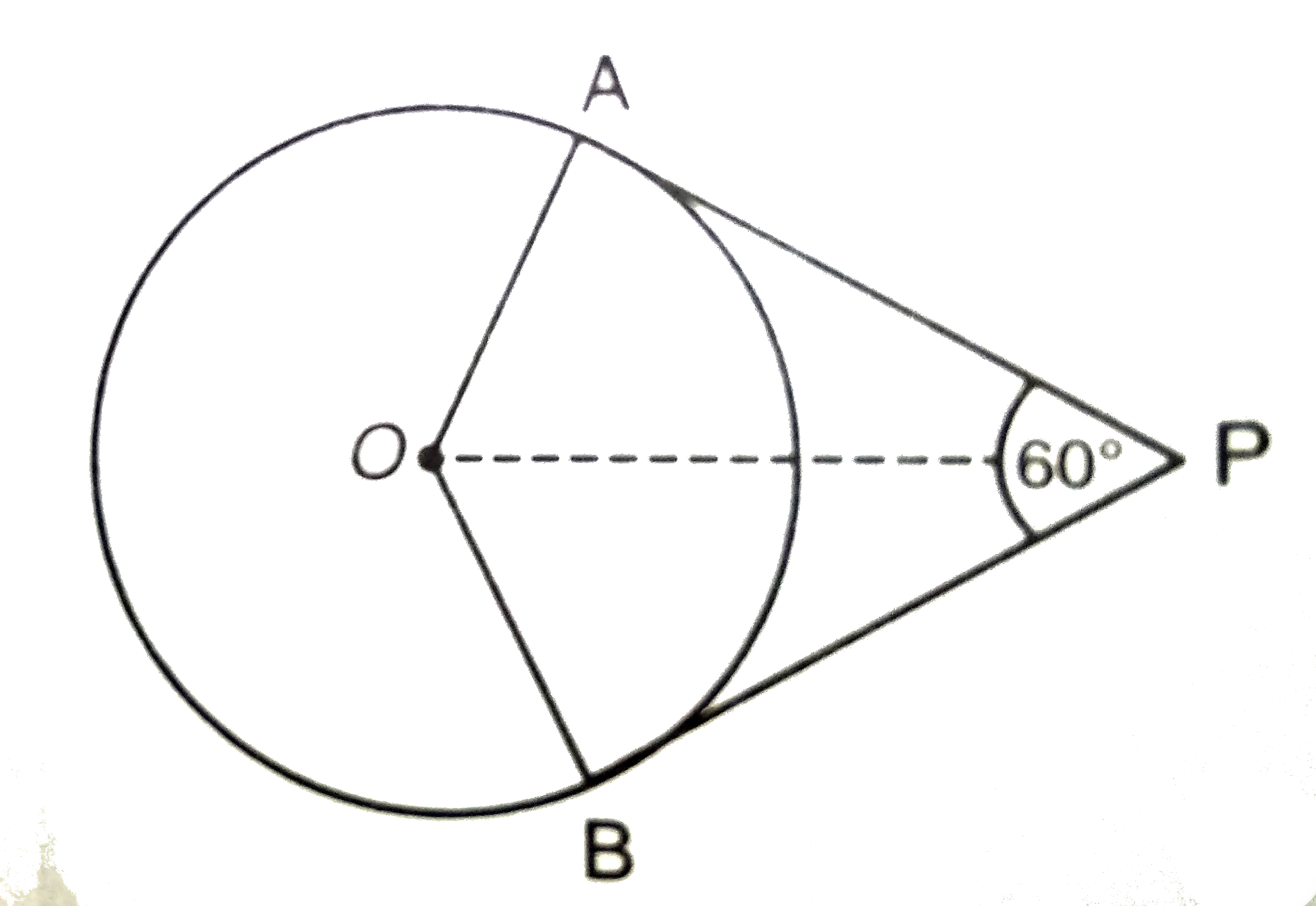
In the figure above, the segments PA and PB are tangent to circle O at points A and B, respectively, and the measure of ∠APB is 60∘. Segment OP is drawn. If OP=14π, what is the length of minor arc AB?
View SolutionPQ is a tangent to a circle with centre O at the point P . If △OPQ is an isosceles triangle, then ∠OQP is equal to :
View SolutionAB is a chord of length 16cm of a circle of radius 10cm. The tangents at A and B intersect at a point P . Find the length of PA .
View SolutionPoint P is the endpoint of vector OP and point Q is the endpoint of vector OQ. When the vectors ¯¯¯¯¯¯OP and ¯¯¯¯¯¯OQ are added, what is the length of the resultant vector ?
View SolutionIn Figure, APB is a tangent to a circle with centre O at point P . If ∠QPB=50∘ , then the measure of ∠POQ is (a)100∘ (b) 120∘ (c) 140∘ (d) 150∘
View Solution

