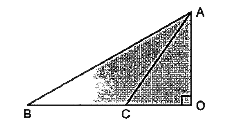
A triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively. Find the sides AB and AC.

Video Solution

Text Solution

Verified by Experts

Given, CD = 6 cm, BD = 8 cm and radius = 4 cm
Join OC, OA and OB.
We know that the tangents drawn from external point are equal in length
$∴ C D = C F = 6 c m$
and $B D = B E = 8 c m$
Let $A F = A E = x c m$
In $△ O C B,$
Area of triangle, $A_{1} = \frac{1}{2} \times B a s e \times H e i g h t = \frac{1}{2} \times C B X X O D$
$= \frac{1}{2} \times 14 \times 4 = 28 c m^{2}$
In $△ O C A,$
Area of triangle, $A_{2} = \frac{1}{2} \times A C \times O E = \frac{1}{2} (6 + x) \times 4 = 12 + 2 x$ ltbtgt In $△ O B A,$
Area fo triangle, $A_{3} = \frac{1}{2} \times A B \times O E = \frac{1}{2} (8 + x) \times 4 = 16 + 2 x$
Now, semiperimeters of triangle $A B C = \frac{1}{2} (A B + B C + C A)$ ltvrgt $s = \frac{1}{2} (x + 6 + 14 + 8 + x) = 14 + x$
Now, area of $△ A B C = A_{1} + A_{2} + A_{3}$
$= 28 + (12 + 2 x) + (16 + 2 x)$
$= 56 + 4 x ... (1)$
Using Heron's formula,
Area of $△ A B C = \sqrt{s (s - a) (s - b) (s - c)}$
$= \sqrt{(14 + x) (14 + x - 14) (14 + x - x - 6) (14 + x - x - 8)}$
$= \sqrt{(14 + x) (x) (8) (6)} = \sqrt{(14 + x) 48 x} ... (2)$
$∴$ From Eqs. (1) and (2), we get
$\sqrt{(14 + x) 48 x} = 56 + 4 x$
On squaring both sides,
$(14 + x) 48 x = 4^{2} {(14 + x)}^{2} \Rightarrow 3 x = 14 + x$
$\Rightarrow 2 x = 14 \Rightarrow x = 7$
$∴$ Length $A C = 6 + X = 6 + 7 = 13 c m$
Length of $A B = 8 + x = 8 + 7 = 15 c m$

Updated on:21/07/2023

|

Class 10 MATHS CIRCLES

Topper's Solved these Questions

Similar Questions

NAGEEN PRAKASHAN ENGLISH-CIRCLES-Problems From NCERT/exemplar

Home
Ask Doubt
Profile