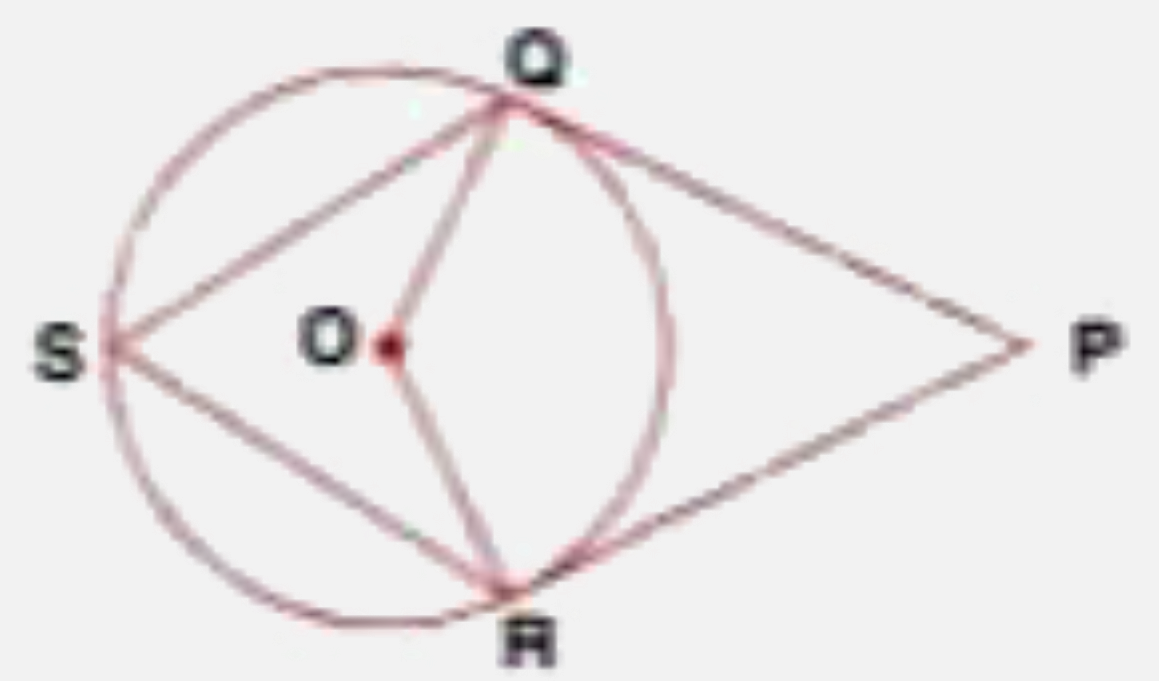
In figure, tangents PQ and PR are drawn to a circle such that ∠RPQ=30∘. A chord RS is drawn parallel to the tangent PQ. Find the ∠RQS.
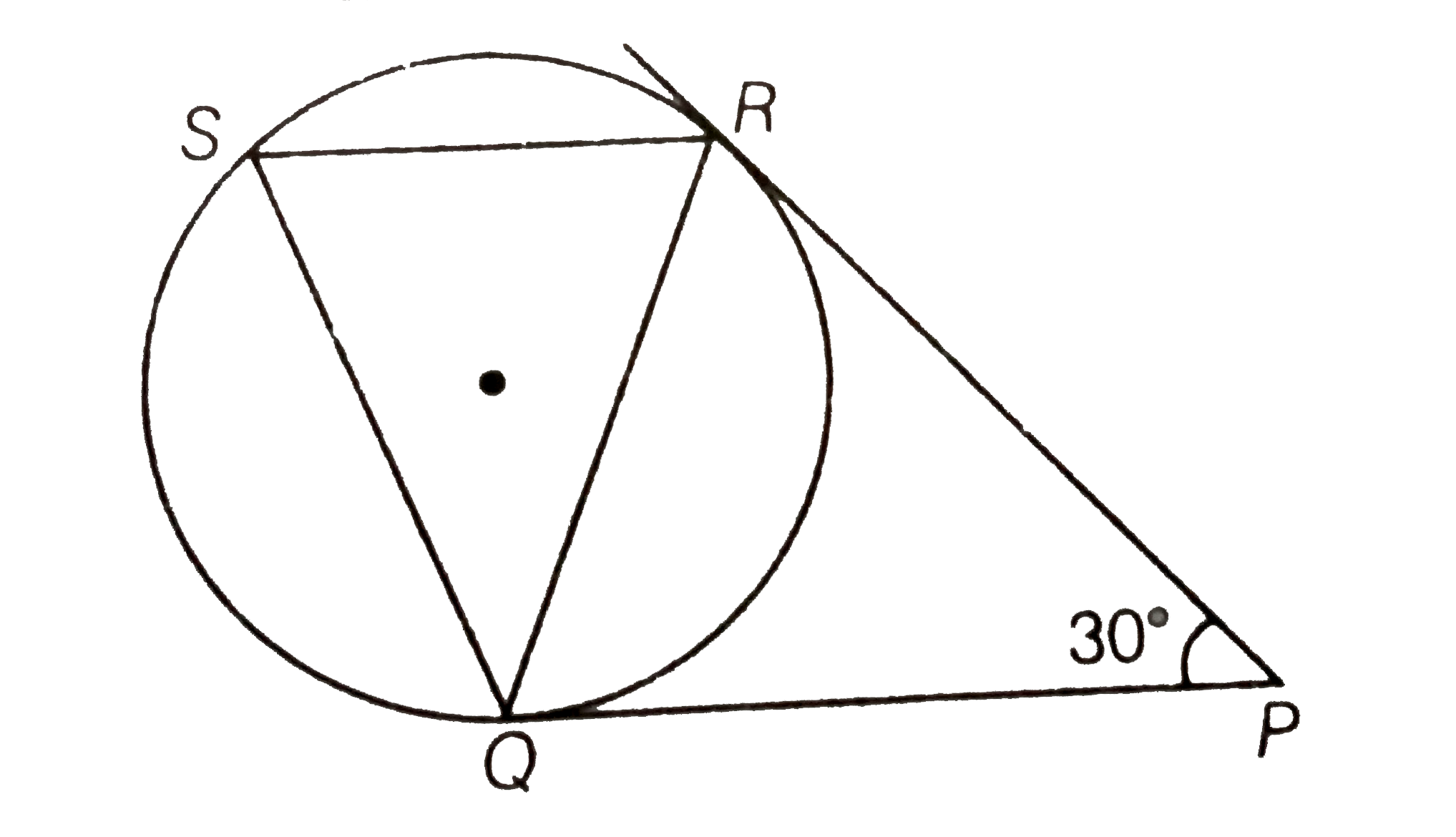
Since, PQ and PR are the tangents to a circle from an external point P.
∴ PQ=PR
⇒ ∠PRQ=∠PQR (angles opposite to equal sides are equal)
In △PQR
∠PQR+∠PRQ+∠QPR=180∘
⇒ ∠PQR+∠PQR+30∘=180∘
⇒ 2∠PQR=150∘ ⇒ ∠75∘
Again SR∣∣QP
∴ SRQ=RQP=75∘
Thus, PQR=QSR=75∘ (by alternate segment theorem)
In △QRS,
∠QRS+∠RSQ+∠SQR=180∘
∠SQR=180∘−75∘−75∘
⇒ ∠RQS=30∘
Topper's Solved these Questions
- CIRCLESBook:NAGEEN PRAKASHAN ENGLISHChapter:CIRCLESExercise:Exercise
Explore 32 Videos
- CIRCLESBook:NAGEEN PRAKASHAN ENGLISHChapter:CIRCLESExercise:Revision Exercise Very Short Answer Question
Explore 7 Videos
- CIRCLESBook:NAGEEN PRAKASHAN ENGLISHChapter:CIRCLESExercise:Long Answer Questions
Explore 2 Videos
- ARITHMETIC PROGRESSIONBook:NAGEEN PRAKASHAN ENGLISHChapter:ARITHMETIC PROGRESSIONExercise:Revision Exercise Long Answer Question
Explore 5 Videos
- CO-ORDINATE GEOMETRYBook:NAGEEN PRAKASHAN ENGLISHChapter:CO-ORDINATE GEOMETRYExercise:Revision Exercise Short Answer Questions
Explore 10 Videos
Similar Questions
In the given figure, tangents PQ and PR are drawn to a circle such that angle RPQ = 30°. A chord RS is drawn parallel to the tangent PQ. Find the angle RQS.
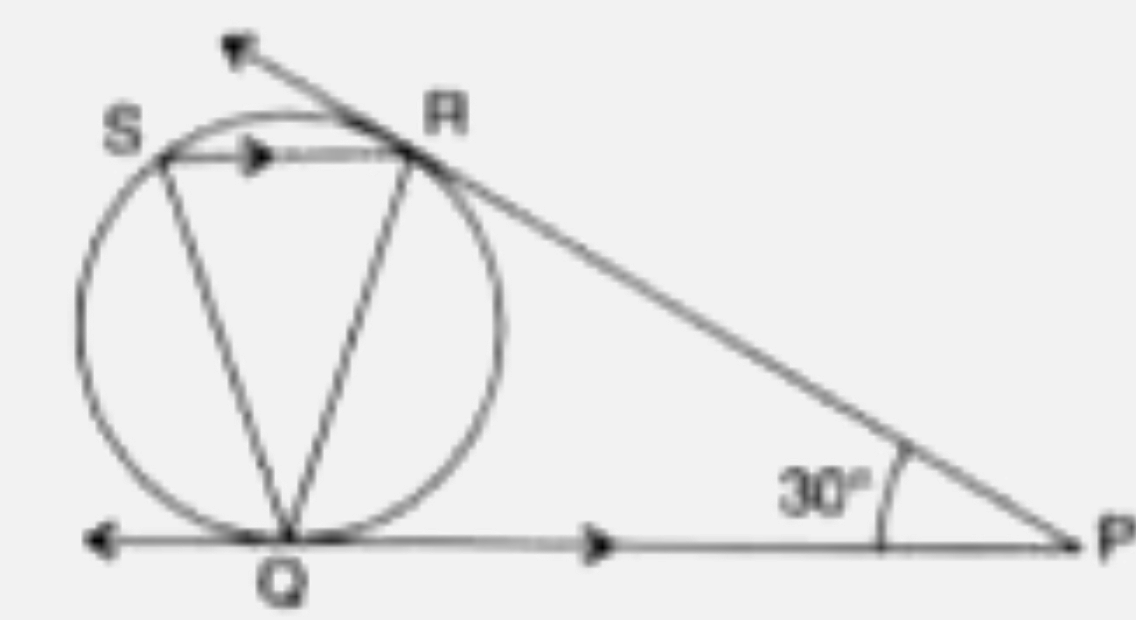
View SolutionIn Figure, if tangents PAandPB are drawn to a circle such that ∠APB=300 and chord AC is drawn parallel to the tangent PB, then ∠ABC= (a)600 (b)900 (c)300 (d) None of these
View SolutionIn the given figure, two tangents PQ and PR are drawn to a circle with centre O from an external point P, Prove that ∠QPR=2∠OQR.
View SolutionIn the given figure, two tangents PQ and PR are drawn to a circle with centre C from an external point P, Prove that ∠QPR=2∠OQR.
View SolutionIf Figure-1, from an external point P, two tangents PQ and PR are drawn to a circle of radius 4 cm with centre O. if ∠QPR=90∘, then length of PQ is
View SolutionIn figure, From an external point P, Two tangents PQ and PR are drawn to a circle of radius 4 cm with centre O . If ∠QPR=90∘ then length of PQ is
View SolutionIn the figure-3, from an external point P, two tangents PQ and PR are drawn to a circle of the radius 4 cm with centre O. If ∠ QPR = 90∘, then length of PQ is
View SolutionIn the following figure PQ and PR are tangents to the circle with the centre O. If ∠QPR=60∘ calculate
(i)∠QOR
(ii) ∠OQR
(iii) ∠QSR
View SolutionIn the given circle if Figure-1, number of tangents parallel to tangents PQ is

View SolutionIn the given circle if Figure-1, number of tangents parallel to tangents PQ is

View Solution

