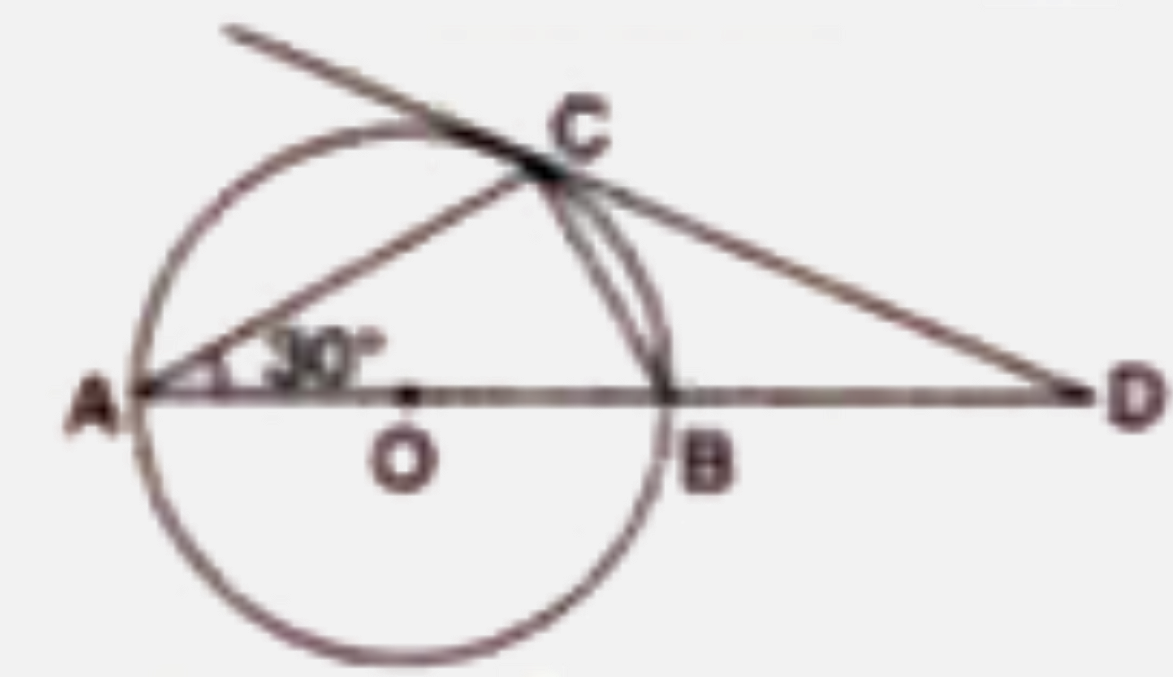
AB is a diameter and AC is a chord of a circle with centre with centre O such that $∠ B A C = 30^{\circ}$ . The tangent at C intersects extended AB at a point D. Prove that BC=BD.

Video Solution

Text Solution

Verified by Experts

True.
CD is a tangent at contact point C. AOB is diameter which meets tangent produced at D.
Chord AC makes $∠ A = 30^{\circ}$ with diameter AB.
To Prove : $B D - B C$
Proof : In $△ O A C,$
$O A = O C = r$ (radii of same dircle)
$∠ 1 = ∠ A$ (angles opposite to equal sides are equal)
$\Rightarrow ∠ 1 = 30^{\circ} (∵ ∠ A = 30^{\circ})$
Exterior $∠ B O C = ∠ 2 = ∠ 1 + ∠ A = (30^{\circ} + 30^{\circ}) = 60^{\circ}$
Now, in $△ O C B,$
$O B = O C$ (radii of same circle)
$∴ ∠ 3 = ∠ 4$ (angles opposite to equal sides are equal)
$∠ 3 + ∠ 4 + ∠ C O B = 180^{\circ}$
$\Rightarrow ∠ 3 + ∠ 3 + 60^{\circ} = 180^{\circ}$ (angle sum property of triangle)
$\Rightarrow 2 ∠ 3 = 180^{\circ} - 60^{\circ} = 120^{\circ}$
$\Rightarrow ∠ 3 = 60^{\circ} = ∠ 4$
$\Rightarrow ∠ 6 + ∠ 4 = 180^{\circ}$ (linear pair axiom)
$\Rightarrow ∠ 6 = 180^{\circ} - ∠ 4 = 180^{\circ} - 60^{\circ}$
$\Rightarrow ∠ 6 = 120^{\circ}$
$∴$ Tangent CD and radius CO are at contact point C.
$∴ ∠ O C D = 90^{\circ}$
(radius through point of contact is perpendicular to the tangent )
$\Rightarrow ∠ 3 + ∠ 5 = 90^{\circ} \Rightarrow 60^{\circ} + ∠ 5 = 90^{\circ}$
$\Rightarrow ∠ 5 = 30^{\circ}$
Now, in $△ B C D,$
$∴ ∠ 5 + ∠ 6 + ∠ D = 180^{\circ}$ (angle sum property)
$\Rightarrow 120^{\circ} + 30^{\circ} + ∠ D = 180^{\circ} \Rightarrow ∠ D = 30^{\circ}$
Since, $∠ C = ∠ D = 30^{\circ} .$
Hence, $B C = B D$ (sides opposite to equal angles)
Hence Proved.

Updated on:21/07/2023

|

Class 10 MATHS CIRCLES

Topper's Solved these Questions

Similar Questions

NAGEEN PRAKASHAN ENGLISH-CIRCLES-Problems From NCERT/exemplar

Home
Ask Doubt
Profile